3. Пусть объем перевозимого через поставщиков груза составляет 80 единиц и надо составить оптимальный план перевозок. Тогда выделяется «Дополнительно заданный объем перевозок», нажимается ОК, что приводит к окну ввода:
Ввод 80, и нажатие ОК, дают:
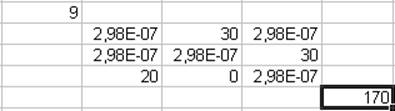
4. Нахождение оптимального плана перевозок, при котором весь груз со второго склада вывезен. Выделяется «Приоритет», нажимается ОК, что приводит к окну ввода:
Ввод 2, и нажатие ОК, дают:
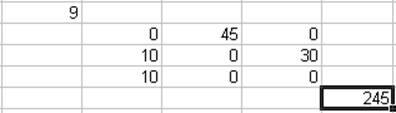
5. Нахождение оптимального плана перевозок, при котором со второго и третьего складов вывозятся равные объемы груза. Выделяется модель «Паритет», нажимается ОК, что приводит к окну ввода:
Ввод 2, и нажатие ОК, приводят к следующему окну:
Ввод 3, и нажатие ОК, дают оптимальный план:
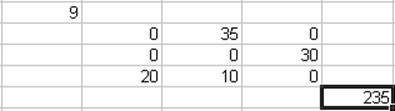
Рис. 3.25
4. Задача коммивояжера
Одна из наиболее популярных оптимизационных задач, состоящая в
нахождении такого маршрута объезда n городов (по одному
разу), при заданных расстояниях ![]() ,
между ними, который имеет минимальную длину. Аналитически решается методом
«ветвей и границ», требующим больших вычислений.
,
между ними, который имеет минимальную длину. Аналитически решается методом
«ветвей и границ», требующим больших вычислений.
Математическая постановка в
булевых (альтернативных) переменных ![]() ,
для которых
,
для которых ![]() ,
если путь из пункта
,
если путь из пункта ![]() в пункт
в пункт ![]() входит в
оптимальный маршрут, и
входит в
оптимальный маршрут, и ![]() , если не
входит, имеет вид:
, если не
входит, имеет вид:
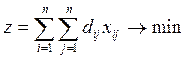 , (11)
, (11)
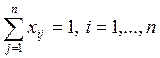 ,
, 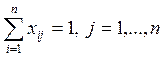 ,
, ![]() , (12)
, (12)
непрерывность маршрута обеспечивается
введением дополнительных независимых переменных ![]() , связанных с
, связанных с ![]() условиями
условиями
![]() (13)
(13)
Из первого пункта
можно двигаться в любом направлении, поэтому в (13) индекс ![]() . Если переменным
. Если переменным ![]() присвоить значения,
равные номерам пунктов, через которые проходит оптимальный маршрут, то условия
(13) будут выполнены. Поэтому более жесткие ограничения на переменные
присвоить значения,
равные номерам пунктов, через которые проходит оптимальный маршрут, то условия
(13) будут выполнены. Поэтому более жесткие ограничения на переменные ![]() :
:
![]() (14)
(14)
Тестирование
Матрица расстояний:
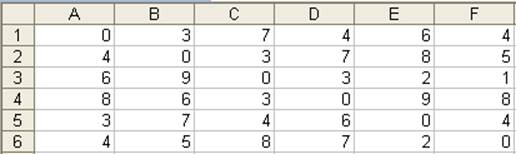
Рис. 3.27
Результаты:
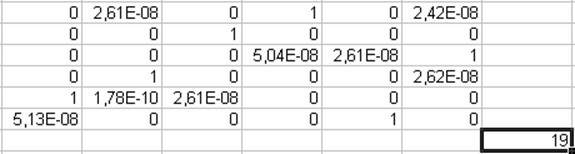 Рис. 3.28
Рис. 3.28
Оптимальный маршрут: ![]() . Минимальная длина
пути равна 19.
. Минимальная длина
пути равна 19.
5. Матричная игра
Платежная функция
игры, заданной матрицей ![]() ,
,
![]() , имеет вид:
, имеет вид:
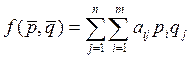 ,
, ![]() ,
, ![]()
Величина V=![]() называется ценой
игры, а стратегии
называется ценой
игры, а стратегии ![]() –
оптимальными, если для всех остальных
–
оптимальными, если для всех остальных ![]() выполняется:
выполняется:
![]()
В силу последнего неравенства
стратегия ![]() есть решение
задачи линейного программирования:
есть решение
задачи линейного программирования:
![]() , (15)
, (15)
![]() (16)
(16)
Обычно, что в компьютерных технологиях лишнее,
ограничения делят на величину ![]() и
переходят к поиску минимума целевой функции
и
переходят к поиску минимума целевой функции ![]() . Стратегия
. Стратегия ![]() находится
аналогично:
находится
аналогично:
![]() (17)
(17)
![]() (18)
(18)
Макрос возвращает по платежной матрице произвольных размерностей, больших 1, оптимальные частоты игроков.
Тестирование
Платежнаяматрица:
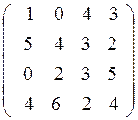
Запуск макроса открывает диалоговое окно:
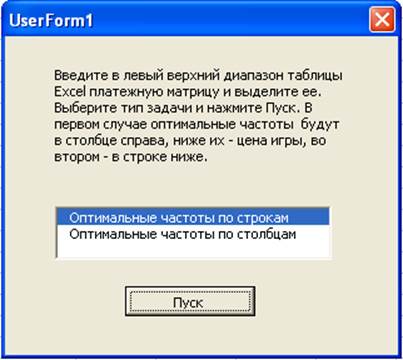
Вводится платежная матрица:
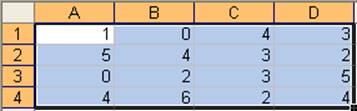
Нажатие кнопки Пуск дает частоты оптимальных стратегий первого игрока и цену игры:
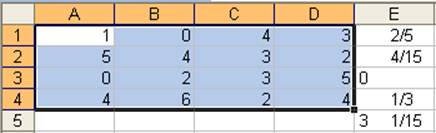
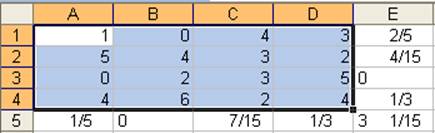
Выделение в диалоговом окне второй строки, и нажатие кнопки Пуск, возвращает оптимальные частоты другого игрока:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.