Если теперь предположить, что нагрузка линии отсутствует, т.е. приемный конец разомкнут (l2. = 0), то в предположении неизменности величины U2ф векторная диаграмма примет вид, показанный на рис. 4.10, в. Ее сопоставление с двумя предыдущими диаграммами показывает, что:
— для поддержания в режиме холостого хода напряжения в конце линии на уровне, соответствующем нормальным режимам, напряжение в начале линии должно быть значительно снижено (U1ф < U2ф)',
— ток в начале линии имеет практически чисто емкостный характер (Ф1 = 90°), опережая напряжения U2ф и u\ф; при этом он направлен в сторону противоположную по отношению к току в режиме максимальной нагрузки, т.е. в сторону источника питания, а не потребителя.
Подытоживая рассмотрение векторых диаграмм рис. 4.10, следует подчеркнуть, что они отражают частное, хотя и довольно характерное для ВЛ 110—220 кВ, соотношение параметров продольной ветви схемы замещения (гд и Дд) и демонстрируют качественно относительное влияние на параметры режима линии ее зарядного тока. Более подробно взаимоотношения параметров собственно линии и параметров ее режима будут проанализированы в § 4.3 г.
Определение параметров установившегося режима линии
Как уже упоминалось выше, задачей расчета установившегося ре жима является определение мощностей и токов во всех ветвях и напряжений в узлах схемы замещения. Применительно к линии электро-
|
передачи должны быть определены мощности и напряжения, показанные на рис. 4.11. Прежде чем приступить к рассмотрен! алгоритма расчета режима линии, напомни что для определения полной мощности фазе цепи (5ф) могут быть использованы два подхода. Согласно первому ив них, мощность определяется как произведение |
|
|
|
Рис. 4.11. Потоки мощности в схеме замещения линии электропередачи |
• «а тока на сопряженный комплекс напряжения, т.е. Sф(1) = IUф. При втором подходе мощность определяется как произведение сопряженного комплекса
тока на напряжение, т.е. Sф(2) = 1Uф.
Считая, что в обоих случаях вектор фазного напряжения направлен по действительной оси комплексной плоскости и что ток отстает от напряжения, т.е. I = la— jIr получим
|
(4.114) (4.115) |
![]()
где Рф, qф) — соответственно активная и реактивная мощности фазы.
Таким образом, рассматриваемые случаи определения Sф отличаются лишь противоположными знаками перед мнимой составляющей полной мощности. Если подходить с абстрактных позиций, то выбор того или иного подхода не имеет принципиального значения. Однако при анализе электроэнергетических систем целесообразно выбрать тот подход, который в наибольшей степени соответствует реальным физическим соотношениям активной и реактивной мощностей, протекающих в ее элементах. С этой точки зрения второй подход предпочтительнее, так как одинаковость знаков перед активной и реактивной мощностями [см. формулу (4.115)] соответствует реальной роли электрических станций в системе как основных источников и активной, и реактивной мощностей. Естественно при этом в качестве положительного направления потока активной мощности принять направление от источника питания к потребителю. В большинстве режимов такое же направление имеет и поток реактивной мощности, поэтому одинаковость знаков Рф и < Qф отвечает физической картине явления.
Итак, условимся, что в дальнейшем везде будет использоваться определение полной мощности как произведения сопряженного комплекса тока на прямой комплекс напряжения. В соответствии с этим мощность трех фаз ("трехфазная" мощность)
![]()
где U — линейное (междуфазное) напряжение.
Расчет режима линии по заданным параметрам на ее приемном конце. Начиная рассмотрение алгоритма расчета режима линии, примем, что в качестве известных исходных данных выступают параметры режима на приемном конце линии, т.е. заданы мощность S2 = P2 - jQ2 и модуль линейного напряжения U2 которое будем считать совпадающим с действительной осью комплексной плоскости (U2 = U2). Итак, приступим к определению потоков мощности в схеме замещения, показанной на рис. 4.11, полагая, как и ранее, что потерями на корону можно пренебречь.
119




S2 = S12 - Sc2 = P1 -dP12 + j(Q1 +Qc1 -dQ12 + Qc2) =
P2 + jQ2
|
(4.138) |
Таким образом,
|
(4.139) (4.140) (4.141) |
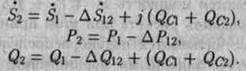
|
Рис. 4.12. Векторные диаграммы мощностей |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.