Таким образом, все рассмотренные варианты характерны тем, что при выполнении расчетов напряжение задано по концам линии на шинах двух источников питания.
Заметим, что если напряжение задано только с одного конца, то, несмотря на наличие двух источников питания, такая сеть равносильна случаю радиальной сети (см. рис. 6.2, г) и ее расчет проводится по правилам, изложенным в главе 5.
Перейдем теперь к рассмотрению методики расчета линии с двухсторонним питанием.
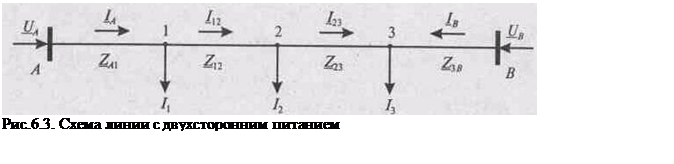 |
Известны напряжения на шинах источников питания UA и UB. Предположим, что направление токов в ветвях, как указано на схеме. Узел 3 получает питание с двух сторон. Тогда напряжение в узле 3 можно записать через напряжение в узле А и падение напряжения от

где Z — сопротивление участков линии между двумя источниками питания; Ii, — ток нагрузки в i-м узле; ZiB — сопротивление от i-го узла до источника В.
Аналогичным образом для тока источника питания В можно записать:
|
|
(6.5) |
где ZiA — сопротивление участков линии от i-го узла до источника питания А.
Первый член в выражении (6.4) представляет собой сквозной уравнительный ток:
|
(6.6) |
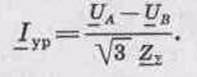
Он обусловлен разностью напряжений источников питания и полным сопротивлением всей сети. Его значение не зависит от величины и места расположения нагрузок.
Второй член в выражении (6.4) обусловлен только нагрузками в узлах и соотношением сопротивлений на отдельных участках сети.
Если нагрузки в узлах выражены мощностями, то, умножив левые и правые части выражений (6.4) и (6.5) на \/3 Uном, можно получить выражения для мощностей, подаваемых в рассматриваемую сеть от источников питания:
|
(6.7) (6.8) |
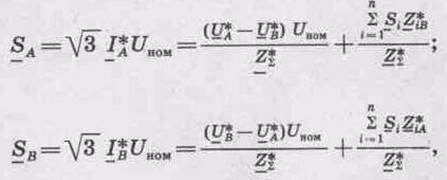
где Si, — заданная мощность в i-м узле; Uном — номинальное напряжение сети.
Так, для сети, приведенной на рис. 6.3, мощность источника питания А
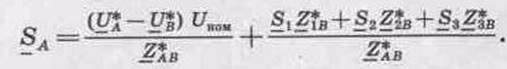
Первый член в выражении (6.7) представляет собой сквозную уравнительную мощность, протекающую по всей сети от источника А до источника питания В:
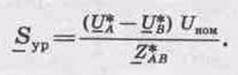
Переход от строгих выражений для токов (6.4), (6.5) к выражениям для мощностей (6.7), (6.8) осуществлен с допущением, что напряжения во всех точках сети одинаковы. В результате расчет по выражениям (6.7), (6.8) позволяет найти потоки мощности и их направления на участках сети без учета потерь мощности. Зная поток мощности на одном из головных участков сети, на основании первого закона Кирхгофа применительно к каждому узлу сети легко найти потоки мощности на всех остальных участках. Так, если известна мощность Sa на участке А1 (см. рис. 6.3), то мощность на участке 12
![]()
|
(6.9) |
Для проверки результатов расчета рекомендуется находить мощности, выходящие из обоих источников питания. Сумма этих мощностей должна быть равна сумме мощностей нагрузок в узлах:
![]()
Пусть в результате расчета направления потоков мощностей по участкам оказались такими, как показано на рис. 6.4, а. Здесь узел 2 питается с двух сторон. Узел сети, нагрузка которого питается с двух сторон, называется точкой потокораздела или точкой токораздела. Точку потокораздела активных мощностей на схемах обычно обозначают через V, а реактивных — через V. На рис. 6.4, а обе эти точки совпадают в узле 2. Здесь сплошными стрелками показаны направления активных мощностей, а пунктирными — реактивных мощностей.
На рис. 6.4, б показан случай, когда точки потокораздела не совпадают. Активные мощности здесь сходятся в узле 2, а реактивные — в узле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.