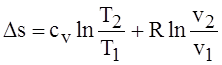 ;
(1.53)
;
(1.53)
или
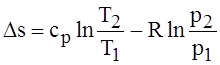 ; (1.54)
; (1.54)
Все исследуемые в дальнейшем процессы принимаются равновесными и обратимыми.
Рассмотрим основные термодинамические процессы, протекающие в идеальном газе и имеющие широкое применение в теплотехнике.
1.9.1.Изохорный процесс
По определению изохорным называется процесс, протекающий при постоянном объеме. Уравнение процесса (изохора) v =const.
Найдем связь между параметрами состояния газа в изохорном процессе 1-2, используя уравнение Клапейрона. Для начального состояния p1v=RT1, для конечного состояния p2v=RT2. Отсюда получаем зависимость p2/p1=T2/T1, называемую законом Шарля: давление в системе в изохорном процессе пропорционально абсолютной температуре.
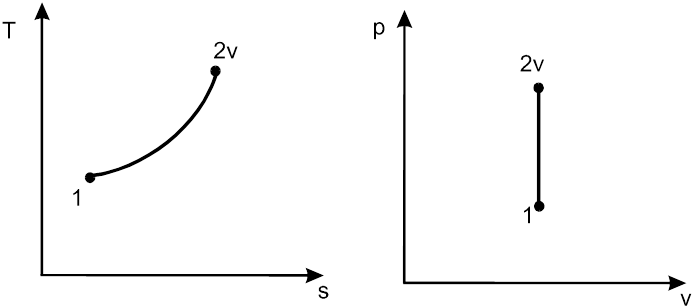
На рис.1.16 представлен изохорный процесс в pv- и Тs-диаграммах.
 |
Работа расширения в изохорном процессе lv = 0, поскольку v1 = v2.
Так как dlv= 0, то из (1.50) следует, что dqv = du, т. е. вся теплота процесса идет на увеличение внутренней энергии газа, и ее можно рассчитать по формуле (1.51):
![]()
![]() .
.
Соответственно изменение энтальпии и энтропии можно получить, исходя из уравнений (1.52) и (1.53):
![]() ;
;
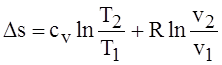 .
.
Отсюда видно, что линия изохорного процесса в Тs-диаграмме (рис.1.16) имеет логарифмический характер.
1.9.2.Изобарный процесс
Процесс, в котором давление остается неизменным, называется изобарным процессом. Уравнение изобары имеет вид р = const. Тогда из уравнения Клапейрона для состояний 1 и 2 следует закон Гей-Люссака:
![]() .
.
Работа процесса р = const
lp = р (v2 – v1) = R(T2 – T1).
Работа lp изобарного процесса в рv-диаграмме изображается площадью прямоугольника 12341 (рис.1.17).
Из (1.50) для теплоты изобарного процесса имеем
![]() ,
,
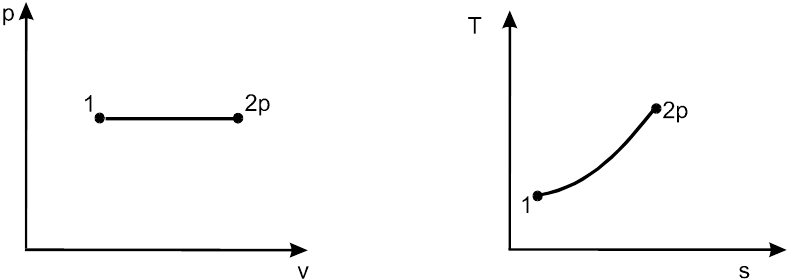 |
Рис. 1.17. Изображение изобарного процесса в рv - и Тs-диаграмме
Для расчета изменения внутренней энергии изобарного процесса имеем
![]() .
.
Поскольку ![]() и
и ![]() , то из первого закона термодинамики
(1.50) следует, что часть теплоты процесса идет на изменение внутренней энергии
газа, а другая часть — на совершение работы изменения объема.
, то из первого закона термодинамики
(1.50) следует, что часть теплоты процесса идет на изменение внутренней энергии
газа, а другая часть — на совершение работы изменения объема.
Из формулы (1.54) получим выражение для расчета энтропии в изобарном процессе
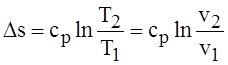 .
.
Энтропия в изобарном процессе в зависимости от температуры изменяется по логарифмическому закону, так же как и в изохорном процессе (см. рис.1.16), но изохора в Тs-диаграмме круче изобары. Это объясняется тем, что cp>cv в формулах для определения Dsv и Dsp.
1.9.3.Изотермический процесс
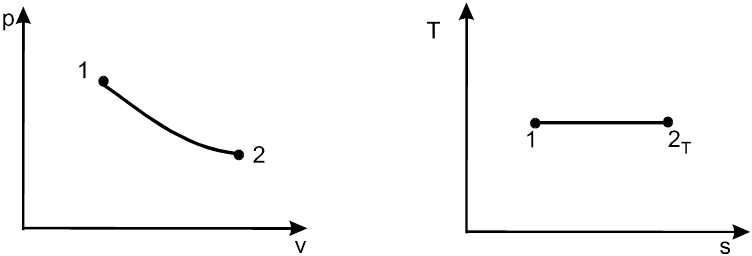
Процесс, в котором температура не меняется, называется изотермическим Т = const. Это значит, что pv=RT=const и p1v1=p2v2. Это уравнение называется законом Бойля — Мариотта, и из него следует, что в изотермическом процессе давление и объем газа связаны между собой обратно пропорциональной зависимостью. Линия изотермы pv=const в рv-диаграмме имеет вид гиперболы.
 |
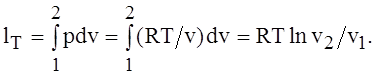
С учётом закона Бойля — Мариотта запишем это выражение в другом виде:
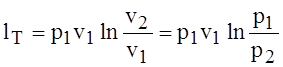 .
.
Поскольку в изотермическом процессе ∆T = 0, то ∆u = 0 и ∆h = 0 и по первому закону термодинамики (1.50)
![]() или
или ![]()
т. е. вся теплота изотермического процесса преобразуется в работу процесса, а внутренняя энергия газа не меняется. Из этого следует также, что работу изотермического процесса можно рассчитать по формуле
![]()
Так как в изотермическом процессе ∆u = ∆h = 0, то, следовательно,
u = const и h = const.
Изменение энтропии согласно (1.53) и (1.54) выразится как
![]()
Рис.1.18 наглядно иллюстрирует изотермический процесс в рv- и Тs-диаграммах.
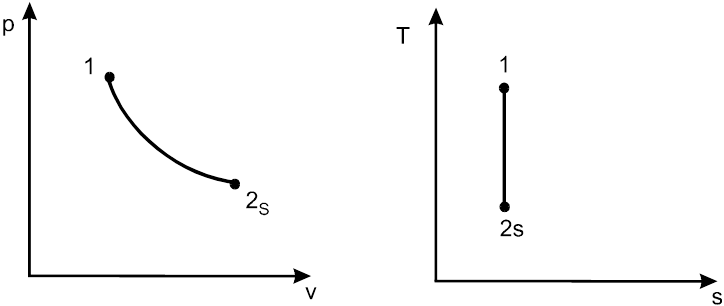 |
Рис. 1.19. Адиабатный процесс в рv- и Тs-диаграммах
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.