Изохорный процесс. Изотермический процесс. Адиабатное истечение газов и паров из сопел, страница 2

Найдем уравнение адиабатного процесса. Для этого запишем уравнение первого закона термодинамики (1.50) с учетом (1.21) при dq = 0:

Разделив первое уравнение на второе, после сокращения на dT получим дифференциальное уравнение адиабаты 

Используя ранее введенное обозначение показателя адиабаты , после разделения переменных и интегрирования имеем

, или

Отсюда следует связь между параметрами состояния в адиабатном процессе

Соответственно уравнение адиабатного процесса для любых р и v, называемое адиабатой Пуассона, имеет вид

                                               (1.55)

Используя уравнение состояния идеального газа (1.48), можно получить соотношения между параметрами состояния в адиабатном процессе:                           

Из рис.1.2 следует, что кривая адиабатного процесса идет круче, чем изотерма, за счет показателя степени k > 1.

Удельная работа в равновесном адиабатном процессе производится только за счет изменения внутренней энергии газа и при с_v = const равна:

Если подставить с_v из (1.24), то получим другие формулы для расчета l_s

или, с учетом уравнения состояния идеального газа (1.48):

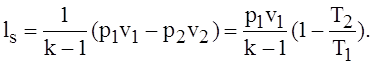                       (1.56)

Используя соотношения параметров в адиабатном процессе, запишем еще два выражения для вычисления удельной работы адиабатного процесса:

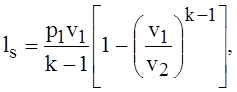
или 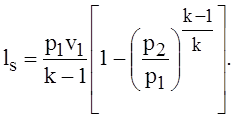                                                                           (1.57)

Выражения (1.56) и (1.57) получены при k=const. В случае, если коэффициент адиабаты зависит от температуры, то в практике расчетов используется его среднее значение:

По определению обратимого адиабатного процесса теплота q_s = 0.

Изменение внутренней энергии обратимого адиабатного процесса ∆u = -l_s, а изменение энтропии ∆s = 0. Изменение же энтальпии можно рассчитать по формуле (1.52):

_.

С помощью несложных преобразований можно найти связь между изменением энтальпии в адиабатном процессе и работой. Используя формулу (1.24), получаем

а с учетом ∆u = -l_s получаем окончательно, что

1.9.5.Политропные процессы

Это обратимые термодинамические процессы, описываемые уравнением  с постоянным и произвольным значением показателя политропы n  ().

Политропный процесс является процессом, обобщающим все рассмотренные выше процессы, т.е. n=0 соответствует изобарному процессу,  n=1 - изотермическому процессу, n = k - адиабатному и n = ±  - изохорному процессам.

Политропные процессы используются при анализе процессов в газовых двигателях, так как часто реальные процессы в них не являются ни адиабатными, ни изотермическими, а занимают промежуточное положение. Поэтому реальные значения n в этих случаях изменяются в пределах от 1 до k.

Уравнения связи для любых двух состояний газа в политропном процессе имеют вид

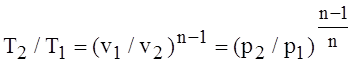   или   .                (1.58)

Обобщив адиабатный процесс (1.56), (1.57) на политропный, с учетом (1.58), запишем аналогичные уравнения для удельной работы:

                (1.59)

или

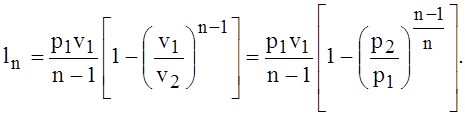                   (1.60)

Теплоту политропного процесса можно определить, используя первый закон термодинамики в виде q_n = ∆u + l_n. Если обозначить через c_n теплоемкость политропного процесса, то, приняв с_n = const, его можно переписать таким образом:

Отсюда теплоемкость политропного процесса

.

и, следовательно, теплота процесса

.

1.10.Адиабатное истечение газов и паров из сопел

Соплом называется канал, специально спрофилированный для увеличения скорости газов до заданного значения и в заданном направлении. Сопла имеют суживающийся или комбинированный профиль.

Рассмотрим случай обратимого адиабатного истечения газа из неограниченного сосуда через суживающееся сопло. Из-за большой скорости протекания процесса истечения газ не успевает обмениваться теплотой с внешней средой, и поэтому q = 0.

Примем следующие исходные и конечные параметры газа: в неограниченном сосуде p₀, v₀, Т₀, с₀ и на срезе сопла р₁, v₁, T₁, с₁, причем р₀ > р₁ (рис.1.20). Площадь выходного сечения F₁.

Рис.1.20. Схема истечения газа

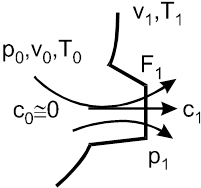При принятых условиях имеем III частный случай первого закона термодинамики для потока и из уравнения (1.18) получим формулу теоретической скорости адиабатного истечения газа на выходе  из сопла

, м/с.                                 (1.61)

Обычно с₀<<с_1t, поэтому (1.61) упрощается:

, м/с.                            (1.62)

          Здесь уменьшение энтальпии H_0с =h₀ – h_1t, Дж/кг называется располагаемым теплоперепадом сопла.