Определение площади поверхностей контакта фаз в системах металл-шлак-газ в условиях значительной их деформации методами физического моделирования: Лабораторный практикум, страница 4

Поскольку температуру поверхности жидкости непосредственно измерить нельзя, то ее, как правило, приравнивают к объемной температуре. При реализации обоих методов это вносит дополнительную погрешность в определении площади деформированной поверхности жидкости.

Дополнительную погрешность можно устранить, проводя оба процесса – испарение воды и абсорбцию диоксида углерода – одновременно в одном реакторе в условиях, при которых эндотермический и экзотермический эффекты этих процессов равны, что обеспечивает постоянство и равенство температуры поверхности жидкости объемной температуре.

Условие

                             (15)

позволяет осуществить безградиентную по температуре методику определения площади контакта жидкости со струей газа. Поскольку при этом температура жидкости не меняется в результате продувки, то скорость того или другого процесса необходимо определять по изменению состава раствора или газовой фазы. Расчетная формула для площади контакта фаз при этом несколько усложняется:

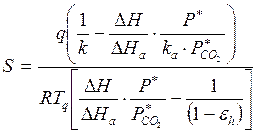                           (16)

здесь  - парциальное давление СО₂ в газовой смеси, при котором выполняется условие (15), в котором  и  - соответственно скорости испарения воды и абсорбции диоксида углерода, моль/с. Величина определяется экспериментально путем изучения зависимости  от  и экстраполяции (интерполяции) ее на значение .

Поскольку точная методика оказывается более трудоемкой, для изучения зависимостей площади контакта фаз от параметров системы и управляющих воздействий на качественном уровне могут быть использованы приближенные методы.

Одна из величин, входящих в расчетные формулы для , а именно теплоемкость системы , может быть определена экспериментально.

Поскольку основу физической модели в обоих вариантах составляет жидкая вода, то добавление к системе с исходной температурой  определенного количества воды  с начальной температурой  позволит по изменению температуры системы оценить ее теплоемкость.

Действительно, составив уравнение теплового баланса в таком процессе

               (17)

находим

,                        (18)

где  - конечная температура системы после смешения основной массы воды  с добавленной, ºС;  - удельная теплоемкость воды, Дж/(кг·К), ≈4200Дж/(кг·К). Учитывая, что теплоемкость системы состоит из эквивалентной теплоемкости «сухой» модели конвертера  и основной массы воды ·, рассчитаем

=-·                              (19)

Порядок выполнения работы

Для нахождения эквивалентной теплоемкости модели конвертера  необходимо: налить в модель конвертера 1л дистиллированной воды и привести модель в вертикальное положение, поднять фурму выше уровня свободной поверхности воды, опустить термометр так, чтобы нижний резервуар термометра был полностью погружен в воду, а сам термометр находился на расстоянии 20...30 мм от оси фурмы и конвертера.

Не включая компрессор, в течение 10 минут через каждую минуту измерять температуру воды в модели, после чего на 11 минуте влить на максимально возможном расстоянии от термометра заранее подогретую до температуры кипения воду объемом 0,1 л и непрерывно перемешивая мешалкой воду, продолжить измерение ее температуры в течение 15 минут. Затем графическим методом определить , а по нему и конечную температуру системы .

По формулам (18) и (19) рассчитывают  и .

После этого по указанию преподавателя еще один или два раза вливают по 0,1 л воды при температуре ее кипения и снова вычисляют  с учетом фактической массы воды , которая с каждым опытом увеличивается на ~0,1 кг.

Затем вычисляют среднюю величину по формуле

                     (20)

где - число определений.

Перед включением компрессора необходимо убедиться в том, что рубильник в лаборатории 626 включен, а вентили 9,10,11 и 12 на передней панели вытяжного шкафа (лаб. 628) установлены в крайнее левое положение.