Определение площади поверхностей контакта фаз в системах металл-шлак-газ в условиях значительной их деформации методами физического моделирования: Лабораторный практикум, страница 3

Для реализации способа вначале несущий газ подают на поверхность жидкости с объемной скоростью q₀, при которой свободная поверхность жидкости практически не деформируется (режим I, рис. 1), затем несущий газ подают с достаточно большой объемной скоростью q, при которой жидкость устойчиво разбрызгивается (режим Ш). В обоих случаях изменение температуры жидкости во времени фиксируется с помощью термометра Бекмана, а затем определяется скорость охлаждения жидкости – соответственно  и W_T.

В случае испарения воды с известной константой скорости в поток воздуха с относительной начальной влажностью e_н необходимость в измерении скорости охлаждения жидкости  без деформации поверхности отпадает, и возмущенную поверхность можно рассчитать по формуле (12) по результатам единичного опыта.

Физическая модель характеризуется тем, что основные процессы, протекающие в ней и в оригинале, имеют одинаковую физическую природу, хотя и нетождественны. Процесс в модели обычно схематизирован по сравнению с процессами в оригинале и может протекать в иных по абсолютной величине  пространственных и временных границах. При этом для изучения выделяют лишь наиболее существенные параметры процесса.

Рассмотрим в качестве физической модели системы (оригинала) жидкий чугун- струя кислорода низкотемпературную систему жидкость (например вода) – струя воздуха при комнатной температуре. Эта модель (рис. 3) позволяет определять скорость испарения жидкости по скорости ее охлаждения за счет эндотермичности процесса, а затем – площадь контакта фаз.

Скорость испарения воды в поток воздуха с относительной начальной влажностью e_н  определяется кинетическим уравнением:

                    (8)

Выразив скорость испарения жидкости W через скорость ее охлаждения W_т

,                              (9)

а изменение относительной влажности газа De в результате испарения жидкости через скорость испарения и объемную скорость потока газа

,        (10)

находим

           (11)

и окончательно расчетную формулу:

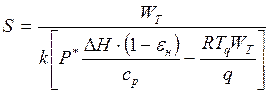               (12)

В уравнениях (8)...(12):  - скорость охлаждения жидкости, К/с; k – константа скорости, а  - теплота испарения жидкости; - теплоемкость системы при постоянном давлении;  - температура воздуха, К;  - давление насыщенных паров жидкости, Па.

В случае испарения дистиллированной воды можно принять следующие значения отдельных величин:

 , Па;  , моль/(Па×м²×с).

Относительную влажность воздуха определяют с помощью психрометра в соответствии с показаниями сухого и влажного термометра по прилагаемой таблице. Среднюю скорость охлаждения воды вычисляют по изменению температуры системы ΔТ за время продувки Δτ:

                                   (13)

Изменение температуры жидкости определяют известным графическим методом (рис. 4).

 

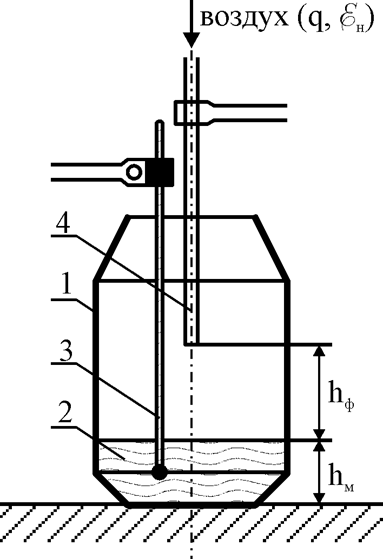Рис. 3. Физическая модель кислородного конвертера для изучения влияния интенсивности продувки (q) и высоты фурмы (h_ф) на площадь контакта жидкости со струей газа: 1- реактор (в масштабе 1:40); 2 – дистиллированная вода; 3 – термометр Бекмана; 4 – фурма.

 

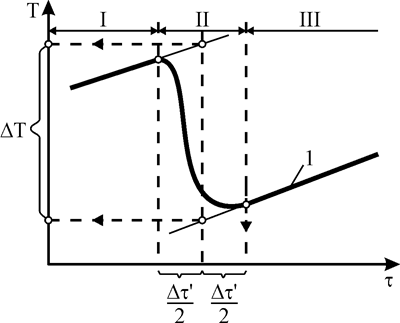Рис. 4. Графическое определение ΔТ. Периоды: –предварительный;  – главный; – заключительный. Как правило, продолжительность главного периода Δτ^´> Δτ.

Вариант 2.

В другом варианте методики в качестве физической модели выбирают низкотемпературную систему: раствор щелочи – струя газа, содержащего диоксид углерода СО₂. В этой системе происходит абсорбция диоксида углерода раствором щелочи. Процесс сопровождается экзотермическим эффектом и площадь контакта фаз при возмущении поверхности можно определить по скорости нагрева раствора :

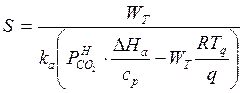,                             (14)

где и  - константа скорости и теплота абсорбции;  - парциальное давление СО₂ в исходной газовой смеси.