Определение площади поверхностей контакта фаз в системах металл-шлак-газ в условиях значительной их деформации методами физического моделирования: Лабораторный практикум, страница 2

В зависимости от степени деформации поверхности можно выделить три основных гидродинамических режима взаимодействия вертикальной струи газа с  одной или двумя несмешивающимися жидкостями: 1- без видимой деформации поверхности с возможным образованием «ряби» и волн; II – с образованием «лунки» конечных размеров с относительно «гладкой» поверхностью; III – с устойчивым разбрызгиванием жидкой фазы, взаимным эмульгированием в случае продувки двух несмешивающихся жидкостей, внедрением струи газа в жидкость и дроблением ее на пузырьки. В I режиме (0£q£q₁) площадь контакта фаз практически равна площади свободной поверхности , во II (q₁£q£q₂) – площадь контакта фаз монотонно возрастает с увеличением q по закону:

,                              (4)

а в III (q>q₂):

 

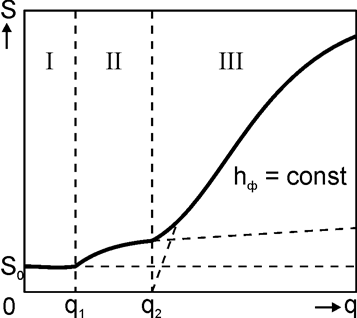Рис. 1. Зависимость площади контакта жидкости с газом или двух несмешивающихся жидкостей от объемной скорости струи газа.

 

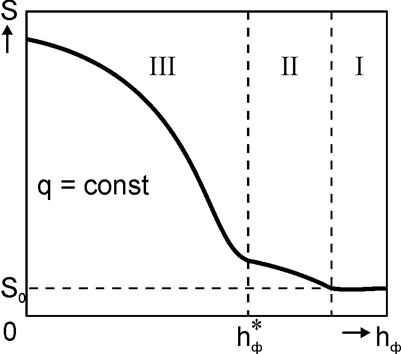Рис. 2. Изменение площади контакта двух фаз в зависимости от уровня фурмы над свободной поверхностью жидкости.

             (5)

В уравнениях (4) и (5): К₁, К₂ и К –коэффициенты пропорциональности, зависящие от физических свойств взаимодействующих фаз и геометрических параметров реактора и дутьевого устройства; q₁ – объемная скорость струи газа, при которой на поверхности жидкости появляется лунка конечных размеров (теоретически q₁ ® 0, а практически - это объемная скорость, ниже которой деформацией поверхности еще можно пренебречь); q₂ – объемная скорость газа, достаточная для устойчивого разбрызгивания продуваемой жидкости (металла); n – показатель степени, меняющийся в относительно узких пределах 0,4...0,7. Для данной системы жидкость (1) – жидкость (2) – газ и дутьевого устройства величина q₂ зависит только от высоты фурмы h_ф:

,                          (6)

где - коэффициент пропорциональности, зависящий от физических свойств жидкости и газа, от толщины слоя верхней жидкости (“шлака”) и геометрических характеристик дутьевого устройства (фурмы); m – показатель степени, близкий к 1.

Именно этой зависимостью обусловлено изменение площади контакта с изменением h_ф (см. рис. 2). На этом рисунке выделена предельная высота фурмы , которую можно назвать “дальнобойностью” струи. При h_ф>h_ф^* струя практически не разбрызгивает жидкость, а величина S®S₀.

С учетом уравнений (5) и (6) нетрудно показать, что дальнобойность струи газа для данной системы однозначно определяется объемной скоростью газа:

.

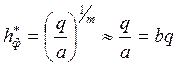Методика определения площади контакта жидкости и газа.

Вариант 1.

Если в качестве низкотемпературной  модели выбрать процесс испарения жидкости в потоке несущего газа, то по суммарной скорости испарения и его константе удается найти площадь деформированной поверхности. О скорости испарения жидкости при этом можно судить по убыли ее массы или объема за время продувки. Однако при заметном брызгоуносе последнее обусловливает низкую точность определений. А вот изменение температуры жидкости малочувствительно к брызгоуносу, практически целиком связано с испарением и легко учитываемым теплообменом с окружающей средой.

Поэтому, с целью повышения точности и расширения области применимости способа определения площади контакта жидкости со струей несущего газа, в процессе продувки измеряют температуру жидкости и определяют площадь контакта фаз по соотношению

,                        (7)

где S и S₀ – соответственно площадь деформированной и недеформированной струей газа поверхности жидкости, м²; W_T – скорость изменения температуры жидкости, К/с; q – объемная скорость несущего газа при продувке с деформацией поверхности, м³/с;  - скорость изменения температуры жидкости при продувке без деформации поверхности с объемной скоростью q₀, K/с; ; R –универсальная газовая постоянная, Дж/(моль×К); Т – температура несущего газа, К; С_р –теплоемкость системы, Дж/К; Р – давление насыщенного пара жидкости, Н/м²; DН – теплота испарения жидкости, Дж/моль.