Построение однофакторных регрессионных моделей для прогноза: Методические указания к выполнению практических занятий по дисциплине «Планирование на предприятии»

Предназначены для студентов специальности «Экономика и управление на предприятии (горной промышленности и геологоразведки)» (060800).

ВВЕДЕНИЕ

При статистическом исследовании корреляционных связей одной из основных задач является определение их формы, тоесть построение модели связи.

При построении регрессионной модели проводится несколько этапов: предварительный теоретический анализ, определение объекта, отбор факторов, сбор и подготовка информации, выбор модели связи, исчисление показателей тесноты корреляционной связи, оценка адекватности регрессионной модели.

1. Методические указания

1.1  Вычисление параметров корреляционных линейных уравненийпо первичным данным

Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой

,                                          (1)

где y – индивидуальные значения результативного признака;

x – индивидуальные значения факторного признака;

a₀ , a₁ – параметры уравнения прямой (уравнения регрессии);

y_x – теоретическое значение результативного признака.

Параметры уравнения прямой a₀ и a₁ определяются путем решения системы нормальных уравнений, полученных методом наименьших квадратов или по формулам

                                         (2)

   

                       (3)

                               (4)

Параметр уравнения регрессии в виде свободного члена возможно подсчитать по следующей формуле :

                                     (5)

Ясно, что практически приемлемым является наименее трудоемкий вариант расчета ( возможно производить расчеты на компьютере).

В уравнении прямой параметр a₀ экономического смысла не имеет. Параметр a₁ является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу. Часто исследуемые признаки имеют разные единицы измерения, поэтому для оценки влияния факторного признака на результативный применяется коэффициент эластичности. Он рассчитывается для каждой точки и в среднем по всей совокупности. Коэффициент эластичности (Э) определяется по формуле

                                               (6)

где  - первая производная уравнения регрессии.

Средний коэффициент эластичности определяется для уравнения прямой по формуле

                                                   (7)

Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.

1.2  Определение параметров линейного однофакторного уравнения регрессии по сгруппированным данным

Если данные сгруппированы и представлены в виде корреляционной таблицы, то параметры линейного уравнения регрессии могут быть определены путем решения следующей системы нормальных уравнений:

 

                                                                               

                                                   (8)

или по формулам

                             (9)

                                   (10)

где  - групповые средние.

Параметр a₀ уравнения регрессии можно определить также и по формуле (5).

1.3   Расчет параметров степенной функции

Если значения факторного признака расположены в порядке геометрической прогрессии и соответствующие значения результативного признака также образуют геометрическую прогрессию, то связь между признаками может быть представлена степенной функцией вида

                               (11)

Для определения параметров степенной функции методом наименьших квадратов необходимо привести ее к линейному виду путем логарифмирования:

lg y = lg a₀ + a₁lg x.                                 (12)

Система нормальных уравнений имеет вид

 

                                                          (13)

Параметры можно определить, решая систему нормальных уравнений или по формулам

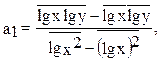                                           (14)

                                            (15)

или

                  (16)

                             (17)

Параметр a₁ логарифмической функции является коэффициентом эластичности, который показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.

1.4   Расчет параметров уравнения гиперболы

Если результативный признак с увеличением факторного признака возрастает (или убывает) не бесконечно, а стремится к конечному пределу, то для анализа такого признака применяется уравнение гиперболы вида

                                         (18)

Для определения параметров этого уравнения используется система нормальных уравнений

                                  (19)

Чтобы определить параметры уравнения гиперболы методом наименьших квадратов, необходимо привести его к линейному виду. Для этого произведем замену переменных , получим следующую систему нормальных уравнений:

 

                                       (20)

Параметры уравнения гиперболы можно вычислить по формулам

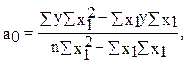                            (21)

                                (22)

1.5 Статистические методы измерения тесноты корреляционной связи между двумя признаками

Одним из важнейших этапов исследования корреляционной связи является измерение ее тесноты. Для этого применяются: линейный коэффициент корреляции, теоретическое корреляционное отношение, индекс корреляции.

Линейный коэффициент корреляции вычисляется по формулам и применяется