Комбинированная разработка месторождений: Методические указания по выполнению лабораторных работ, страница 5

                                                                                                            (1.11)

где 2h_обb /3 – площадь параболического сегмента

                                                                                                            (1.12)

Мощность оставщшейся потолочины

                                                                                                            (1.13)

При h_об>H  h_п имеет отрицательное значение, т.е. обрушение выйдет на поверхность на уровне отметки H (рис. 1.2) в форме параболического цилиндра, в основании которого лежит усеченный сегмент MKCD параболы площадью

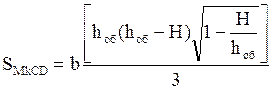                                                                                                            (1.14)

Установлено, что образующаяся при этом воронка имеет также вид параболы с основанием b^/, поперечное сечение воронки будет равно площади параболического сегмента /8/

S_в =2h_вb^//3,

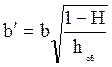, тогда

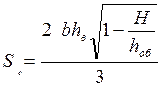,                                                                                                            (1.15)

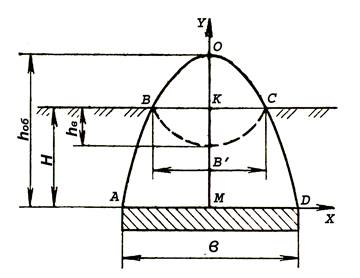
Рисунок 1.2  - Форма воронки обрушения

Причем, из условия компенсации обьемов пустот за счет коэффициента разрыхления имеем:

,

С учетом (1.14) , тогда

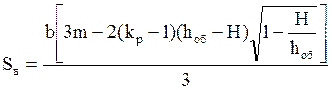                                                                                                            (1.16)

Приравняв выражения (1.15) и (1.16) с учетом (1.12), получим глубину воронки провала

h_в=1,5m-H(k_р-1)                                                                                                            (1.17)

При h_об = H выражение (1.17) не имеет смысла, так как воронка не образуется из-за того, что обрушение достигнет поверхности и его пространство будет заполнено горной массой выработанного пространства.

При отработке слепых залежей на обособленных участках, когда ширина и длина обрушения примерно равны (, для прогнозирования состояния поверхности с большим запасом прочности расчет параметров обрушения можно производить из условий обрушения налегающих пород по эллиптическому параболоиду, главными осями которого являются ширина b и длина L блока (выработанного пространства), а третьей полуосью – высота обрушения (рисунок 1.1в).

Объем сегмента параболоида равен произведению площади на половину высоты. В приведенном случае основанием тела обрушения считают прямоугольник, площадь которого можно принять для расчета с достаточной для горного дела точностью.

                                                                                                             (1.18)

Аналогично (1.5), (1.6), (1.7) найдем

                                                                                                            (1.19)

Мощность потолочины

,                                                                                                            (1.20)

При h <0 образуется воронка. Она имеет вид параболоида с основанием на высоте H, оси которого (хорды главных сечений параболоида обрушения) будут:

;                                 

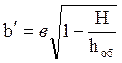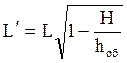
Тогда аналогично (1.18) объем воронки можно определить из выражения

,                                                                                                            (1.21)

Кроме того, обьем воронки обрушения можно определить из выражения

 

где V_об(H) – обьем обрушения усеченного на высоте H параболоида. Его определяют как разность обьемов полного параболоида обрушения и верхней части, отсеченной плоскостью поверхности на высоте h_об-H:

,

тогда

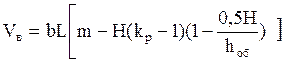,                                                                                                            (1.22)

Приравняв выражение (1.21) и (1.22) с учетом (1.19),получим

.                                                                                                            (1.23)