Программирование в MS Visual C++. Написание программы генератора случайных чисел от 0 до 100

объявляем первое число x1, которому присваиваем значение 9. А переменная x2 нужна для сохранения предыдущего значения x1. Данная строка: x1 = ((~x1<<2 ^ x2<<1 *i )*(~x1<<1 ^ x2<<2*i )+ (~x1<<4 ^ x2<<5*i)) % 101;

На самом деле проста.

~ - это инверсия.

<< - это сдвиг числа.

^ - это исключающее ИЛИ, а по простому она называется XOR.

% - это остаток от деления. То есть наши числа будут от 0 до 100.

Задача 2

Дан одномерный массив (вводиться с клавиатуры). Необходимо, заполнить одномерный массив, сделать вывод одномерного массива.

#include "stdafx.h"

#include <iostream>

#include <conio.h>

const int n = 5; //объявляем константу для массива

void main () {

int x[n]; //объявляем переменный дробного типа

int i; //переменная для цикла

int sred = 0; //Переменная целого типа для вычисления суммы

for (i = 0; i < 5 ; i++){

std::cout<<"x["<<i<<"] = "; //На экран выводится  ‘x[i] = ‘

std::cin>>x[i]; // вводим с клавиатуры целые числа

}

std::cout<<"\n"; //Переход на следующую строку

for (i = 0; i < 5 ; i++){

std::cout<<"x["<<i<<"] = "<<x[i]<<"\t";

//На экран выводится результат нашего ввода

}

for (i = 0; i < 5 ; i++){

sred = sred + x[i]; //суммируем элементы массива

}

std::cout<<"\n"; //Переход на следующую строку

sred = sred/n;

std::cout<<"Sred = "<<sred<<std::endl;

//На экран монитора выводится сообщение ‘x + y = 13’

_getch(); //Экран не закрывается, пока не зажата любая клавиша

}

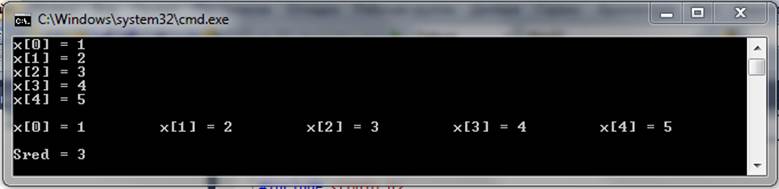
Рисунок 2 – Результат выполнения программы

Задача 3

Дан двухмерный массив (ввод с клавиатуры). Необходимо, сделать ввод/вывод двумерного массива. Найти максимальный элемент двумерного массива.

#include "stdafx.h"

#include <iostream>

#include <conio.h>

const int n = 3; //объявляем константу для массива

void main () {

int x[n][n]; //объявляем массив целого типа

int i,j; //переменная для цикла

int max = 0; //Переменная для вычисления максимального числа

for (i = 0; i < n ; i++)

for (j = 0; j < n ; j++){ //цикл ввода массива

std::cout<<"x["<<i<<","<<j<<"] = "; //На экран выводится ‘x[i][j] = ‘

std::cin>>x[i][j]; //вводим с клавиатуры целые числа

}

std::cout<<"\n"; //Переход на следующую строку

for (i = 0; i < n ; i++){ //цикл вывода массива

std::cout<<"\n"; //Переход на следующую строку

for (j = 0; j < n ; j++){

std::cout<<"x["<<i<<"]"<<"["<<j<<"] = "<<x[i][j]<<"\t"; //На экран выводится результат нашего ввода

}

}

max = x[0][0]; //Допустим максимальное число – это первое число массива

for (i = 1; i < n ; i++){ //цикл нахождения максимального элемента массива

std::cout<<"\n"; //Переход на следующую строку

for (j = 0; j < n ; j++){

if (x[i][j]> max) max = x[i][j]; //если есть число большее, чем max

//тогда max принимает значение этого числа

}

}

std::cout<<"\n"; //Переход на следующую строку

std::cout<<"Max = "<<max<<std::endl; //На экран монитора выводится максимальное число

_getch(); //Экран не закрывается, пока не зажата любая клавиша

}

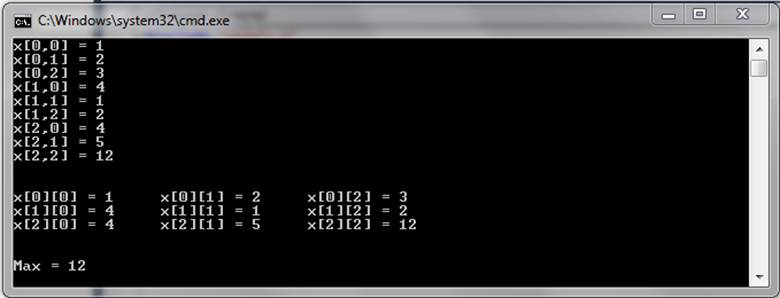
Рисунок 3 – Результат выполнения программы

Задача 4

4.1.  Метод Эйлера.

Решить дифференциальное уравнение уʹ=f(x,y) численным методом - это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n,

что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.             (1)

Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он  является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка  (1)

с начальным условием

x=x₀, y(x₀)=y₀              (2)

Требуется найти решение уравнения (1) на отрезке [а,b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность х₀, х₁, х₂,…, х_n, где x_i=x₀+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.

В методе Эйлера приближенные значения у(х_i)≈y_i вычисляются последовательно по формулам у_i+hf(x_i, y_i) (i=0,1,2…).

При этом искомая интегральная кривая у=у(х), проходящая через точку М₀(х₀, у₀), заменяется ломаной М₀М₁М₂… с вершинами М_i(x_i, y_i) (i=0,1,2,…); каждое звено М_iM_i+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку М_i. Если правая часть уравнения (1) в некотором прямоугольнике R{|x-x₀|≤a, |y-y₀|≤b}удовлетворяет    условиям:                                                                                                   

|f(x, y₁)- f(x, y₂)| ≤ N|y₁-y₂|  (N=const),                     (3)

|df/dx|=|df/dx+f(df/dy)| ≤ M  (M=const), то имеет место следующая оценка погрешности:

|y(x_n)-y_n| ≤ hM/2N[(1+hN)ⁿ-1],                                   (4)

где у(х_n)-значение точного решения уравнения (1) при х=х_n, а у_n- приближенное значение, полученное на n-ом шаге. 

Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом  h/2. Погрешность более точного значения уn* оценивается формулой

|y_n-y(x_n)|≈|y_n*-y_n|.                                       (5)

Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.

4.2.  Описание алгоритмов решения задачи

4.2.1.  Описание переменных

Таблица1 – Описание переменных.

4.2.2.  Блок- схема главного модуля

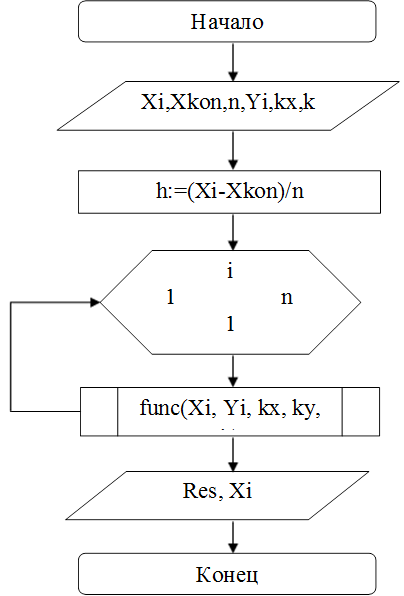4.2.3.  Описание алгоритма главной программы.

Таблица 2 - Описание алгоритма главной программы.

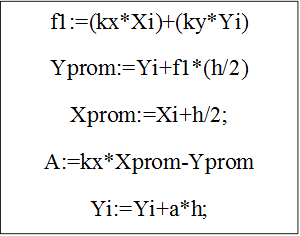
4.2.4.  Блок-схема функции “func”.

4.2.5.  Описание блок- схемы функции “func”.

Таблица 3 -Описание блок- схемы функции “func”.

4.3.  Программа решения дифференциального уравнения первого порядка методом Эйлера.

#include "stdafx.h"

#include <iostream>

#include <conio.h>

#include<iostream>

using namespace std;

void func(double& Xi, double& Yi, double kx, double ky, double h);

int main()

{

double h,Xi,Yi,Xkon,kx,ky;

int n;

cout<<"\t"<<"\t"<<"************************************************n";

cout<<"\t"<<"\t"<<"*                                                                *"<<"\n";

cout<<"\t"<<"\t"<<"*  Reshenie difurov  1  poryadka meodom  Eulera  *"<<"\n";

cout<<"\t"<<"\t"<<"*************************************************";

cout<<endl;

cout<<"Vvedite nachal'noe znachenie integrala [a,b,]=";

cin>>Xi;

cout<<"Vvedite konechnoe znachenie integrala [a,b]=";

cin>>Xkon;

cout<<"Vvedite chislo shagov=";

cin>>n;

h=(Xkon- Xi)/n;

cout<<endl;

cout<<"Vvedite nachal'noe uslovie y=";

cin>>Yi;

cout<<"Vvedite koefitcient pri x=";

cin>>kx;

cout<<"Vvedite koefitcient pri y=";

cin>>ky;

cout<<"|Interval|  Chislo  shagov |Shag prirasheniya|Nachal'noe  Y|Uravnenie   vida;|"<<"\n";

cout<<"|--------|-----------------|-----------------|-------------|-----------------|"<<"\n";

cout<<"|"<<"["<<Xi<<","<<Xkon<<"]"  <<"   |"<<n<<"                |"<<h<<"              |"<<Yi<<"            |"<<"y'="<<kx<<"x"<<"+"<<ky<<"y"<<"         |"<<"\n";

cout<<endl;

cout<<endl;

for (int i=1;i<=n;i++)

{

func(Xi,Yi,kx,ky,h);

cout<<"\n";

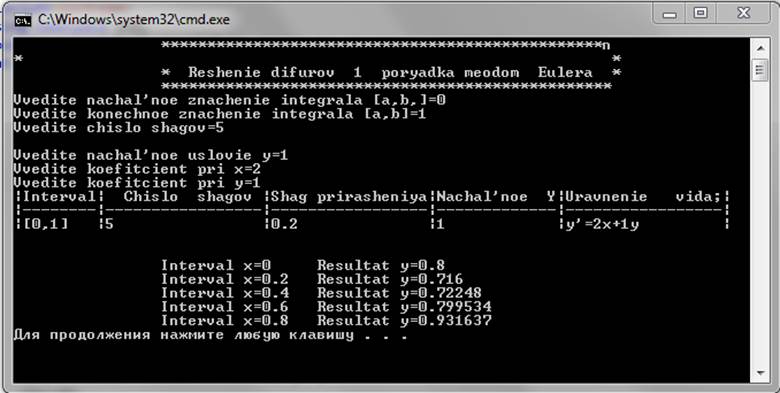
Рисунок 4 – Результат выполнения программы

Список использованных источников

1. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения), Н.С. Бахвалов. Главная редакция физико-математической литературы изд-ва «Наука», М., 1975г.

2. Методы, теории обыкновенных дифференциальных уравнений. Н.И. Гаврилов. Государственное издательство «Высшая школа» Масква-1962г