





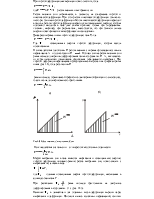

























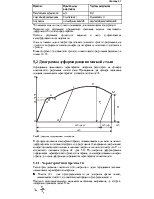

























Вблизи мест приложения нагрузок формулы сопротивления материалов несправедливы.
При использовании любых формул сопротивления материалов об этом принципе забывать нельзя и в местах приложения нагрузки предусматривать соответствующие места крепления, утолщения тела.
Глава 2. Геометрические характеристики поперечных сечений
Известны три геометрические характеристики, знакомые каждому — это длина, площадь, объем, которые имеют определенный физический смысл. В этой главе рассмотрим новые характеристики, которые будут использоваться в расчетных формулах сопротивления материалов: статические моменты и моменты инерции площади сечений. Эти характеристики не имеют физического смысла. Их нельзя измерить.
При выводе формул сопротивления материалов иногда случается, что часть формулы представляет собой интегральное выражение, зависящее только от формы и размеров сечения. Для упрощения последующего использования таких формул удобно такое выражение подсчитать заранее для различных форм сечений.
Статические моменты площади сечений используются при определении положения центра тяжести сечения, при расчете касательных напряжений при изгибе.
Моменты инерции используются при расчете напряжений и перемещений при изгибе и при кручении и т. д.
Статическими моментами площади сечений называются интегралы следующего вида
Sy = ∫ z d2 A
A
(2.1)
Sz = ∫ y2dA
A
У статических моментов нет физического смысла, но есть геометрическая интерпретация.
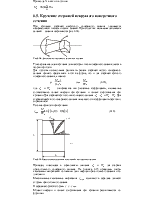
Рассмотрим сечение произвольной формы (рис. 2.1).
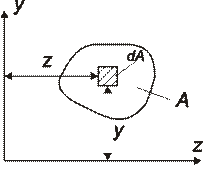
Рис.2.1. Геометрическая интерпретация статических моментов площади сечений
Выделим в сечении элементарную площадку dA с координатами y и z . Произведение площади dA на координату y есть элементарный статический момент dSz относительно оси z .Это понятие аналогично моменту силы относительно оси. Если предположить, что A — это вес пластины, имеющей форму нашего сечения, то статический момент Sz — это момент силы тяжести пластины относительно оси z .
Размерность статических моментов — ⎡длина3 ⎤ , обычно ⎡м3 ⎤ или ⎡см3 ⎤ .
⎣ ⎦ ⎣ ⎦ ⎣ ⎦
Статические моменты могут быть положительными, отрицательными или равными нулю.
Ось, относительно которой статический момент равен нулю, называется центральной.
Точка пересечения центральных осей называется центром тяжести сечения.
Статический момент составного сечения равен сумме статических моментов элементов этого сечения .
Это вытекает из свойств определенного интеграла, который можно вычислять по частям (в нашем случае по частям площади A ).
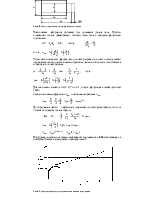
Рассмотрим изменение статического момента при параллельном переносе осей координат (рис. 2.2). Расстояние между старыми и новыми осями координат обозначим a и b . Пусть известны статические моменты относительно старых осей координат z – y . Найти статические моменты относительно параллельно перенесенных осей координат z1 – y1 .
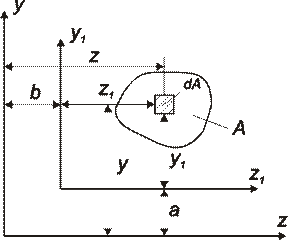
Рис.2.2. К определению статических моментов относительно параллельно перенесенных осей
По определению Sz1 = ∫ y1dA Sy1 = ∫ z d1 A .
A A
Выделим элементарную площадку dA и запишем связь между координатами площадки в старой и новой системах координат z1 = z − b y1 = y − a .
Тогда Sz1 = ∫ (y − a dA) = ∫ ydA − a dA∫ = Sz − aA
A A A
Аналогично Sy1 = ∫ (z − a dA) = ∫ zdA − b dA∫ = Sy − bA .
A A A
Найдем, на сколько надо сместить оси, чтобы они стали центральными.
![]() Sz
Sz
Sz1 = Sz − aA = 0 , a = yc = A ,
Sy
Sy1 =
Sy
− bA =
0
, b
=
zc
= ![]() A .
A .
Здесь yc и zc — координаты центра тяжести, но найти их пока нельзя, ведь Sz и Sy неизвестны.
Чтобы найти их, используем способ Мюнхгаузена, который сам себя за волосы из болота вытащил.
Если не известны координаты центра тяжести всего сечения, то разобьем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.