Основные теории катализа: мультиплетная, ансамблей, электронная, радикальная. Уравнение динамики нестационарных процессов, страница 3

Система послед.соед.РИП-выходы прод-тов приближ.к выходам прод-тов пр-са в 1-ом РИВ.

70. Кинетика реакций, проводимых в растворе.

При рассмотрении процессов в растворах необходимо учитывать структуру и природу растворителя и растворенного вещества, структуру, химический состав раствора и условия протекания реакции.

Растворители бывают полярные или неполярные Растворы: ионные и молекулярные, концентрированные и разбавленные, идеальные и неидеальные. Структура чистых жидкостей – пространственные группы молекул (тетраэдр, тригональная бипирамидальная, октаэдр и др). Из сочетания 2-х, 3-х и более полиэдров создается ансамбль полиэдров. Число молекул растворителя, окружают такую же молекулу или ион – координационное число. При растворении в растворителе жидкости, газа или тв. вещества происходит их диспергирование до молекул или ионного состояния. Молекулы или ионы растворенного вещества занимают пустоты в полиэдрах или разрушая их, создают новые.

Реагирующее вещество вступает не в форме индивидуальных молекул, а в форме сольватов. Молекула движется в «клетке» из молекул растворителя, движение колебательное и, следовательно, число столкновений больше, чем в газе, т. к. молекулы плотно упакованы в жидкости. W= kc_iⁿⁱ, k зависит от природы растворителя. Мономолекулярные реакции в жидкостях и в газовой фазе происходят с одинаковыми скоростями.

Пусть в растворе протекает реакция: A+B  A..B  C , раствор неидеальный.

По ЗДМ 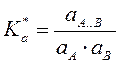 или 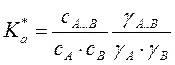,где a и y – активности и коэффициенты активности

Концентрация переходного состояния: . По теории переходного состояния , h-постоянная Планка При  получим  Скорость химической реакции зависит от природы растворителя. Так при y=10 скорость реакции в растворе в 10 раз выше чем в газовой фазе.При y=1 скорость реакции в растворе = скорости в газовой фазе.

Для мономолек.р-ции A ó A* -> продукты 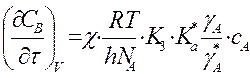  и при  получим:

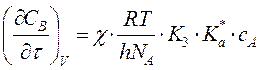, т.е. скорость реакции не зависит от природы растворителя.

71.

Влияние ионной силы на скорость реакции, проводимой в растворе.

Во всех уравнениях химической кинетики фигурируют концентрации реагирующих веществ. В термодинамике же константа равновесия неидеальной системы выражается через активности. Это обстоятельство необходимо учитывать, если в кинетическое уравнение входит константа равновесия. Правда, при реакциях в газовой фазе и между нейтральными молекулами в растворе в этом нет практической необходимости, но при рассмотрении реакций между заряженными частицами подобное пренебрежение может явиться источником существенных ошибок.

Для константы скорости бимолекулярной реакции A+ В → AВ* → продукты протекающей в растворе, теория активного комплекса, _;дает

κ=χ

Термодинамическая  константа  равновесия  между исхешшми веществами и активным комплексом κ^*= =

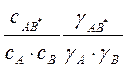
Комбинируя уравнения, получим уравнение Бренстеда — Бьеррума: κ=χ=К₀  для константы скорости реакции, протекающей в любой неидеальной среде. Величина К₀ имеет смысл константы скорости при бесконечном разведении, т. е. при γ= 1.

Если в качестве стандартного состояния выбрать бесконечное разведение, теория электролитов дает следующее приближенное соотношение для коэффициента активности: γ= ,где А — постоянная≈ 0,51; z —заряд иона; I— ионная сила раствора; β — некоторая постоянная, примерно обратно пропорциональная радиусу иона.

Если z_A и z_B  — соответствующие заряды реагирующих частиц, то реакция может быть записана в виде A^Za+B^zb→AB*(^Za+Zb) → продукты а подстановка  соответствующих  значений коэффициентов, активности в уравнение Бренстеда — Бьеррума дает

Рассмотрим два случая.

1. Взаимодействие между заряженными частицами.

Сумма  мала, и для случая взаимодействия между двумя ионами ими можно пренебречь, т. е.

Следовательно, логарифм константы скорости, согласно теории должен быть линейной функцией корня квадратного из ионной силы, а тангенс угла наклона прямой определяется соотношением зарядов реагирующих частиц.