Носитель- в-ва с высокоразв.пов-стью (уголь,силикагель,пемза,стекло) Он может в небол.пределах.изм.акт-ть кат-ра,проявляя опред.промотир.эф-кт. Устойч.адс.кат.к темп.и отравл.ядами повышается чем у мет.кат. Чтобы актив.кат-р его прогревают,но это мож.привести к спеканию. Носитель препятсв.спеканию,благодаря этому можно повыш.темп-ру проведения пр-са. Актив.компл.на кат.адсорбируются, но активна не вся пов-сть а только отд.участки-активн.центры. Число акт.ц. влияет на ск-сть пр-са.
Носитель для каталитически активных фаз выполняют роль матрицы,на к-ой формируется активная фаза.они могут участвовать в создании новых фаз,регулировать строение,состав полиэдров и число окисления катиона в составе полиэдра.
Актив.центры-атомы,спосбн.образовыватьпромежут.соед. (активир.комплексы)
Активный центр - особая часть молекулы фермента, определяющая её специфичность и каталитическую активность.
Активный центр непосредственно осуществляет взаимодействие с молекулой субстрата или с теми её частями, которые непосредственно участвуют в реакции.
67.Уравнение динамики нестационарных процессов.
Уравн.динамики-2
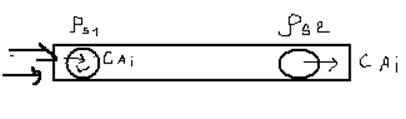
переменных-время и координата. Рассмотрим поток хим.реаг.в-в, проход.через сеч.L1 и L2,
наход.на расст.ΔL. В потоке хим. р-ция: 
Темп.в
реак-ре постоянна. Площадь сечения потока ρ. Лин.ск-сть потока в люб.сеч. u, а
конц.в-ва Ai в люб.сеч.C(Ai). Эти
величины переменные. Y(Ai) –кол-во в-ва Ai, реаг.к моменту
времени t в любом задан.объеме V/ Тогда
общ.уравнение димнамики проц.в потоке в режиме ид.выт.:
Пользуясь векторн.обознач.запишем:
68.Уравнение кинетики односторонней р-ции, проводимой в реакторе идеального вытеснения.
Ид.вытес.в
потоке - когда фронт газ. смеси в трубке имеет плоский профиль и отсутств. продольн.и
попереч. перемеш. смеси диффузией. В реакц.трубку сечением ρ(s1)
(1см2) поступает поток в-в с конц.в-ва Ai- c(Ai) и
проходит с лин.ск-тью V(м/с). За время dτ через сеч.ρ(s1)
(1см2) пройдет в-во А в кол-ве с(Ai)V dτ. Т.к. нестац.усл(кол-во в-ва на входе в р-р меняется
во врем.), кол-во в-ва Ai,проход.через сеч.l на расст. l+dl
запишем так: 
где 2ой член-накопл.в-ва в
заданном объеме. Определим это накопление:
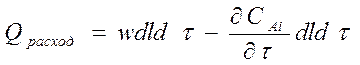
Qнакопл.=Qрасход
(расписать). Получаем: 
. При пост.ск-ти
подачи сырья (стац.усл) прав.часть=0.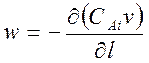 
.
V=V(a)/ρ(s), c(Ai)=n(Ai)/V(a). V(a)-об.ск-сть перемещ.реакц.смеси,м3/с. n(Ai)-кол-во
исх. Ai, кот.проходит ч/з сеч.р-ра на расст.l от
начала реакц.зоны, моль/с. Подставив, получим:
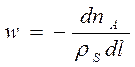. Если
n(A)=n(A0)(1-x), где n(A0)-мольн.ск-сть подачи в-ва Ai в р-р,
моль/с: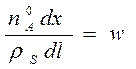 
69.Кинетика гомогенных реакций, проводимых в условиях идеального перемешивания.
Если в реактор, объем (V)
кот. может изменяться, вводят смесь реаг.в-в с объемн. скоростью V1
и отбирают с объемн.скор. V2, то кол-во молей любого в-ва в реак-ре будет изм-ся
во времени. Конц.в-ва Ai на входе = Coai. При ид.перемеш.
конц.в-ва на выходе из реакт. такая же как и в любой точке внутри него (Сai). w-истин.ск-сть хим.р-ции по в-ву Ai. Ур-ние мат.баланса: 
Реактор пост.объема,
жидк.в-ва. Имели объем V0
вначале,затем будет расти до объема реакт. 
. Подставляя получим
- ск-сть хим.р-ции при увелич. объема реаг.смеси. w=k*f*(CA1…CAk),эксперим.рассчит.конст. ск-стей хим.р-ций.
Если в РИП р-ция в газ.фазе: 
Откуда 
- ск-сть р-ции при изм.давл. в
реак-ре (давл.газов растет и раст.число молей Ai).Для ид.газов:
p-общ.давл.в р-ре в данный момент врем. ∑n-общ.число
молей в р-ре в данный момент времени.
Стацион.сост.в р-ре в
жид.фазе при пренебреж.изм.плотности в-в V1=V2=V
=> dV/dt=0. => V=const. V0=Vp=> число молей в р-ре не зависит от времени => dCAi/dt=0. 
Для газ.фазы 
причем V2 не
произвольна, иначе давл.в р-ре будет имз.со врем.и пр-с не будет стацион.
На выходе: 
на входе: 
Для жид.фазы(V1=V2): 
Для обратим.р-ций: 
Для необр. 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.