Диаграмма плавкости 2-х компонентных систем. Диаграммы плавкости систем с конгруэнтно и инконгруэнтно плавящимися соединениями, страница 5

- стандарт. сост-е для a₂ выбирается так, чтобы const=1, получаем:

- опытным путем получают a₂ и определяют  a_±  по ур-ю;

- вводят сред. ион. коэф. активности g_± и  срен. ион. моляльность m_±:

;                                 

 - можно выразить практич.коэф.актив.

·  Определение активности летучего вещества по парциальному давлению его пара.

Из уравнений: р₁=р*₁а₁, р₂=р*₂а₂, (где р₁ – парциальное давление пара растворителя над раствором, р*₁ – давление пара над жидким растворителем; р₂, р*₂ – соответственно для растворенного вещества) получаем

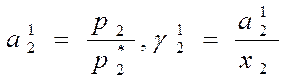
(индекс 1 указывает номер выбранного стандартного состояния)

Для определения γ твердого растворенного вещества выбираем второе стандартное состояние

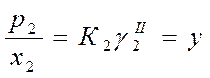
(у – вспомогательная расчетная величина, К₂ – константа Генри)

Получаем:

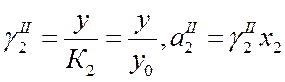
(где у=у₀ при х₂→0 находят графическим способом).

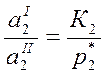
·  Определение активности растворенного вещества по давлению пара растворителя.

Из уравнения Гиббса-Дюгема: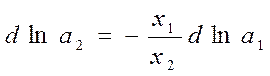       

Интегрирование дает: 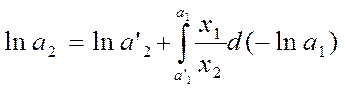            , где а’₁ и  a’₂ – активности растворителя и растворенного вещества при составе раствора х'₂, они должны быть известны.

Также можно проинтегрировать уравнение Гиббса-Дюгема, выраженное через γ:

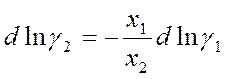
Активность а₁ определяют по давлению пара над растворами разного состава. Интеграл вычисляют графически.

·  Определение активности растворенного вещества по коэфф. распределения.

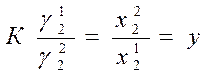
(где К – коэф. распределения, γ¹₂, γ²₂  - коэффициенты активности растворенного вещества в первом и втором растворителях, х¹₁, х²₂  - концентрации растворенного вещества в первом и втором растворителях).

а и γ можно вычислять также по понижению температуры замерзания, по повышению температуры кипения, по осмотическому давлению и по др. свойствам растворов.

29. Кондуктометрическое измерение константы диссоциации, степени диссоциации, точки эквивалентности при титровании.

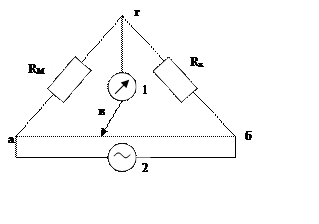Кондуктометрия – измерение электрической проводимости электролитов. Для измерения сопротивления электролитов применяется мостовая схема Уитстона:

2 – генератор переменного тока (постоянный вызывает   электролиз р-ра)

R_x – измерительная ячейка;

R_M – магазин сопротивлений (известно)

в – положение передвижного контакта (подбирается так, чтобы нуль-инструмент 1 не показывал ток или показывал min, тогда

R_x = R_M (R₁/R₂) = R_M (ав/вб)

Действительная электрическая проводимость р-ра определяется концентрацией раствора, природой компонентов и температурой. Истинная электрическая проводимость р-ра c пропорциональна экспериментально измеренной величине c’:         c=kc’,   где k – константа сосуда – хар-ка ячейки – зависит от площади электродов, расстояния м/у ними, формы сосуда, объема р-ра, проводящего ток, находят экспериментально c станд-ых р-ров, чаще всего КCl.

По экспериментальным данным рассчитываются значения удельной: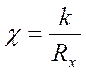           

и эквивалентной электропроводности:        

Для расчета степени диссоциации слабого электролита используется уравнение:

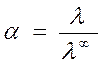,        где     λ^∞=l^¥_к+l_А^¥         - определяется по подвижностям ионов

Константу диссоциации бинарного электролита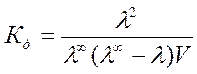 

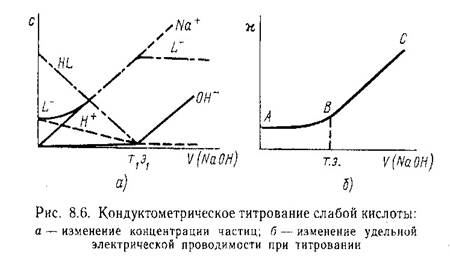
При кондуктометрическом титровании строится кривая зависимости электропроводности титруемого раствора от количества прибавленного титр. агента. Точка эквивалентности определяется по излому кривой этой зависимости. Резкое изменение электрической проводимости происходит, когда в процессе титрования образуются (или исчезают) малодиссоциирующие или труднорастворимые соединения.

Кислотно-основное титрование:

Изменение электрической проводимости до точки эквивалентности будут определяться действием 2-х взаимно противоположных тенденций: ¯ за счет ¯ с_Н+, имеющего подвижность 350 См×см²/(моль-экв), что намного превышает подвижность иона Na⁺

[50 См×см²/ (моль×экв)]

После точки эквивалентности начинается резкий электрической проводимости (ветвь ВС), т.к. в растворе будет нарастать концентрация ионов Na⁺  и ОН^-, подвижность кот. составляет 199 См×см²/ (моль×экв)