Определение минимальной частоты свободных колебаний системы при загружении рамы точечными массами

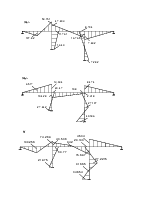
Дано: m₁=2 кг

M₂=4 кг

EI*10² кН*м=1

Q/ω_min=0.7

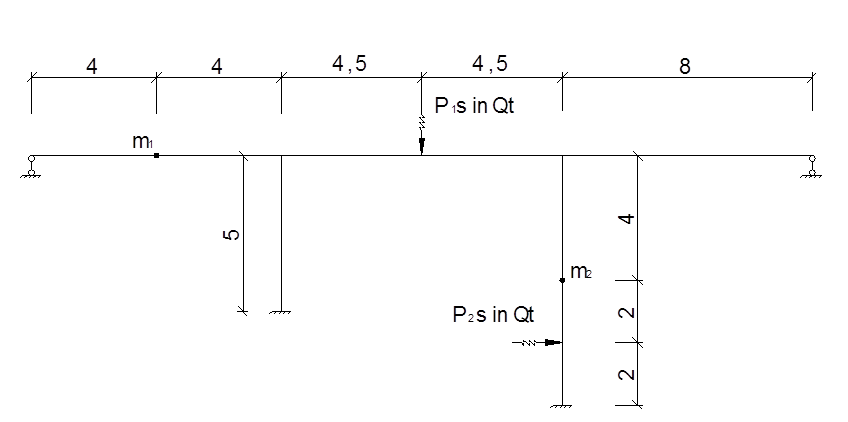
1.  Определение минимальной частоты свободных колебаний системы при загружении рамы точечными массами m₁ и m₂.

Частотное уравнение:

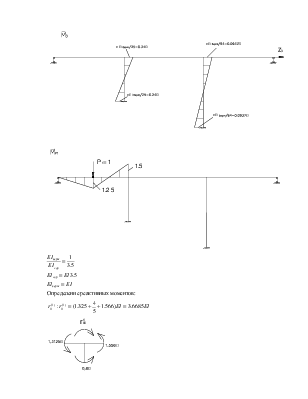
- перемещение в заданной системе от единичного загружения силами Р_n=1 в точке, где расположены массы m_n в направлении возможных колебаний.

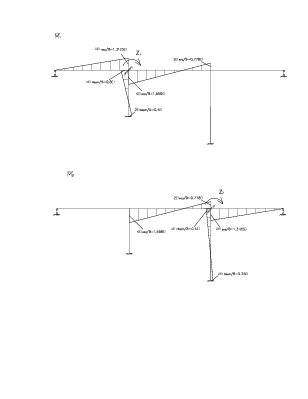
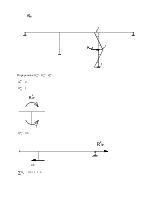
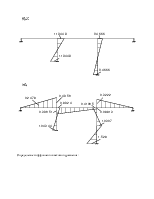
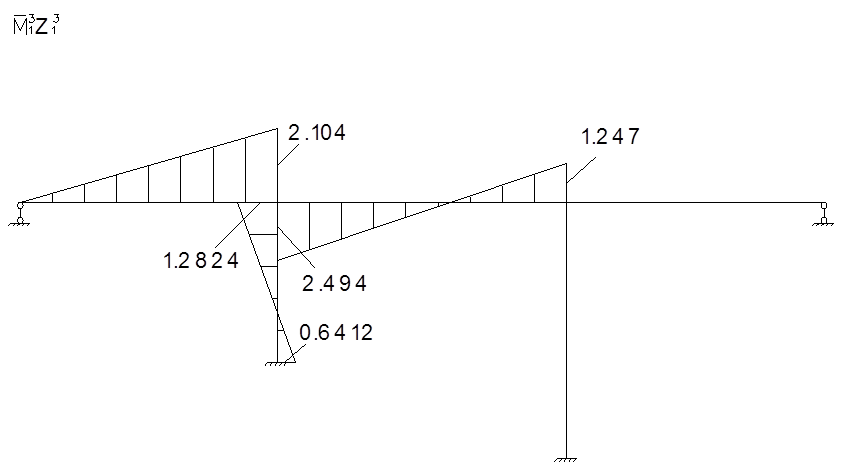
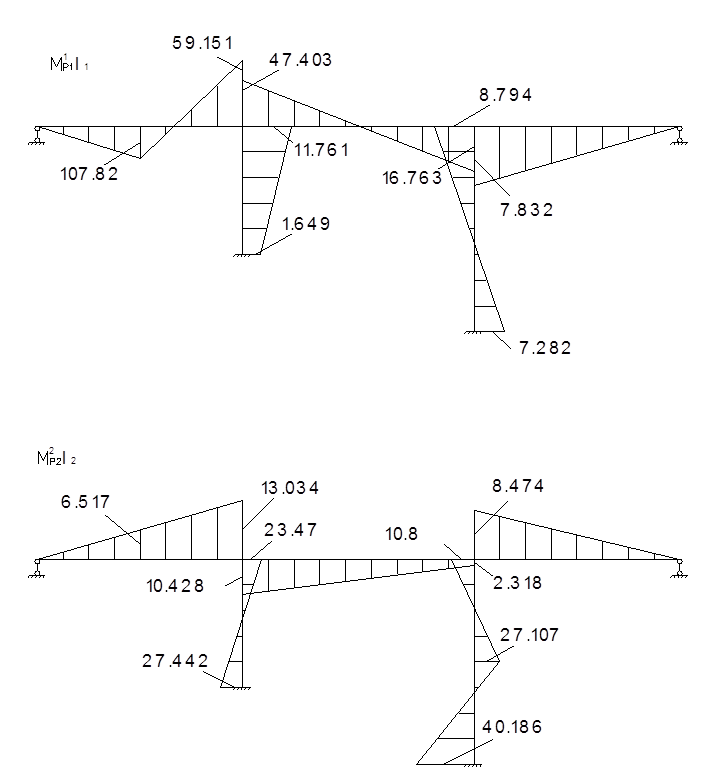
Для определения коэффициентов векового уравнения построим эпюру моментов в заданной системе от силы Р=1, в точке приложения массы m₁ в направлении возможных колебаний.

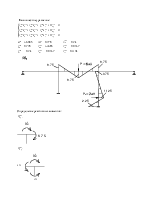
В развёрнутом виде канонические уравнения имеют вид:

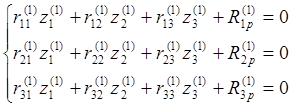
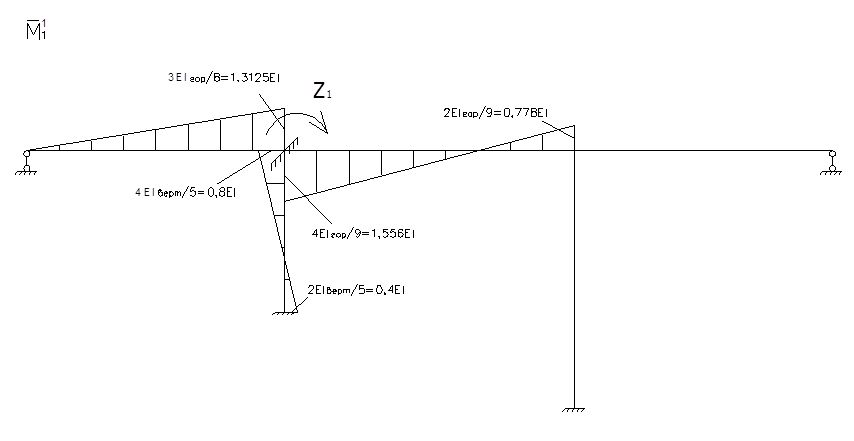
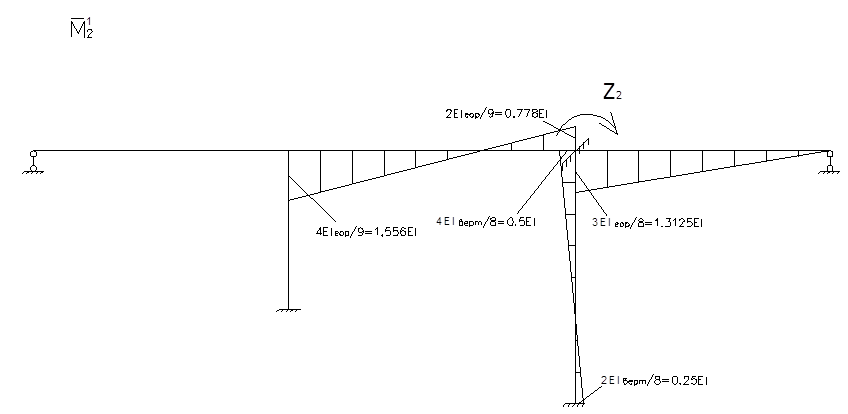
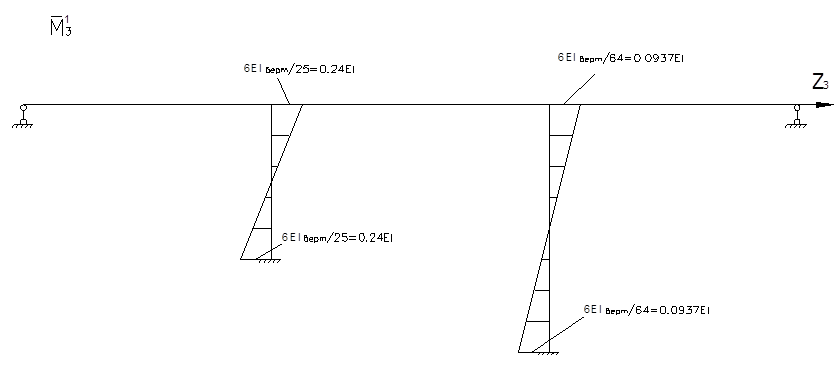
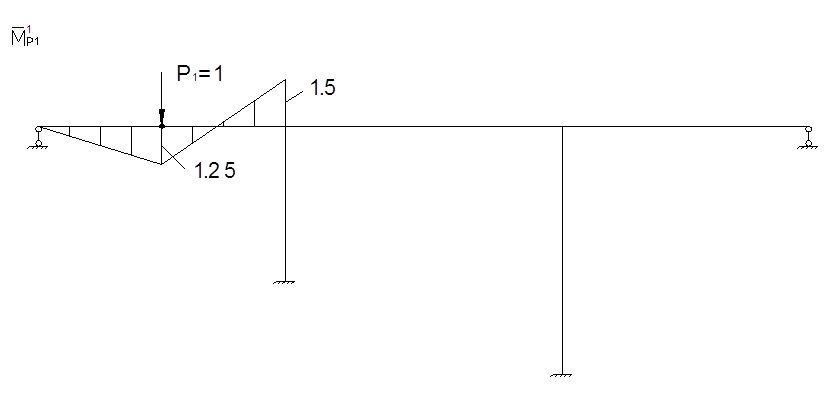
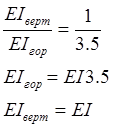
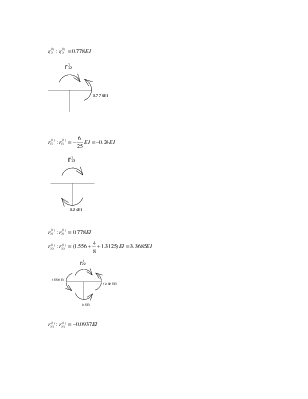
Определение реактивных моментов:

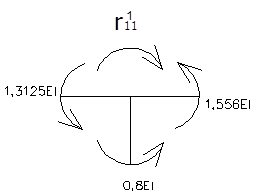
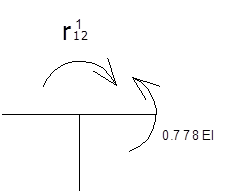
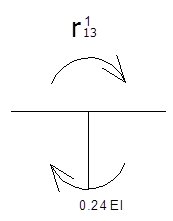
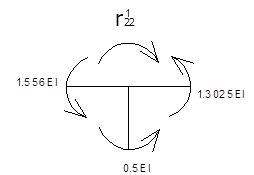
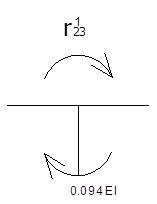
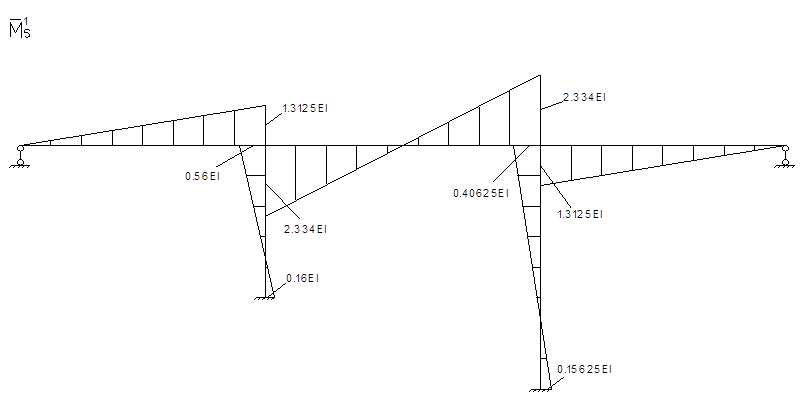
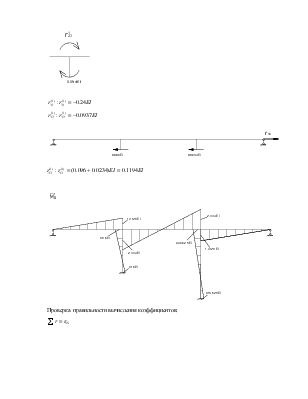
Проверка  правильности вычисления коэффициентов:

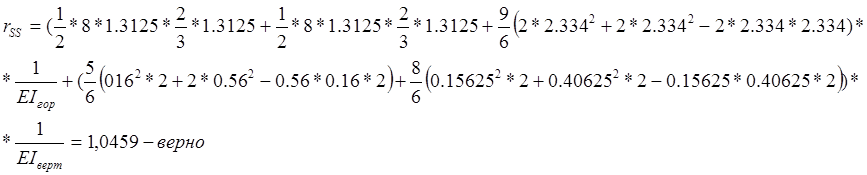
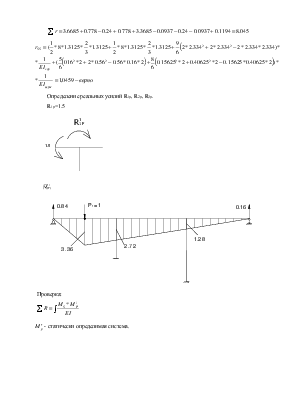
Определение реальных усилий R_1р, R_2р, R_3р.

R_1р=1.5

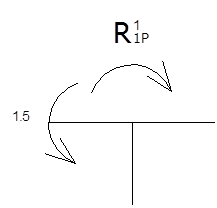
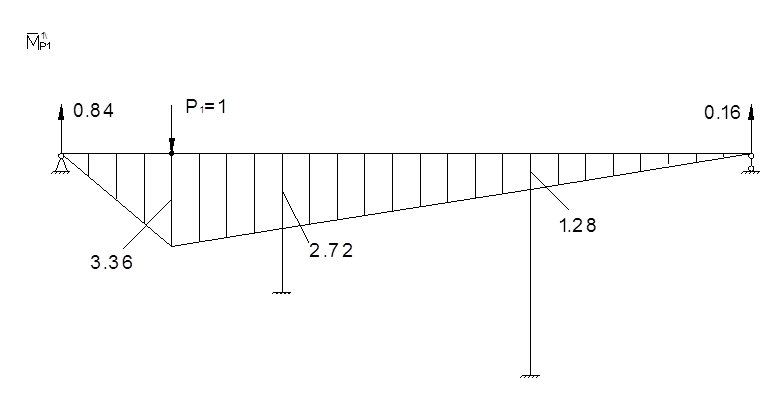
Проверка:

- статически определимая система.

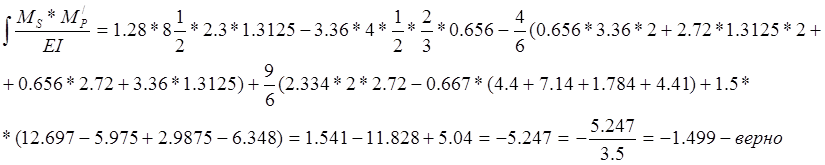
Решаем уравнение:

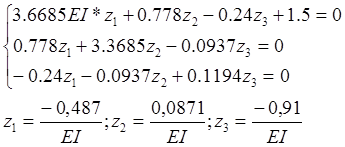
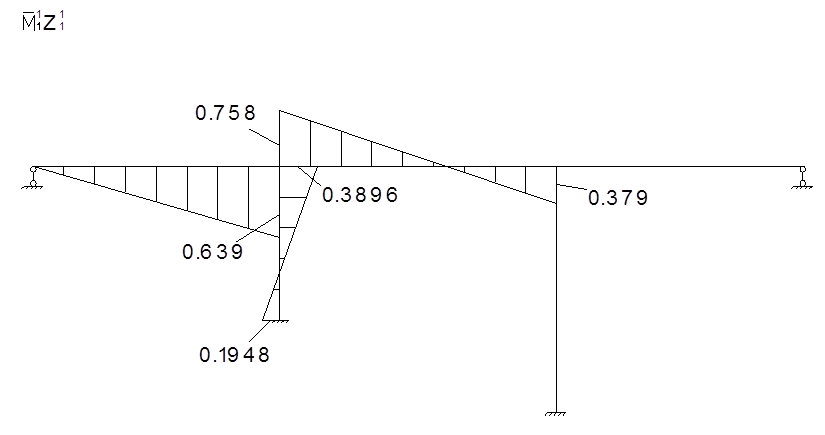
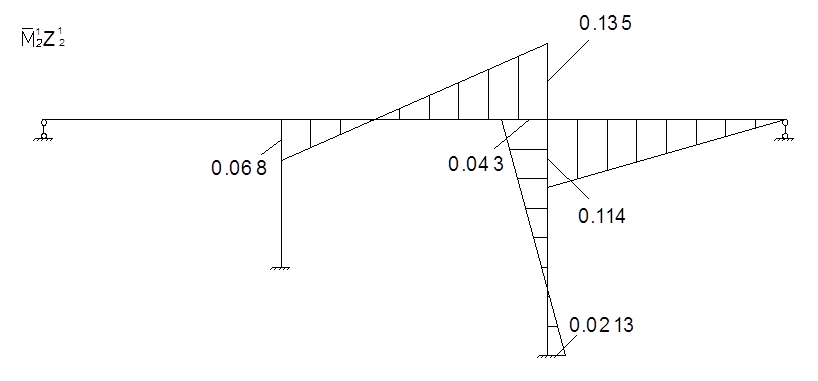
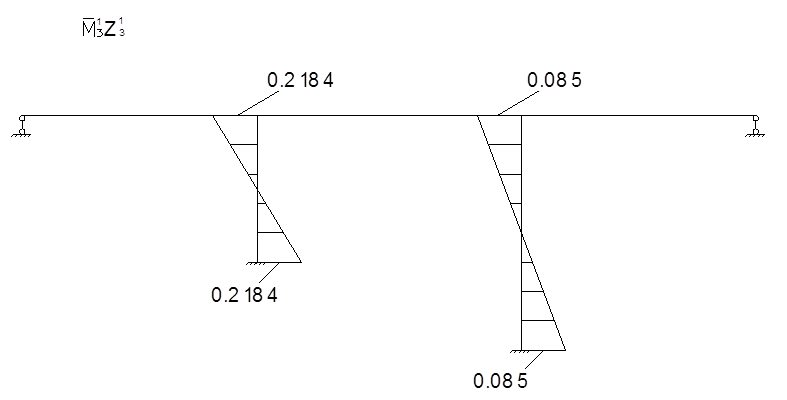
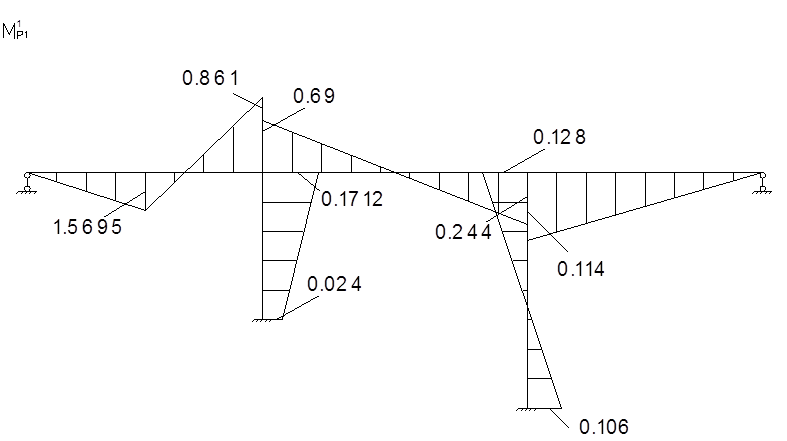
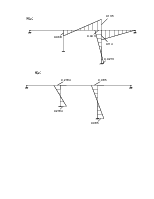
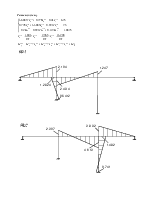
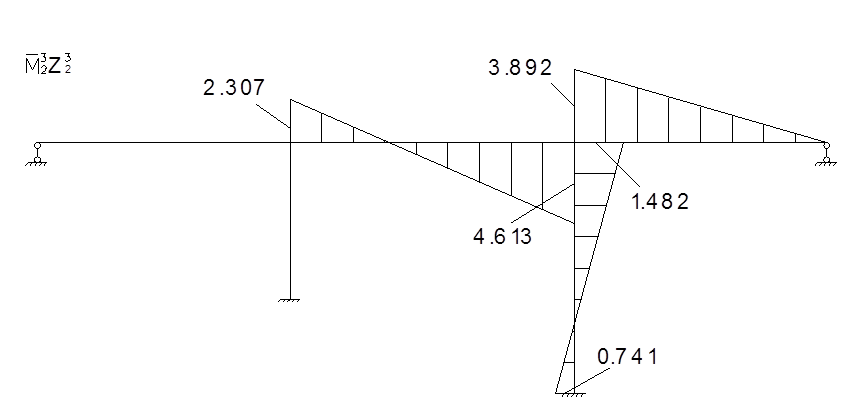
Для определения коэффициентов векового уравнения построим эпюру моментов в заданной системе от силы Р=1, в точке приложения массы m₂ в направлении возможных колебаний.

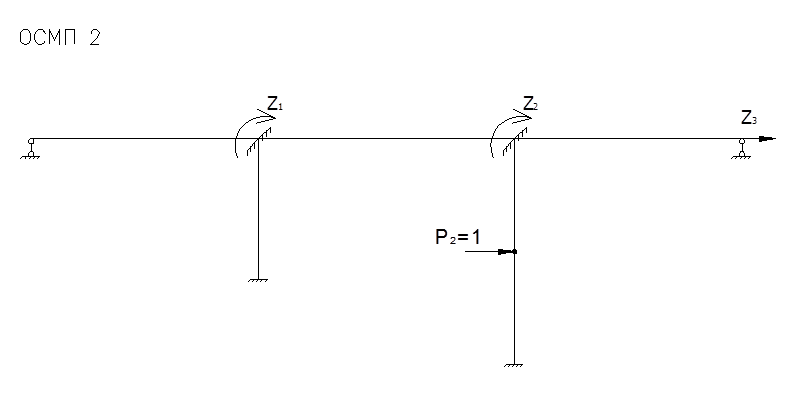
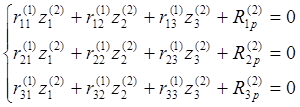
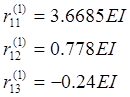
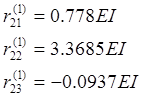
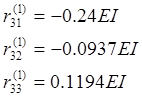
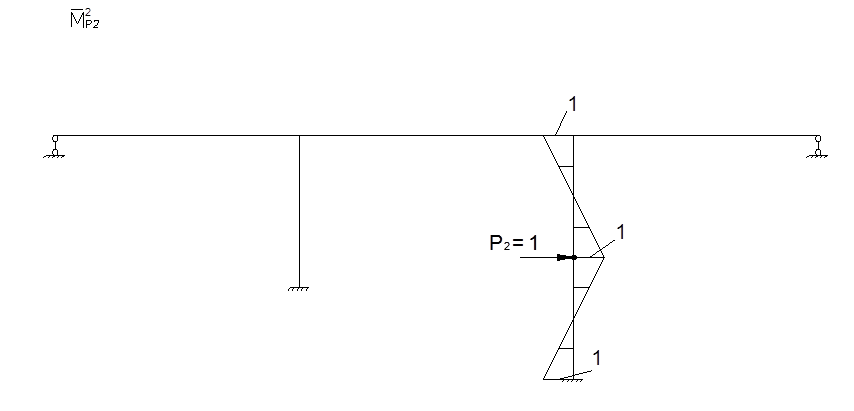
Определение , , .

,

,

.

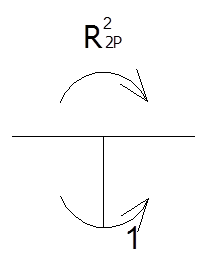
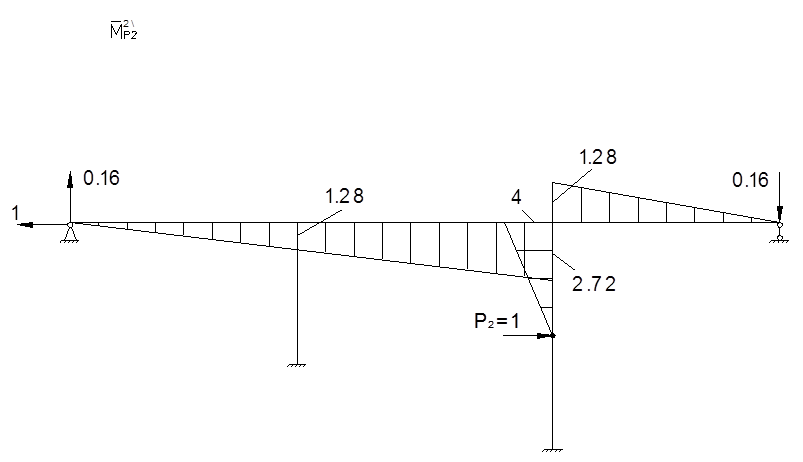
Проверка:

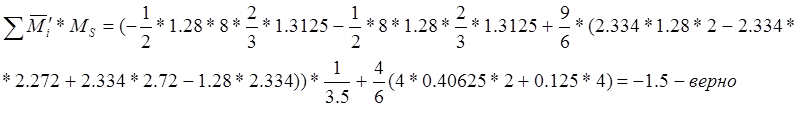
Решаем уравнение:

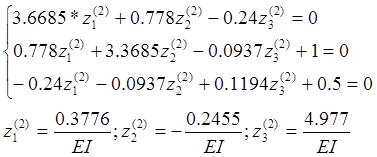
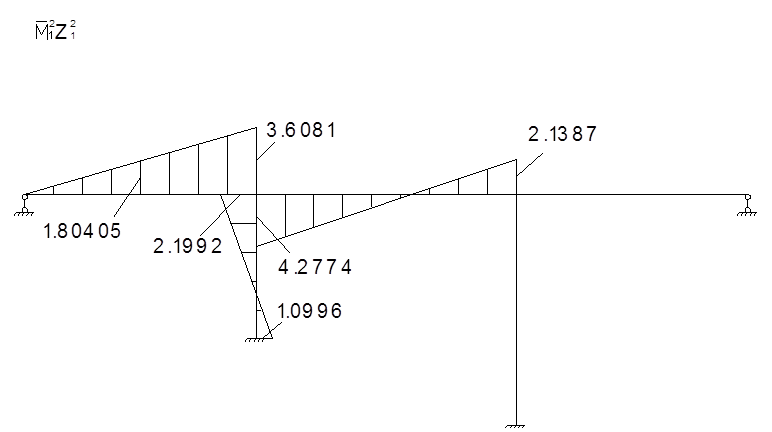
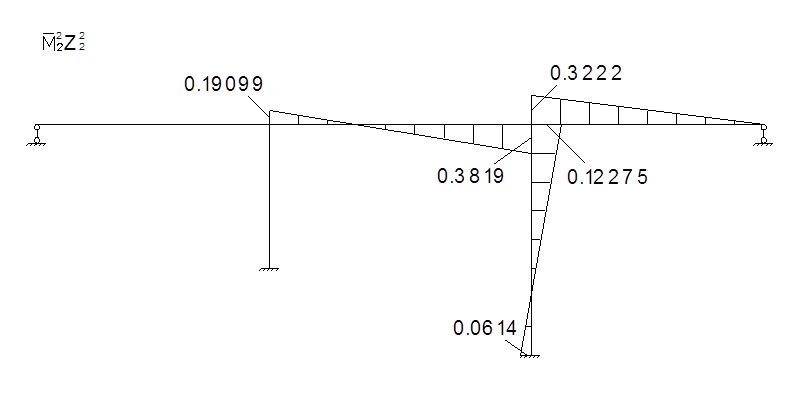
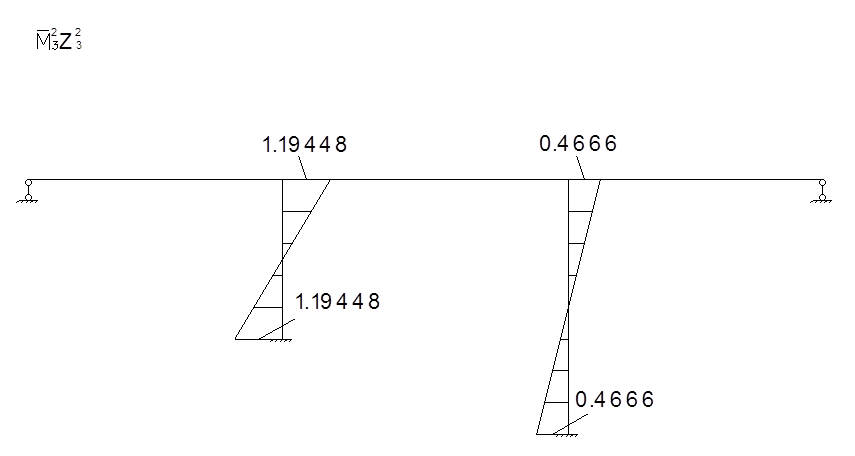
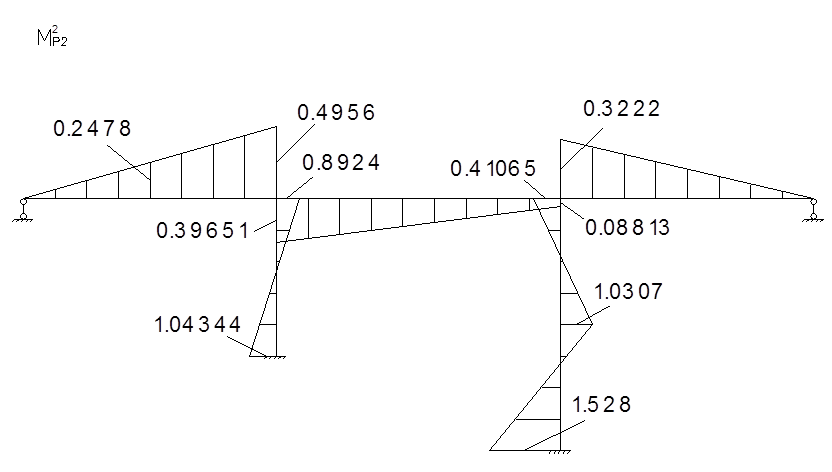
Определение коэффициентов векового уравнения:

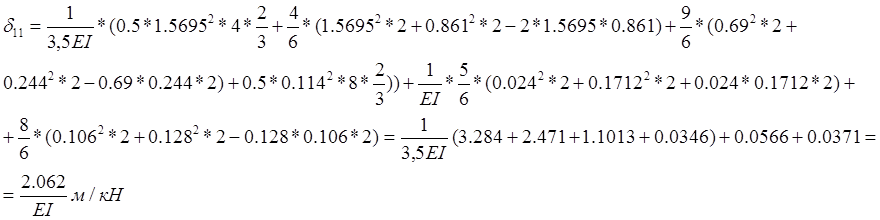
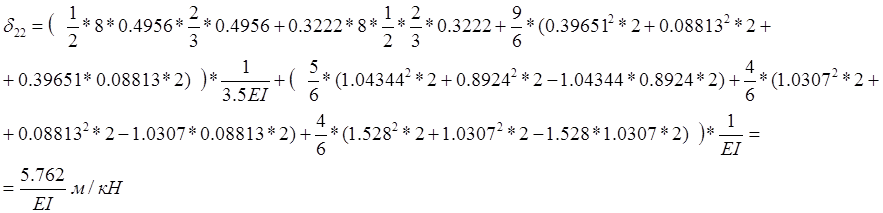
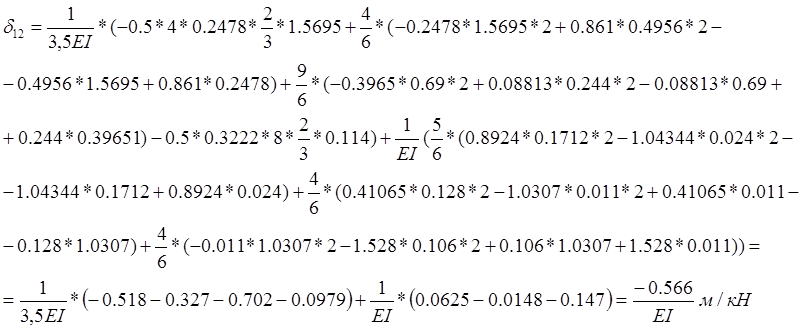
Решаем вековое уравнение:

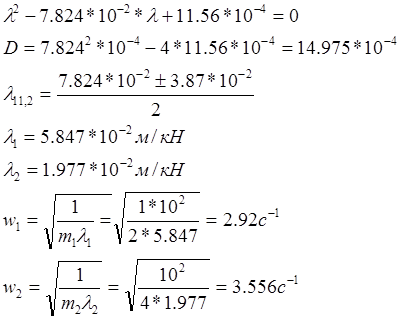
Выбираем w_min=2,92с^-1.

Определяем частоту вынужденных колебаний системы:

Определение значений изгибающих моментов от амплитудного воздействия вибрационных сил. Для этого составляем уравнение для определения сил инерции:

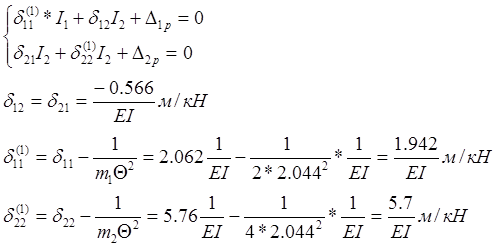
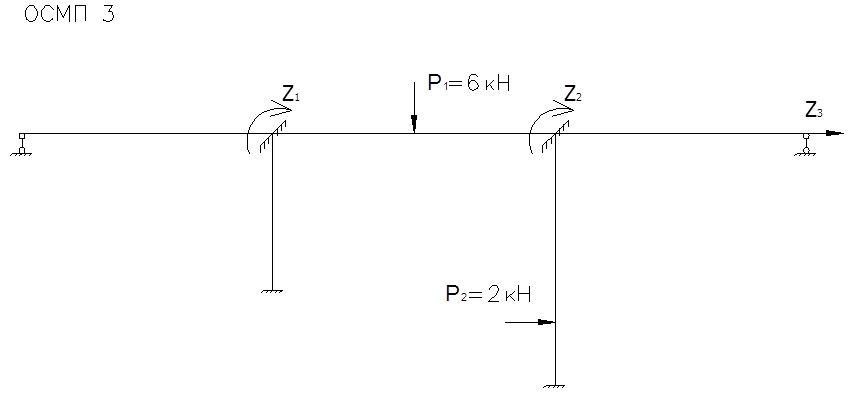
Каноническое уравнение:

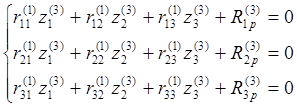
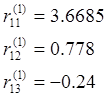
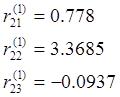
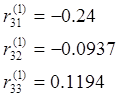
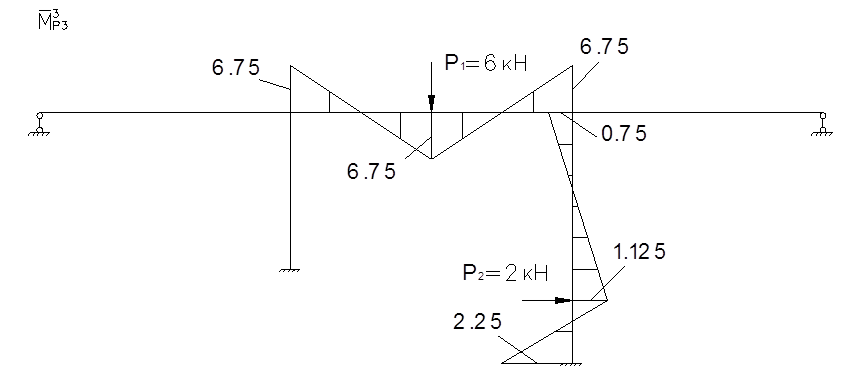
Определение реактивных моментов:

,

,

;

;

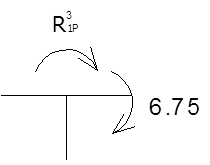
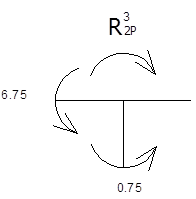
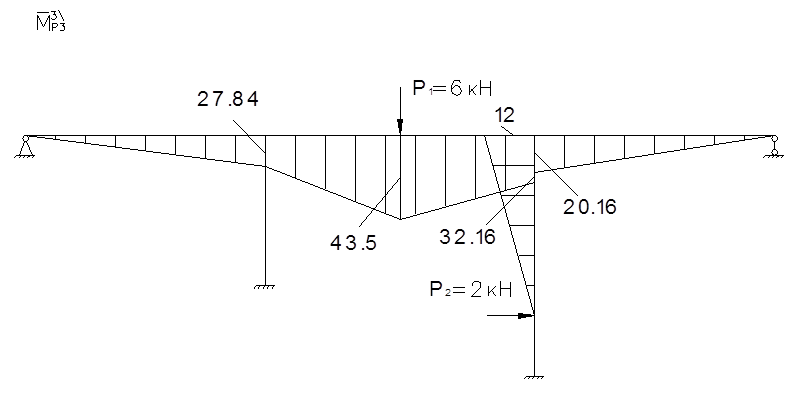
Проверка:

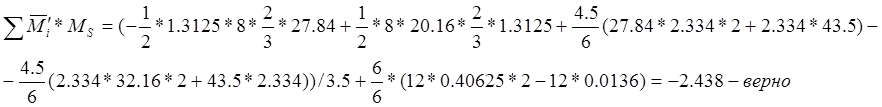
Решаем систему

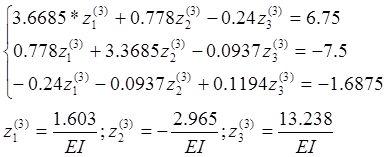
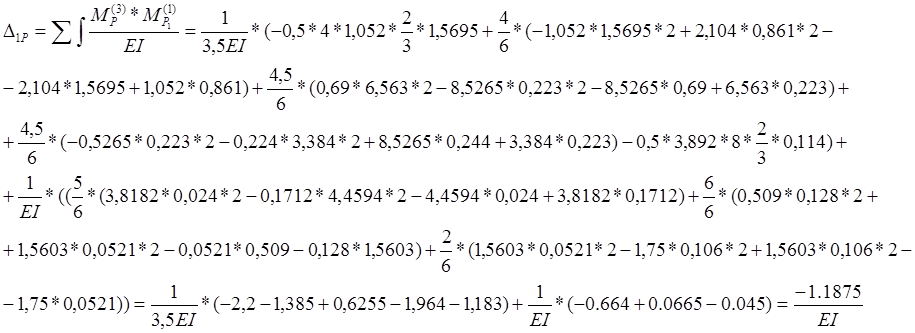
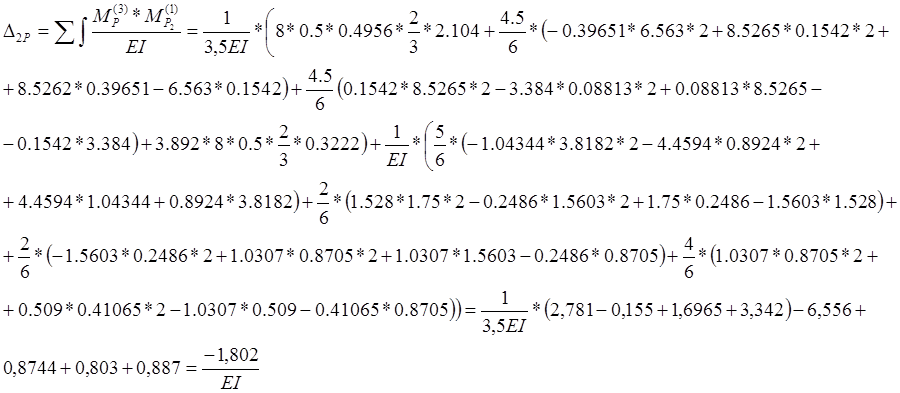Находим из системы уравнений I₁ и I₂ (инерционные силы).

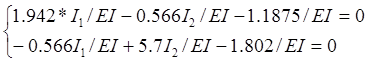
I₁ =  0,687*10²=68,7 кН*м

I₂ = 0,263*10²=26,3 кН*м

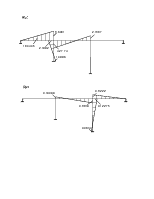
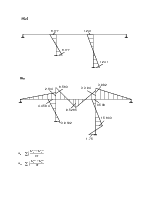
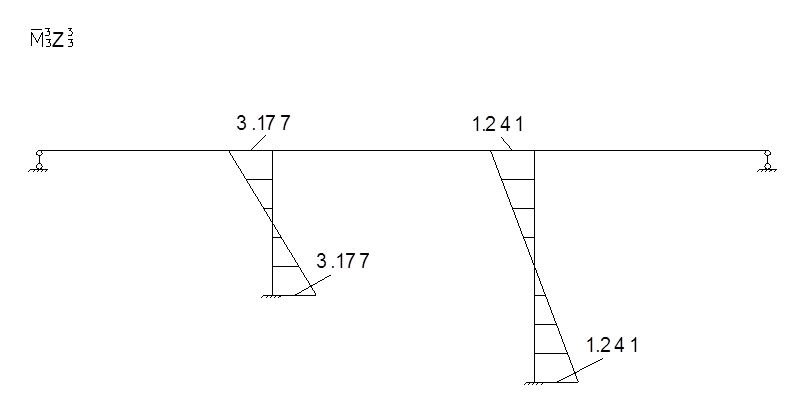
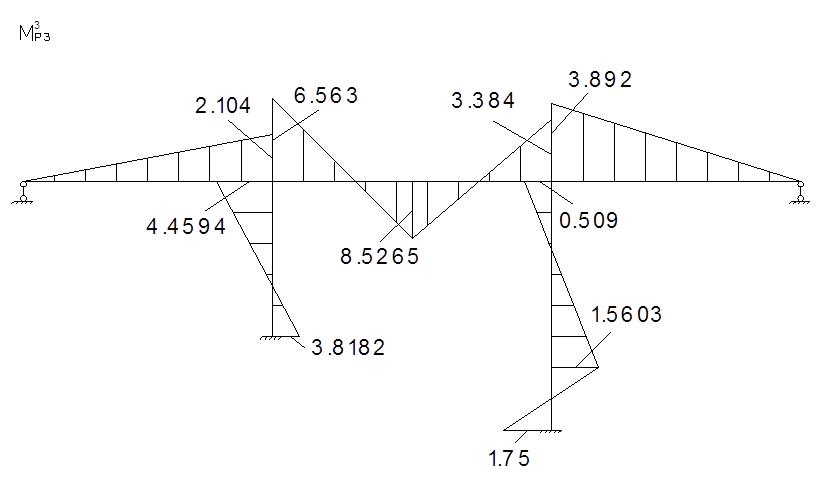
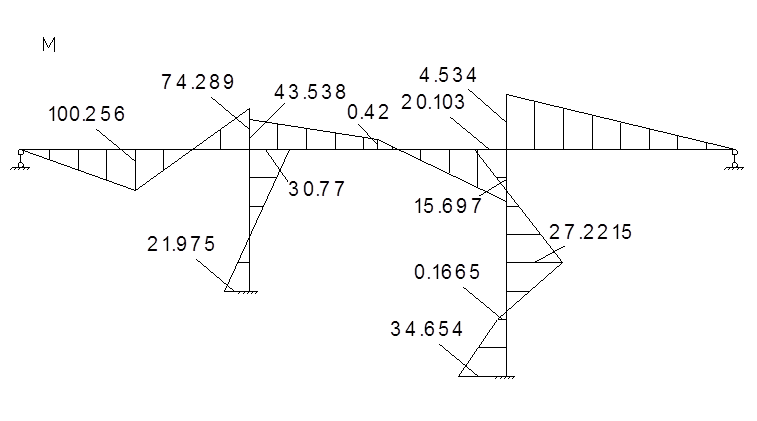
Строим окончательные эпюры моментов от воздействия инерционных сил.

- эпюра от динамических воздействий вибрационных сил и сил динамического воздействия.