|
Рис.8. Расчетная схема. |
Составим гипотезы раскрепления заготовки. Гипотеза 1. Проворот заготовки вокруг оси под действием силы Гипотеза 2. Опрокидывание заготовки относительно
точки |
![]() .
.
Отсюда находим, что 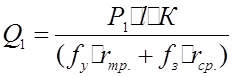 . Для второй гипотезы имеем
соответственно:
. Для второй гипотезы имеем
соответственно: ![]() или:
или: 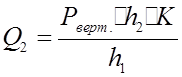 . Из двух принимаем
максимальную силу
. Из двух принимаем
максимальную силу ![]() и по ней определяем
диаметр цилиндра:
и по ней определяем
диаметр цилиндра: 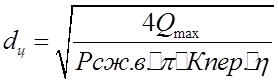 . В данном конкретном
случае
. В данном конкретном
случае ![]() , так как зажим заготовки
производится напрямую штоком. Здесь следует отметить, что ввиду небольшого
различия диаметров поверхности трения закрепления в расчете принят средний
радиус трения
, так как зажим заготовки
производится напрямую штоком. Здесь следует отметить, что ввиду небольшого
различия диаметров поверхности трения закрепления в расчете принят средний
радиус трения ![]() , а для поверхности
трения установки принят радиус трения
, а для поверхности
трения установки принят радиус трения ![]() ,
так как диаметры
,
так как диаметры ![]() отличаются
значительно. При этом радиус трения рассчитывают по зависимости:
отличаются
значительно. При этом радиус трения рассчитывают по зависимости:
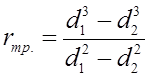 .
.
Следует иметь в виду тот факт, что
если в конструкции приспособления имеются пружины (пневматические цилиндры
одностороннего действия, автоматическое отбрасывание прихватов и т.д.) то
усилие ![]() необходимо увеличивать на
величину силы, воспринимаемой пружиной.
необходимо увеличивать на
величину силы, воспринимаемой пружиной.
2.5 Пример расчета приспособления на точность
Произведем расчет приспособления для
шпоночно-фрезерной операции при выполнении размера ![]() .
.
Минимальное условие
обеспечения точности обработки с применением приспособления имеет вид: ![]() , где
, где ![]() - коэффициент ужесточения
точности (
- коэффициент ужесточения
точности (![]() );
); ![]() -
допустимая погрешность установки заготовки.В нашем случае:
-
допустимая погрешность установки заготовки.В нашем случае: ![]() . Составляющие погрешности установки
. Составляющие погрешности установки
![]() представляют собой поля
рассеивания случайных величин распределение которых с достаточной
достоверностью можно принять подчиняющемуся нормальному закону. Тогда
погрешность установки определяется как суммарное поле рассеивания и
представляет собой случайную величину, подчиняющуюся также нормальному закону.
Значение
представляют собой поля
рассеивания случайных величин распределение которых с достаточной
достоверностью можно принять подчиняющемуся нормальному закону. Тогда
погрешность установки определяется как суммарное поле рассеивания и
представляет собой случайную величину, подчиняющуюся также нормальному закону.
Значение ![]() определяется по зависимости:
определяется по зависимости: ![]() , где
, где ![]() -представляют собой погрешности
базирования, закрепления и приспособления соответственно. Для случая установке
заготовки в призме погрешность базирования определится из выражения [ 6,
табл.18, с.45 ]:
-представляют собой погрешности
базирования, закрепления и приспособления соответственно. Для случая установке
заготовки в призме погрешность базирования определится из выражения [ 6,
табл.18, с.45 ]: 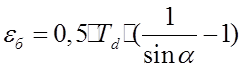 Здесь допуск на базовый
диаметр вала
Здесь допуск на базовый
диаметр вала![]() . Тогда имеем, что
. Тогда имеем, что 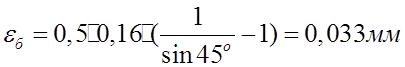 . Что касается погрешности
закрепления, то при использовании пневматического зажима (
. Что касается погрешности
закрепления, то при использовании пневматического зажима (![]() ) она будет равна нулю, т.е.
) она будет равна нулю, т.е. ![]() . Погрешность приспособления
определяется из выражения:
. Погрешность приспособления
определяется из выражения: ![]() , где
, где ![]() - погрешности изготовления,
износа и положения приспособления соответственно. Погрешность изготовления
приспособления рекомендуется принимать из выражения:
- погрешности изготовления,
износа и положения приспособления соответственно. Погрешность изготовления
приспособления рекомендуется принимать из выражения:![]() .
Здесь
.
Здесь ![]() - допуск на выполняемый
размер. В нашем случае примем
- допуск на выполняемый
размер. В нашем случае примем 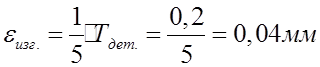 .
Допустимый износ
.
Допустимый износ ![]() принимают равным
величине
принимают равным
величине ![]() , т.е.
, т.е. ![]() Погрешность положения
определяется погрешностью используемых измерительных средств и обычно находится
в пределах:
Погрешность положения
определяется погрешностью используемых измерительных средств и обычно находится
в пределах: ![]() . Принимаем, что
. Принимаем, что ![]() . Тогда:
. Тогда: ![]() . Или окончательно:
. Или окончательно: ![]() . Таким образом, условие точности
выполняется (0,065<0,1мм.).
. Таким образом, условие точности
выполняется (0,065<0,1мм.).
Определим период нормальной
эксплуатации приспособления (или его установочных элементов) учитывая, что
накопленный износ ![]() в общем случае равен:
в общем случае равен:
![]() , где β — коэффициент интенсивности износа зависящий от вида
контакта и типа опоры; N —
число контактов заготовок с опорой в течение срока ее эксплуатации.
, где β — коэффициент интенсивности износа зависящий от вида
контакта и типа опоры; N —
число контактов заготовок с опорой в течение срока ее эксплуатации.
Интенсивность износа
опорных элементов возрастает при уменьшении площади их контакта, при наличии
на базовой поверхности заготовки следов литейного песка и окалины, если имеет
место «протаскивание» заготовки на опорах. Значения β приводятся в справочниках. Так для опор со сферической
головкой β=0,5÷2; при установке на
цилиндрические пальцы β=0,05÷0,1;
при установке на срезанные ромбические пальцы –β=0,02÷0,06; при установке на призму ![]() и т. Таким образом, допустимое
число контактов заготовок с приспособлением равно:
и т. Таким образом, допустимое
число контактов заготовок с приспособлением равно: .
Для нашего примера имеем:
.
Для нашего примера имеем:  шт. При
годовой программе
шт. При
годовой программе ![]() период
период ![]() эксплуатации приспособления
будет равен:
эксплуатации приспособления
будет равен: 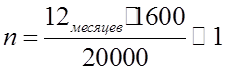 месяц.
месяц.
2.6 . Расчет опасных элементов приспособления на прочность.
Допустим что в приспособлении наиболее опасными элементами конструкции являются прихват в месте где имеется отверстие для тяги, ось ролика и болты крепления кондукторной плиты ( два болта). Произведем их проверку на прочность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.