Гипотезы раскрепления заготовки. Уравнение статического равновесия заготовки. Расчет необходимого диаметра пневмо – гидроцилиндра, страница 3

Где  и - плечи действия сил  и  соответственно. Отсюда имеем: 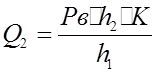                                                  (9)

Гипотеза 3.Уравнение статического равновесия можно записать сразу в силовом выражении (см. рис.4):

Рис.3. К гипотезе 2.

Рис.4. К гипотезе 3.

. Здесь силы  аналогичны гипотезе 1. Тогда имеем: . Отсюда имеем: 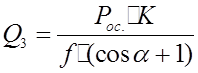                   (10)

Здесь следует отметить, что если коэффициенты трения установки и закрепления не равны друг другу, то следует пользоваться выражением:

.

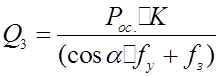После расчета главной составляющей силы резания [7, с. 281-292] находим остальные составляющие  силы резания (см. табл. 42, с. 292.). Подставив их значения в формулы 7,8 и 9 имеем численные значения. Из трех полученных сил выбираем максимальную по величине

() и по ней ведем расчет диаметра цилиндра по формуле (4):

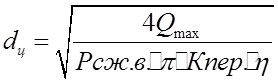
Как видно из приведенного выше расчета варьировать значениями можно путем изменения угла призмы  и коэффициентов трения  и . Например, при использовании рифленых установочных и зажимных поверхностей значение увеличивается в несколько раз.

2.2.  Применительно к фрезерно - центровальной операции.

Поскольку на этой технологической операции обработки вала предусмотрен технологический переход на котором производится изготовление центровых отверстий, то для базирования заготовки наиболее целесообразно использовать скрытую (условную) базу – ось детали. Поэтому часто для базирования и закрепления заготовки в этом случае используют самоцентрирующие призмы (рис.5 и 6), которые позволяют обеспечивать максимально возможную соосность оси заготовки с осью вращения центровочных сверл. На рисунках показаны силы, действующие на заготовку. Составим гипотезы ее раскрепления.

Гипотеза 1. Проворот заготовки вокруг своей оси под действием главной составляющей силы резания ;

Гипотеза 2. Раскрытие призм под действием сил  и ;

Рис.5. Схема обработки.

Гипотеза 3. Сдвиг заготовки вдоль оси. Данная гипотеза отбрасывается, так как силы  при одновременной работе двух фрез практически взаимно уравновешиваются.

Рис.6 Расчетная схема.

Таким образом, первые две гипотезы принимаем в качестве рабочих. Запишем уравнение равновесия для первой гипотезы:  или: . Так как в данном случае , то . Отсюда имеем:

.

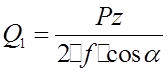Для второй гипотезы уравнение равновесия имеет вид:

 или:  (см. рис.6).

Отсюда окончательно имеем: .

Как и в предыдущем случае выбираем из двух максимальную силу и по ней рассчитываем диаметр цилиндра: 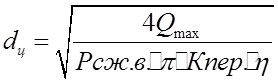. Следует иметь в виду, что при симметричном торцовом фрезеровании составляющие силы резания  и  ([7,табл. 42, с. 292]).

2.3.  Применительно к токарной и круглошлифовальной операциям.

На этих операциях валы и зубчатые колеса часто устанавливаются в самоцентрирующих патронах (например, кулачковых и цанговых).

Рис.7. Закрепление заготовки в самоцентрирующем патроне.

На заготовку действует крутящий момент и осевая составляющая силы резания (см. рис.7.). Составим гипотезы раскрепления заготовки:

Гипотеза 1. Проворот заготовки под действием .

Гипотеза 2. Сдвиг заготовки вдоль оси. Эту гипотезу исключаем из рассмотрения, так как заготовка упирается в торец патрона или кулачков.

Запишем уравнение равновесия для первой (рабочей) гипотезы:

. Раскрывая правую часть уравнения, имеем:. Отсюда получаем, что: . В итоге расчетов имеем: ; .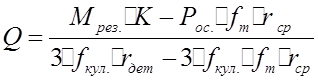

В случае применения цанговых патронов формулы для расчета усилий зажима приведены в литературе, например, /4, с. 241-243/.

2.4.  Применительно к зубофрезерной операции.

На этой операции производится нарезание зубьев шестерни или зубчатого колеса долбяком или червячной фрезой. На рис.8 представлена одна из возможных принципиальных схем установки заготовки при нарезании зубьев шестерни. При этом на заготовку действуют вертикальная и касательная к окружности (перпендикулярно плоскости чертежа) силы.