1. Выбрать задачу в соответствии со своим номером.
2. Написать математическую модель прямой задачи, указав экономический смысл всех переменных.
3. Подготовить данные в Excel и провести расчет задачи.
4. Проанализировать полученный результат.
1. Задача. На некоторой фирме для производства двух видов товаров в количестве Х и Y используются два вида взаимозаменяемых ресурсов – труд(L) и капитал (K.), объем которых ограничен значениями L0 = 15 и K0 = 12 соответственно. Определить наиболее выгодное для фирмы распределение ресурсов, если цены товаров равны соответственно Р1 = 5,7 и Р2. = 6,0
Принимая, что издержки производства постоянны, задача сводится к задаче о максимуме функции дохода.
В качестве модельных производственных функций обоих товаров рассмотреть производственные функции типа Кобба-Дугласа с параметрами a = 0,6, b = 0,4, c = 0,8, d = 0,2.
2. Математическая модель задачи:
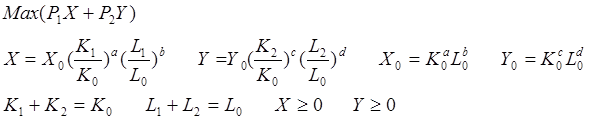
где X0, Y0 –максимальные значения выпуска товаров при заданных ограничениях на ресурсы.
Для анализа производственных функций следует рассмотреть изокванты (линии равных уровней производства товара) на диаграмме Эджуорта-Боули, для чего берется прямоугольник со сторонами равными объемам ресурсов K0 и L0. В нижнем левом углу прямоугольника находится начало координатных осей K1 и L1, а в верхнем правом его углу – начало координат осей K2 и L2. Особенностью “ящика Эджуорта” является то, что в нем автоматически выполняются два балансовых ограничения на ресурсы.
При построении изоквант производственной функции товара Х = Х* и Y = Y* будем использовать формулы :
![]()
3. Заполним расчетные таблицы в Excel.
В ячейки B9:B10 введем цены продуктов, в ячейки F9:G10 – соответствующие коэффициенты производственных функций обоих продуктов, в ячейки D11:E11 ограничения на объемы капитала и труда.
В ячейку Н9 введем формулу =ЕСЛИ(И(D9>0;E9>0);I9*(D9/D$12)^F9*(E9/E$12)^G9;0) которую скопируем вячейку Н10. В ячейку I9 введем формулу =ЕСЛИ(И(D9>0;E9>0);D$12^F9*E$12^G9;0), которую скопируем вячейку I10. В ячейку D11 введем формулу =D9+D10, которую скопируем вячейку E11.
Для анализа двойственности в ячейку D13 введем формулу =H12, в ячейку E13 введем формулу =H13, в ячейку D16 введем формулу =D13*(D9+D10)+E13*(E9+E10).
В ячейке D15 находится формула =СУММПРОИЗВ(H9:H10;C9:C10), которая вычисляет целевую функцию задачи.
Переходим к поиску решения задачи. Поставив курсор в ячейку D15, выберем пункт меню СЕРВИС-ПОИСК РЕШЕНИЯ. Заполняем входные данные целевая функция D15
максимум изменяемые ячейки F9:G10 ограничения D9:E11 >= 0
D11:E11 = D12:E12
Выполнить тип отчета Устойчивость OK
Переходим на лист “Отчет по устойчивости”, копируем “Множители Лагранжа” из ячеек E17:E18, возвращаемся в текущий лист и вставляем скопированные ячейки в H12:H13. После этого возвращаемся и удаляем лист “Отчет по устойчивости”. В результате расчета получим таблицу, представленную ниже.
4. Анализ результатов.
Максимальная прибыль в объеме 76,89 д.е получается при выпуске 6,057 ед первого продукта и 7,061 ед. второго продукта. При этом двойственные оценки ресурсов дают суммарную оценку сырья в объеме равном полученной прибыли, что соответствует первой теореме двойственности.
Для анализа самой производственных функций, создадим таблицы значений двух изоквант первой производственной функции при значении X = X* и второй производственной функции для значения Y = Y*. В ячейку C19 вводим формулу =H9, вячейку E19=H10. В ячейку B21 вводим формулу =1, в ячейку C21- =E$12*(C$19
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.