Модель Солоу. Схема функционирования экономики согласно модели Солоу. Переходный режим модели Солоу

РГЗ

Тема “Модель Солоу”

Порядок работы

1.  Выбрать задачу в соответствии со своим номером.

2.  Написать математическую модель, указав экономический смысл всех переменных.

3.  Подготовить данные в Excel и провести расчет  задачи.

4.  Проанализировать полученный результат.

1. Теоретический материал

Модель Солоу

Модель Солоу является односекторной моделью экономического роста. в этой модели экономическая система рассматривается, как единое целое, производит универсальный продукт, который может потребляться так и инвестироваться. Модель достаточно адекватно отражает важнейшие макроэкономические аспекты процесса воспроизводства. Экспорт-импорт в явном виде в явном виде не учитывается.

Состояние экономики в модели Солоу задается следующими пятью эндогенными переменными: X - валовой общественный продукт (ВОП), С - фонд непроизводственною потребления, I - инвестиции, L - число занятых, К - фонды. Кроме того, в модели используются следующие экзогенные (заданные вне системы) показатели: n - годовoй темп прироста числа занятых, m - доля выбывших за год основных производственных фондов, a - коэффициент прямых затрат (доля промежуточною продукта в ВОП), r - норма накопления (доля валовых инвестиций в валовом внутреннем продукте). Экзогенные параметры находятся в следующих границах:

-1<n<1, 0<m<1, 0<a<1,0<r<1.

Предполагается, что эндогенные переменные изменяются во времени (аргумент t опущен, но присутствует по умолчанию). Экзогенные переменные считаются постоянными во времени, причём норма накопления является управляющим параметром, т.е. в начальный момент времени может устанавливаться управляющим органом системы на любом уровне из области допустимых значений.

Время считается непрерывным и измеряется в годах. Для мгновенных показателей L=L(t), K=K(t) это представляется совершенно естественным, поскольку в любой день можно установить число занятых и путём инвентаризации объём основных производственных фондов. Значения показателей потока X=X(t), I=I(t), C=C(t) в момент t=[t]+{t} определяются в виде накопленных за год, начинающихся на 365{t} дней позже 1 января года [t].

Предполагается, что годовой выпуск в каждый момент времени определятся линейно-однородной функцией неокласической функцией:

X=F(K,L).

Рассмотрим как меняются ресурсные показатели за небольшой промежуток времени Dt. Согласно определению темпа прироста:

   или  

поэтому

, 

Используя начальное условие L(0)=L_o, получаем:

износ и инвестиции в расчёте на год равны m×Kи I соответсвенно, а за время Dt – соотвественно m×K×Dt, I×Dt, поэтому прирост фондов за это время:

DK=-m×K×Dt+I×Dt, откуда получаем дифференциальное уравнение:

Поскольку промежуточный продукт равен a×X, то валовый внутренний продукт равен (1-a)X, в том числе инвестиции I=r(1-a)X и фонд потребления C=(1-r)(1-a)X.

Получим следующую запись модели Солоу в абсолютных показателях:

На рисунке приведена схема функционирования экономики согласно модели Солоу.

 

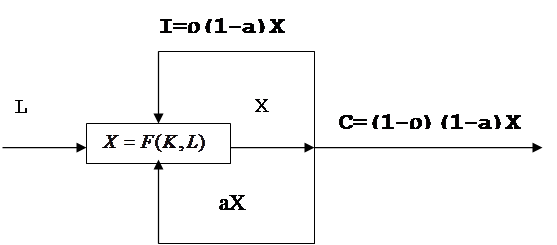Введём следующие относительные показатели:

 - фондовооружённость;

 - народохозяйственная производительность труда;

 - удельные инвестиции;

 - среднедушевое потребление (на одного занятого).

Между относительными и абсолютными показателями можно установить следующую связь:

Тогда модель Солоу в удельных показателях приобретает следующий вид:

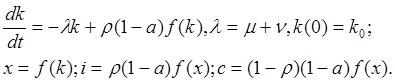
Таким образом, каждый  абсолютный или относительный показатель изменяется во времени, т.е. можно говорить о траектории системы в абсолютных или относительных показателях.

Траектория называется стационарной, если показатели не изменяются во времени:

Исходя из модели Солоу в удельных показателях видно, что установление фондовооружённости на постоянном уровне приводит к выводу на стационарную траекторию. На стационарной траектории , поэтому:

В качестве функции F(K,L) – неоклассическая , то f(0)=0, f^/>0,f^//<0. Если ещё задать условие

, то уравнение будет иметь единственное ненулевое решение, что видно из графика:

 

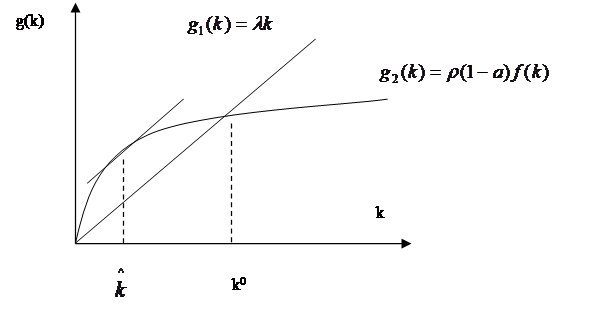При этом через  обозначена фондовооружённость при которой скорости роста функций g₁(k) и g₂(k) одинаковы.

Переходный режим модели Солоу.

Если k₀=k⁰, то экономика уже находиться на стационарной траектории и может сойти с неё только при изменении внешних условий.

При k₀¹k⁰ в экономике будет происходить переходный процесс, который закончится установлением стационарного режима. В переходном режиме фондовооружённость удовлетворяет уравнению:

Причём из последнего рисунка видно