Длина вектора ![]() вычисляется
по формуле
вычисляется
по формуле
![]() .
.
Если ![]() , то вектор
, то вектор
![]() имеет координаты
имеет координаты
![]() .
.
Пусть ![]() . Тогда
. Тогда
![]() ,
, ![]() ,
, ![]() .
.
Косинусы углов, образованных вектором ![]() с положительными координатными
полуосями, называют направляющими косинусами вектора,
с положительными координатными
полуосями, называют направляющими косинусами вектора,
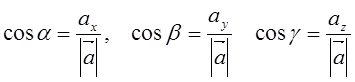 .
.
Вектор с координатами ![]() сонаправлен с вектором
сонаправлен с вектором ![]() и имеет единичную длину.
и имеет единичную длину.
Скалярным произведением вектора ![]() на вектор
на вектор ![]() называют число, обозначаемое
называют число, обозначаемое ![]() ,
,
![]() , где
, где ![]() – угол между векторами
– угол между векторами ![]() и
и ![]() .
Если даны координаты векторов, то скалярное произведение можно вычислить
следующим образом:
.
Если даны координаты векторов, то скалярное произведение можно вычислить
следующим образом:
![]() .
.
Угол между векторами можно найти, используя формулу
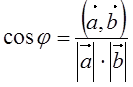 .
.
Свойства скалярного произведения.
![]()
![]()
![]()
![]()
![]() .
.
Векторным произведением вектора ![]() на вектор
на вектор ![]() называют вектор
называют вектор ![]() со свойствами:
со свойствами:
![]()
![]()
![]() Векторы
Векторы
![]() образуют правую тройку.
образуют правую тройку.
Векторное произведение вектора ![]() на вектор
на вектор ![]() обозначают
обозначают ![]()
Свойства векторного произведения
![]() ;
;
![]()
![]()
![]()
Векторное произведение можно вычислить по формуле:
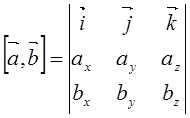 .
.
Пример 1. ![]() . Найти направляющие косинусы
вектора
. Найти направляющие косинусы
вектора ![]() .
.
Решение. ![]() .
.
![]() .
.
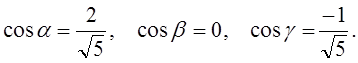
Пример 2. Векторы ![]() неколлинеарные, т.к.
коллинеарность означает линейную зависимость этих векторов:
неколлинеарные, т.к.
коллинеарность означает линейную зависимость этих векторов: ![]() , т.е.
, т.е. 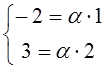 . Полученная система очевидно
несовместна. Поэтому можно утверждать, что векторы
. Полученная система очевидно
несовместна. Поэтому можно утверждать, что векторы ![]() и
и
![]() образуют базис на
плоскости. Пусть
образуют базис на
плоскости. Пусть ![]() . Разложить вектор
. Разложить вектор ![]() по базису
по базису ![]() .
.
Решение. 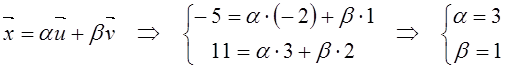 .
.
Следовательно, вектор ![]() имеет в базисе
имеет в базисе ![]() координаты
координаты ![]() .
.
Пример 3. Даны точки ![]() . Найти косинус
. Найти косинус ![]() .
.
Решение. 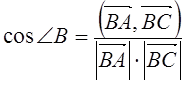 .
.
![]() ,
,
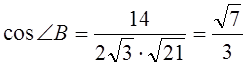 .
.
Пример 4. Даны точки ![]() . Найти площадь треугольника
. Найти площадь треугольника ![]() .
.
Решение. ![]()
![]() .
.
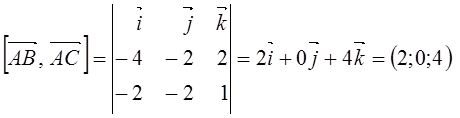 .
.
![]() .
.
1. Векторы
![]() и
и![]() заданы
геометрически. Построить векторы
заданы
геометрически. Построить векторы ![]()
2. Пусть
![]() В
В![]() каком
случае вектор
каком
случае вектор ![]() параллелен
биссектрисе угла в треугольнике
параллелен
биссектрисе угла в треугольнике![]() ?
?
3. В
треугольнике ![]()
![]() записать
какой-либо вектор, параллельный биссектрисе угла
записать
какой-либо вектор, параллельный биссектрисе угла ![]() .
.
4. Найти длину вектора ![]() если:
если:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
5. Найти координаты вектора ![]() если:
если:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
6. Найти координаты точки![]() , если:
, если:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
7. Пусть ![]() . Проверить справедливость равенства
. Проверить справедливость равенства
![]() .
.
8. Вычислить направляющие косинусы
векторов ![]() .
.
9. Найти координаты векторов ![]() , если:
, если:
![]()
![]()
![]() .
.
10. При каком ![]() коллинеарны векторы
коллинеарны векторы ![]() и
и ![]() ?
?
1)
![]()
![]()
2)
![]()
3)
![]()
11. Убедиться в том, что векторы ![]() ,
, ![]() образуют
базис на плоскости. Найти разложение по базису
образуют
базис на плоскости. Найти разложение по базису ![]() и
и
![]() векторов
векторов ![]()
12. Найти скалярное произведение
векторов ![]() и
и ![]() , образующих угол
, образующих угол ![]() :
:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
13. Известно, что ![]() Вычислить скалярные
произведения векторов:
Вычислить скалярные
произведения векторов:
![]()
14. Вычислить
скалярное произведение векторов ![]() и
и ![]() :
:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
15.
Вычислить угол между векторами ![]() и
и ![]() :
:
1)
![]()
2)
![]()
3)
![]() .
.
16. Вычислить, при каком ![]() векторы
векторы ![]() и
и ![]() перпендикулярны:
перпендикулярны:
1)
![]()
2)
![]()
17. Найти углы треугольника ![]() , если:
, если:
1)
![]()
2)
![]()
18. Вычислить ![]() если:
если:
1)
![]() и угол между ними
и угол между ними ![]() ;
;
2)
![]()
3)
![]()
4)
![]()
19. Вычислить ![]() и
и ![]() ,
если:
,
если:
1)
![]()
2)
![]()
3)
![]()
20. Найти площадь треугольника![]() , если:
, если:
1)
![]()
![]()
2)
![]()
3)
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.