титульном листе должны быть указаны
следующие данные: кафедра, дисциплина, вариант, специальность, курс, фамилия,
имя, отчество, идентификатор.
Каждый обучаемый выбирает номер
варианта в соответствии с тремя последними цифрами
идентификатора. Если идентификатор (три последние цифры) больше количества
вариантов заданий, то номер варианта рассчитывается делением идентификатора
(три последние цифры) на количество вариантов и остаток от деления –
это Ваш вариант. Если остаток от деления равен нулю, то Ваш вариант
соответствует последнему номеру варианта лабораторной работы. (Пример.
Идентификатор – m02e1g1-025. Количество вариантов – 14. Расчет: 25:14=1 с остатком
11. Ваш вариант – 11).
При наличии пакета Математика 4 на компьютере, полученный
окончательный численный результат решения заданий лабораторной работы должен
быть проверен при помощи пакета Математика 4. В случае совпадения
численных результатов, работа и проверочный файл пакета Математика 4
должны быть представлены тьютору для зачета.
Решение необходимо оформлять при
помощи компьютерных редакторов и представлять в электронном виде для
регистрации на учебном Web-сайте.Обязательное требование - имя отчетного файла должно содержать только латинские символы (пример:lab3vmat.doc).
Вариант 1
1. Исследовать сходимость рядов:
|
1. 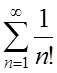 ; ;
|
2. 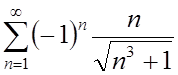 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
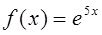
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
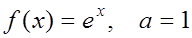
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
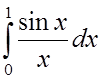
5. Найти решение задачи Коши:
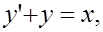
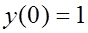
6. Найти общее решение уравнения:
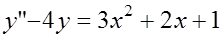
Вариант 2
1. Исследовать сходимость рядов:
|
1. 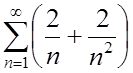 ; ;
|
2. 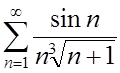 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
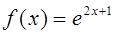
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
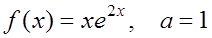
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
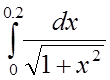
5. Найти решение задачи Коши:
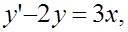
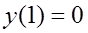
6. Найти общее решение уравнения:
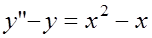
Вариант 3
1. Исследовать сходимость рядов:
|
1. 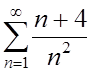 ; ;
|
2. 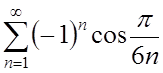 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
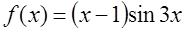
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
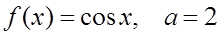
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
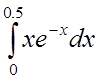
5. Найти решение задачи Коши:
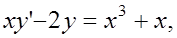
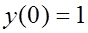
6. Найти общее решение уравнения:
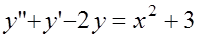
Вариант 4
1. Исследовать сходимость рядов:
|
1. 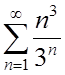 ; ;
|
2. 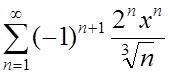 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
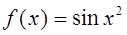
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
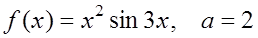
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
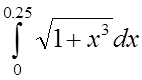
5. Найти решение задачи Коши:
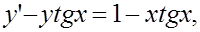
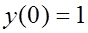
6. Найти общее решение уравнения:
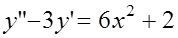
Вариант 5
1. Исследовать сходимость рядов:
|
1. 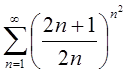 ; ;
|
2. 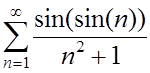 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
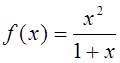
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
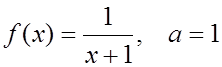
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
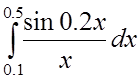
5. Найти решение задачи Коши:
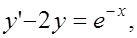
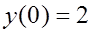
6. Найти общее решение уравнения:
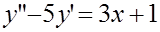
Вариант 6
1. Исследовать сходимость рядов:
|
1. 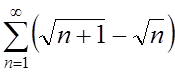 ; ;
|
2. 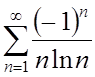 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
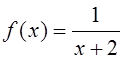
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
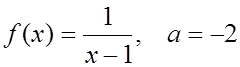
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
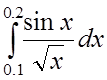
5. Найти решение задачи Коши:
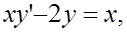
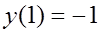
6. Найти общее решение уравнения:
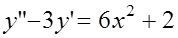
Вариант 7
1. Исследовать сходимость рядов:
|
1. 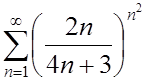 ; ;
|
2. 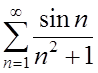 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество сходимости ряда:
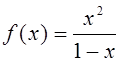
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
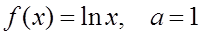
4. Используя разложение в ряд подынтегральной
функции, вычислить с точностью до 0,0001 интеграл :
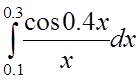
5. Найти решение задачи Коши:
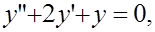
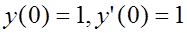
6. Найти общее решение уравнения:
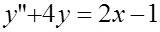
Вариант 8
1. Исследовать сходимость рядов:
|
1. 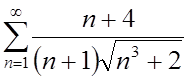 ; ;
|
2. 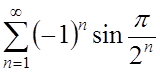 ; ;
|
2. Разложить в степенной ряд по степеням функцию f(x)
и найти множество
![]()
![]()
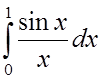
![]()
![]()
![]()
![]()
![]()
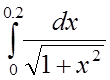
![]()
![]()
![]()
![]()
![]()
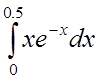
![]()
![]()
![]()
![]()
![]()
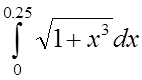
![]()
![]()
![]()
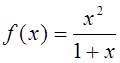
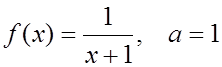
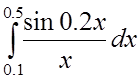
![]()
![]()
![]()
![]()
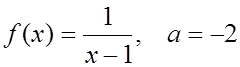
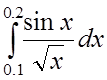
![]()
![]()
![]()
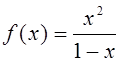
![]()
![]()
![]()
![]()