каждого полностью охваченного блока (подшипники скольжения или качения) |
0,91-0,95 |
|
|
Клиновые ремни |
Для каждого полностью охваченного шкива (нормальное натяжение ремня) |
0,88-0,93 |
|
Полимерные ленты |
Для каждого полного обхвата/барабаны на подшипниках качения (нормальное натяжени ленты) |
0,81-0,85 |
|
Зубчатые ремни |
Для каждого полного обхвата/шкивы на подшипниках качения (нормальное натяжение ремня) |
0,90-0,96 |
|
Цепи |
Для каждого полного обхвата/звездочки на подшипниках качения (в зависимости от размера цепи) |
0,90-0,96 |
|
Редукторы |
Смазка маслом, 3 ступени (цилиндрические шестерни), в зависимости от качества изготовления |
0,94-0,97 |
|
Ходовой винт |
Трапецеидальная резьба (в зависимости от шага и смазки) |
0,3-0,5 |
|
Шариковый ходовой винт |
0,8-0,9 |
Уравнения движения электропривода
Механическая часть электропривода представляет собой систему твердых тел, на движение которых наложены ограничения, определяемые механическими связями. Уравнения механических связей устанавливают соотношения между перемещениями в системе, а в тех случаях, когда задаются соотношения между скоростями ее элементов. Наиболее общей формой записи дифференциальных уравнений движения таких систем являются уравнения движения в обобщенных координатах (уравнения Лагранжа);
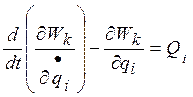 ,
(2-7)
,
(2-7)
где
![]() -
запас кинетической энергии системы, выраженный через обобщенные координаты
-
запас кинетической энергии системы, выраженный через обобщенные координаты ![]() и
обобщенные скорости
и
обобщенные скорости ![]() ;
;
![]() - обобщенная
сила, определяемая суммой элементарных работ
- обобщенная
сила, определяемая суммой элементарных работ ![]() всех
действующих сил на возможном перемещении
всех
действующих сил на возможном перемещении ![]()
или
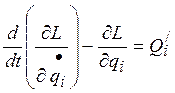 ,
(2-8)
,
(2-8)
где
L — функция
Лагранжа; ![]() —
обобщенная сила, определяемая суммой элементарных работ
—
обобщенная сила, определяемая суммой элементарных работ ![]() всех
внешних сил на возможном перемещении
всех
внешних сил на возможном перемещении ![]() .
.
Функция
Лагранжа представляет собой разность кинетической ![]() и
потенциальной
и
потенциальной ![]() энергий
системы, выраженных через обобщенные координаты
энергий
системы, выраженных через обобщенные координаты ![]() и
обобщенные скорости
и
обобщенные скорости ![]() ,
т. е.
,
т. е.
![]() .
(2-9)
.
(2-9)
Уравнения Лагранжа дают единый и достаточно простой метод математического описания динамических процессов в механической части привода; их число определяется только числом степеней свободы системы.
В качестве обобщенных координат могут быть приняты как различные угловые, так и линейные перемещения в системе. Поэтому при математическом описании динамики механической части привода с помощью уравнений Лагранжа предварительного приведения всех ее элементов к одной скорости не требуется. Однако, как было отмечено, до выполнения операции приведения в большинстве случаев невозможно количественно сопоставлять между собой различные массы системы и жесткости связей между ними, следовательно, невозможно выделить главные массы, главные упругие связи, определяющие минимальное число степеней свободы системы, подлежащее учету при проектировании. Поэтому составление приведенных расчетных механических схем и их возможное упрощение являются первым важным этапом расчета сложных электромеханических систем электропривода независимо от способа получения их математического описания
Получим
уравнения движения, соответствующие обобщенным расчетным механическим схемам
электропривода, представленным на рис.1- 6. В трехмассовой упругой системе
обобщенными координатами являются угловые перемещения масс ![]()
![]() , им соответствуют
обобщенные скорости
, им соответствуют
обобщенные скорости ![]() .Функция
Лагранжа имеет вид:
.Функция
Лагранжа имеет вид:
![]()
(2-10)
Для
определения обобщенной силы ![]() необходимо
вычислить элементарную работу всех приложенных к первой массе моментов на
возможном перемещении:
необходимо
вычислить элементарную работу всех приложенных к первой массе моментов на
возможном перемещении:
![]() ;
(2-11)
;
(2-11)
Следовательно,
![]() . (2-12)
. (2-12)
Аналогично определяются две другие обобщенные силы
![]() ;
; ![]() .
(2-13)
.
(2-13)
Подставляя (2-10) в (2-8) и учитывая (2-12) и (2-13), получаем следующую систему уравнений движения:
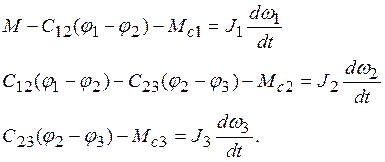 (2-14)
(2-14)
В (2-14) пропорциональные деформациям упругих связей моменты являются моментами упругого взаимодействия между движущимися массами системы:
![]()
![]() .
(2-15)
.
(2-15)
С учетом (2-15) систему уравнений движения можно представить в виде
![]()
![]() (2-16)
(2-16)
![]()
Рассматривая (2-16), можно установить, что уравнения движения приведенных масс электропривода однотипны. Они отражают физический закон (второй закон Ньютона), в соответствии с которым ускорение твердого тела пропорционально сумме всех приложенных к нему моментов (или сил), включая моменты и силы, обусловленные упругим взаимодействием с другими твердыми телами системы.
Уравнения
движения двухмассовой системы могут быть получены из (2-16) если положить ![]() и
и ![]()
![]()
![]() (2-17)
(2-17)
где
![]() .
.
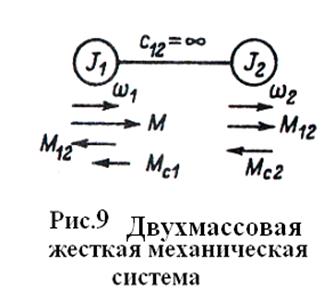 Переход
от двухмассовой упругой системы к эквивалентному жесткому приведенному
механическому звену для большей наглядности полезно выполнить в два этапа. Считая
механическую связь между первой и второй массами (см. рис.1-6) абсолютно
жесткой (
Переход
от двухмассовой упругой системы к эквивалентному жесткому приведенному
механическому звену для большей наглядности полезно выполнить в два этапа. Считая
механическую связь между первой и второй массами (см. рис.1-6) абсолютно
жесткой (![]() ), получим
двухмассовую жесткую систему, расчетная
), получим
двухмассовую жесткую систему, расчетная
 схема которой
показана на рис.2-1. Отличием ее от схемы на рис. 6, б является равенство
скоростей масс
схема которой
показана на рис.2-1. Отличием ее от схемы на рис. 6, б является равенство
скоростей масс ![]() при
этом в соответствии
при
этом в соответствии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.