Режимы работы и характеристики шаговых двигателей. Статический синхронизирующий момент. Зависимости синхронизирующего момента парового двигателя

Лекция 17

РЕЖИМЫ РАБОТЫ И ХАРАКТЕРИСТИКИ ШАГОВЫХ

ДВИГАТЕЛЕЙ

Работа шагового двигателя считается устойчивой, если он работает без потерь шага,  т.е.  если ротор переходит из одного  устойчивого состояния  в  другое при каждом шаге результирующего вектора м.д.с. обмоток управления. Характер движения ротора и многие величины, определяющие работу шагового двигателя,  зависят от частоты управляющих импульсов .  

 Статический режим  () характеризуется протеканием  постоянного тока по обмоткам управления шагового двигателя и неизменностью положения вектора  результирующей  м.д.с.  Основная  характеристика этого  режима  - зависимость синхронизирующего момента двигателя от электрического угла рассогласования  ,  т.е. угла между осью ротора и направлением вектора м.д.с.  управления. Для двигателей с симметричным ротором эта зависимость в первом приближении может быть принята синусоидальной, (рис. 11,а):

.

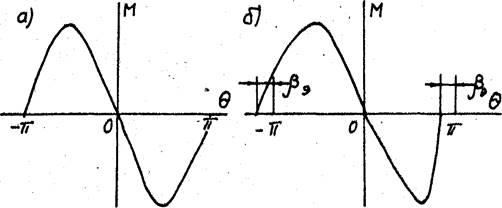
Рис. 11. Статический синхронизирующий момент: а – для симметричного ротора; б - для несимметричного

В двигателях с несимметричным ротором  кривая  синхронизирующего момента несимметрична (рис.  11,б).  Положительная и отрицательная полуволны кривой остаются равновеликими по площади, но имеют разную протяженность по оси  .

Поскольку при   синхронизирующий момент равен нулю, возникает статическая ошибка в положении ротора.  Величина этой ошибки зависит от момента нагрузки  и уменьшается с увеличением максимального момента двигателя  .

   Зоной статической устойчивости  называется  интервал  угловых положений ротора, в пределах которого ротор возвращается в исходное положение.  При нулевом статическом моменте точка статического равновесия – «0»,  а точки неустойчивого равновесия - А и В, т.е. зона статической устойчивости АОВ симметрична (рис. 12)

.

   При наличии статического момента зона статической  устойчивости становится несимметричной,  например,   при  и при.

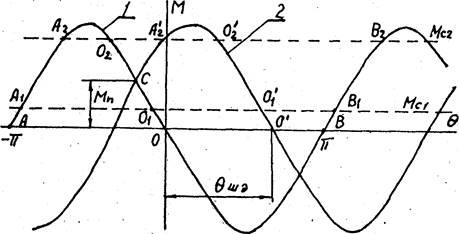Рис. 12. Зависимости синхронизирующего момента парового        двигателя от угла рассогласования  для двух устойчивых соседних положений

  Зоной динамической  устойчивости   называется интервал угловых положений ротора, определенный с учетом сдвига кривой синхронизирующего момента при очередном переключении обмоток.  Для шаговых двигателей с симметричным ротором

, и  для шаговых двигателей с несимметричным ротором

.

   Пусковым моментом шагового двигателя  называется максимальный момент нагрузки, при котором возможен пуск двигателя,  т.е. выполнение им шага в заданном направлении. Величина этого момента определяется точкой C пересечения исходной характеристики (кривая 1, рис.12) с характеристикой,  сдвинутой на один шаг (кривая 2, рис. 12). Если , то ротор (точка) при переключении обмоток управления  окажется  вне  зоны статической устойчивости  и пуска не произойдет.

Квазистатический режим  шагового двигателя  (режим отработки единичных шагов) соответствует частоте управляющих импульсов при которой переходный процесс на каждом шаге заканчивается к началу следующего шага,  т.е.  угловая скорость ротора  в начале каждого шага равна нулю (рис. 13).

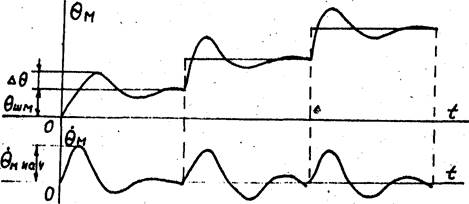Рис. 13  Переходные процессы в шаговом двигателе при отработке единичных шагов

Основными показателями этого режима  являются  перерегулирование,  максимальное значение угловой скорости ротора 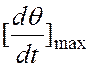и время затухания переходного процесса .   Установившийся режим  работы  шагового  двигателя  соответствует постоянной частоте управляющих импульсов, причем 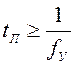. Вращение ротора с некоторой средней скоростью сопровождается колебаниями относительно точки устойчивого равновесия.  Амплитуда этих  колебаний достигает  наибольшего  значения при частоте управляющих импульсов,  совпадающей с собственной частотой колебаний ротора. Она находится из дифференциального уравнения движения ротора

.

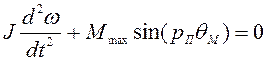Считая    малой величиной (в окрестности точки устойчивого равновесия), получим

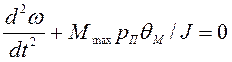
откуда                                                   .

Степень демпфирования колебаний ротора шагового двигателя  зависит  от момента сопротивления (сухого трения) и внутреннего демпфирования, обусловленного преобразованием механической энергии ротора в электромагнитную, т.е. за счет наведения э.д.с. вращения в обмотках управления, которая вызывает появление в них дополнительных токов.  Эти  токи,  взаимодействуя с вызвавшими их потоками,  создают  демпфирующий момент. В шаговых двигателях активного типа э.д.с. наводится  потоком  ротора,  в  индукторных и реактивных – переменной