Фазовые портреты нелинейной сау по скользящим режимам. Исследование системы с релейным элементом

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Систем Автоматического Управления

Отчет

По лабораторной работе №7

 «Фазовые портреты нелинейной сау по скользящим режимам»

Выполнили:

Группа  4083/12

Принял:   

Санкт-Петербург, 2011 г.

1.Исследование системы с релейным элементом

Схема эксперимента:

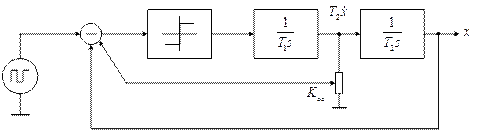
На вход схемы подаём сигнал прямоугольной формы с некоторой амплитудой.

В качестве нелинейности используется релейный элемент (РЭ) с уровнем .

В схеме также используются два интегратора на основе операционных усилителей

Параметры дополнительных элементов:

.

Теоретические параметры:

,

.

Практические параметры:

,

.

Обратная связь реализована через делитель напряжения, обеспечивающий передачу с коэффициентом .

В ходе эксперимента были исследованы фазовые портреты системы при различных значениях  в системе координат . Также были сняты графики зависимостей  и . Было выделено 4 основных фазы изменения картины:

1):

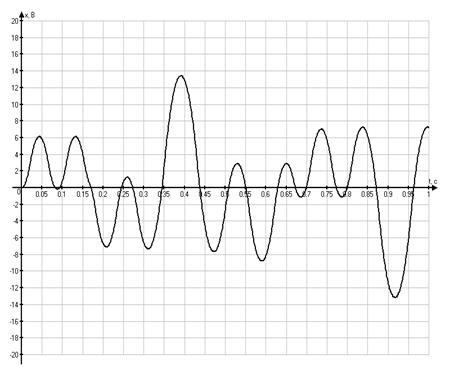
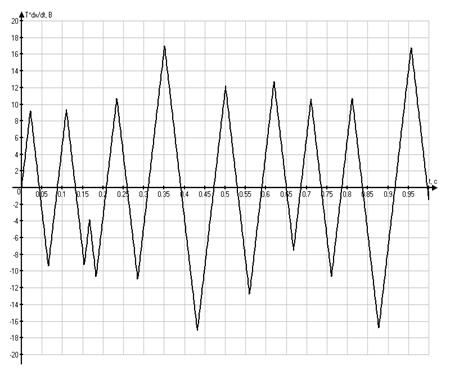
Графики временных зависимостей  и , соответственно

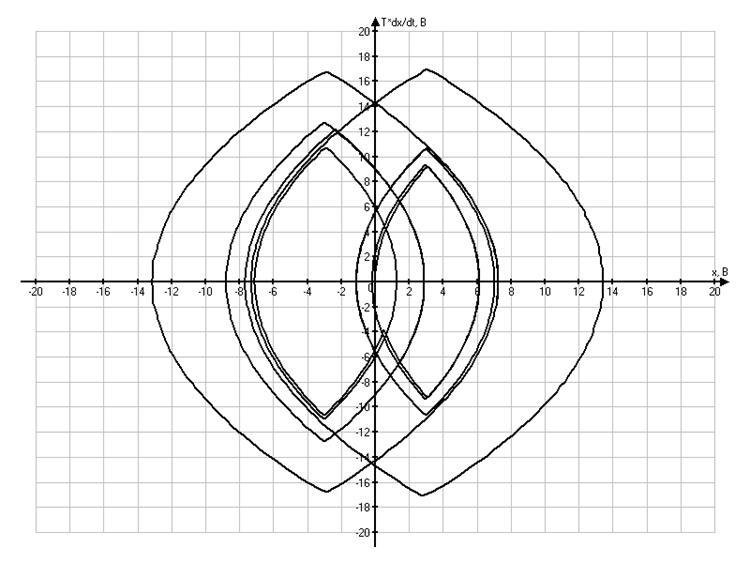
Фазовый портрет в системе координат

2):

Графики временных зависимостей  и , соответственно

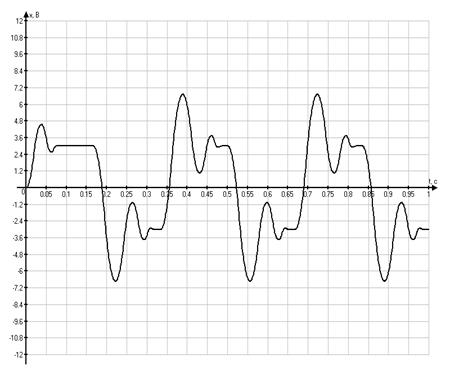
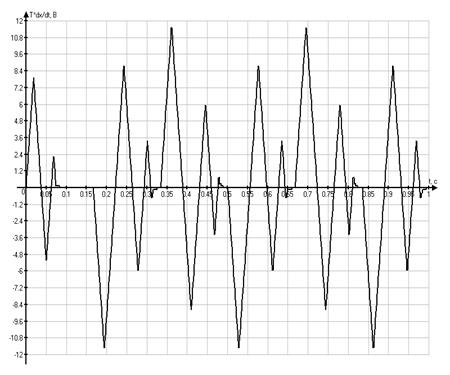
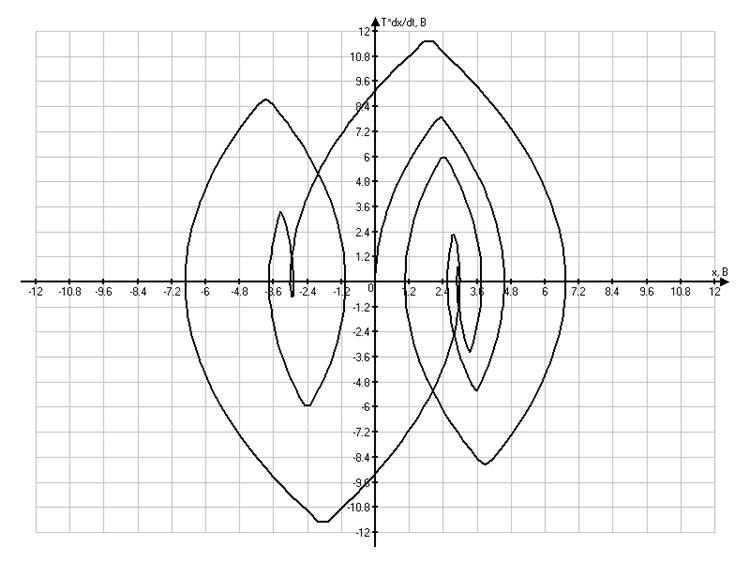
Фазовый портрет в системе координат

3):

Графики временных зависимостей  и , соответственно

 
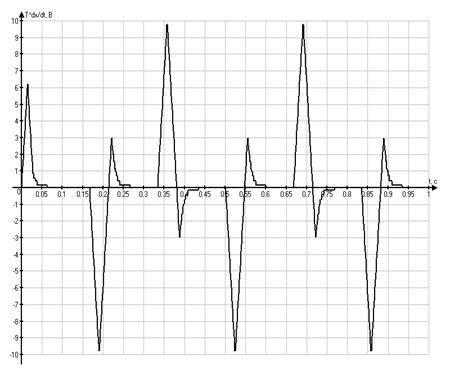
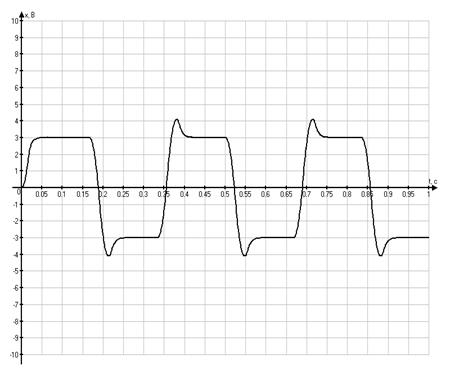
Фазовый портрет в системе координат

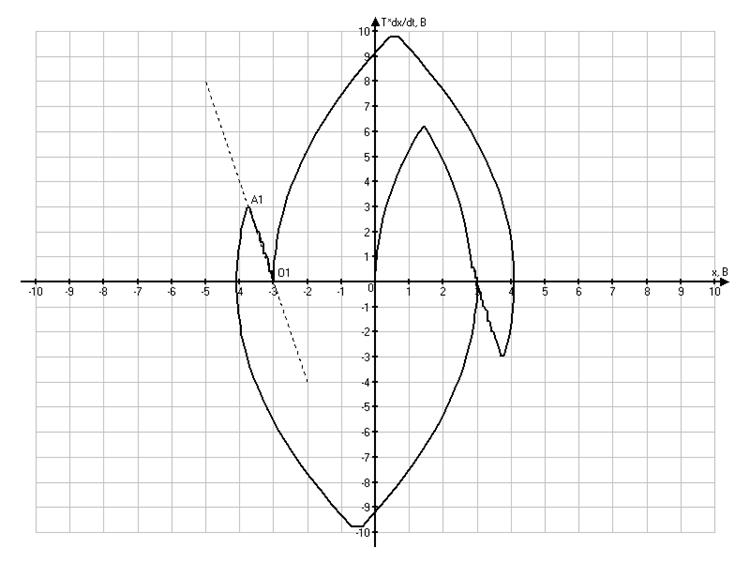
4):

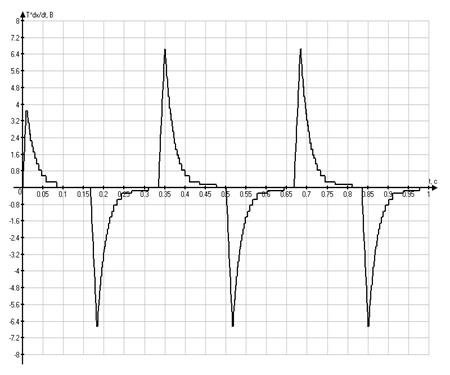
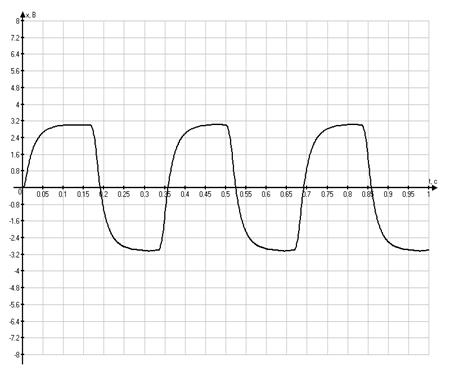
Графики временных зависимостей  и , соответственно

 
Фазовый портрет в системе координат

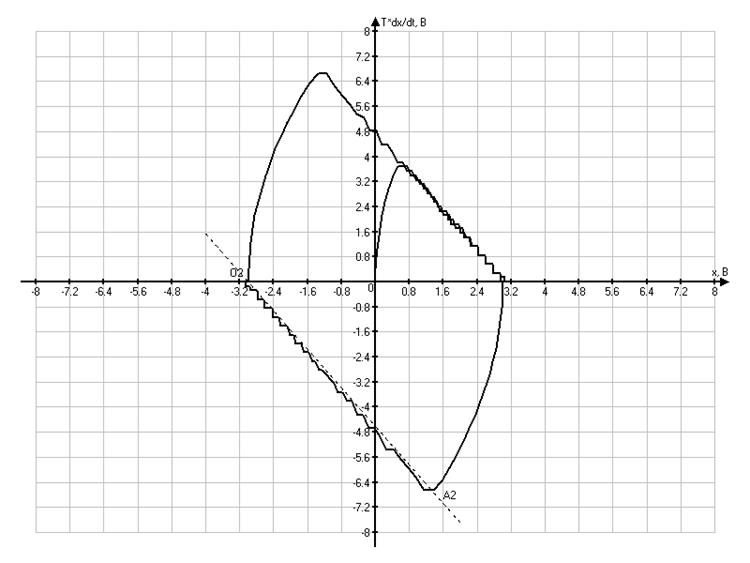
Уже упоминаемые скользящие режимы проявляются при ,. При двух других значениях обратная связь по скорости слишком мала и система переходит в состояние расходящегося колебательного движения, что хорошо видно из осциллограмм.

Рассмотрим третий и четвертый фазовые портреты. Необходимо зафиксировать точки  и . Так как фазовые портреты построены в системе координат , тогда:

           

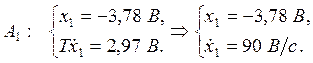
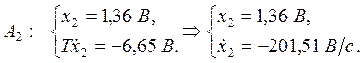
Рассчитаем  для этих случаев:

,

.

Теоретическая часть

Система:

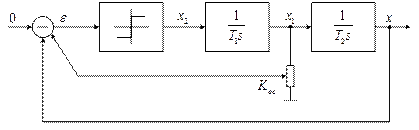
Вышеупомянутую систему можно описать нижеприведёнными уравнениями (будем полагать, что сигнал на входе равен нулю):

, ,                ,

.

Эти уравнения можно представить в виде:

,             .

Дифференциальное уравнение фазовых траекторий:

.

Линия переключения на фазовой плоскости будет описываться уравнением:

.

Справа от этой линии , значит уравнение примет вид:

.

Отсюда:

.

Таким образом, фазовые траектории – это параболы, ветви которых направлены в отрицательную сторону от оси . Положение вершины определяется произвольной постоянной , т.е. начальными условиями переходного процесса , .

Слева от линии переключения наблюдается похожая картина.

Здесь , откуда:

.

Все эти параболы изображены на рисунке, соответственно нашим данным:

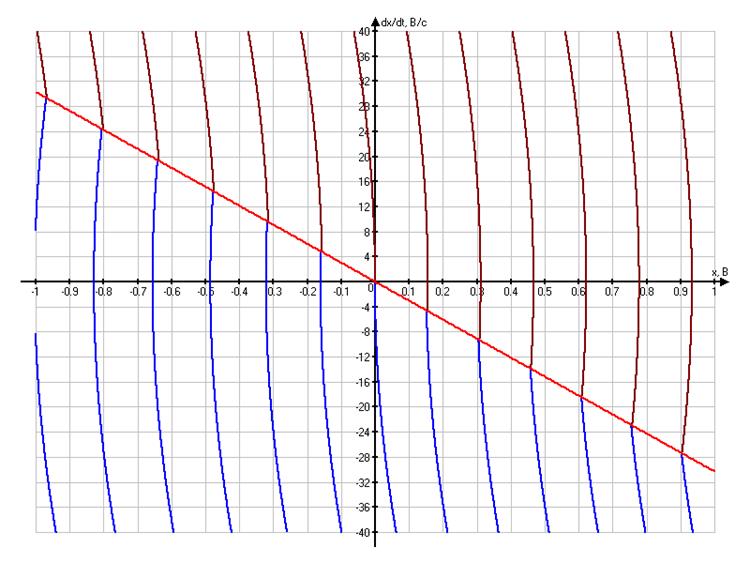
Стоит отметить, что по параболам точка может двигаться только по часовой стрелке. Значит при попадании на одну из линий, точка движется до линии переключения. Как только точка пересечёт линию, она попадёт на другую половину от линии, и её снова устремит к линии, но по траектории более близкой к началу координат и так далее. Таким образом, путём вибраций около линии переключения точка «соскользнёт» к началу координат. В идеале точка двигалась бы строго по линии переключения, это соответствовало бы переключению линейного элемента с бесконечной частотой. Однако, т.к. релейный элемент обладает ограниченным быстродействием, переключение запаздывает, поэтому точка совершает вибрации.

Скользящий процесс характеризуется длиной отрезка , на котором происходит непосредственный вход в скользящий процесс. Найдём его границы.

В точках, определяющих границы этого отрезка, касательные к параболам совпадают с линией переключения. Это условие можно выразить в виде:

, тогда из уравнения фазовых траекторий получим для точек  и , соответственно, условия:

,                   ,

,                      ,

Для наших данных получаем:

,

, или считая для нашей оси :

,       .

Видно, что при полной обратной связи амплитуда соответствует уровню переключения релейного элемента, что и следовало ожидать.

Видим, что отрезок скользящего процесса тем больше, чем больше коэффициент усиления прямой цепи и обратной связи. В нашей работе, мы не меняем значение усиления прямой цепи, влияя только на обратную связь.

Из осциллограмм можно также видеть, что зависимости от времени для  и  определяются простыми переходными процессами первого порядка. Такие процессы весьма желательны для реальных работающих систем.

Данным фактом и объясняется вид фазового портрета в третьем случае. На ней обратная связь меньше настолько, что точка не попадает сразу на отрезок скользящего процесса, а сначала делает дугу по другой параболе, а только потом попадает на этот отрезок. Переходные процессы для  и  имеют уже пики перерегулирования. Такие процессы всё же ещё допустимы для многим реальным систем.

На фазовом портрете во втором случае мы видим, что обратная связь очень мала. При этом отрезок скользящего процесса практически исчезает, и система попадает в расходящийся процесс и «пульсирует» между двумя состояниями, видными на рисунке. Крайний вариант такого процесса, при отсутствии обратной связи по скорости, представлен на первом варианте. Кроме того, переходные процессы имеют сильно выраженный колебательный, а в последнем случае и явно расходящийся вид. Такие процессы недопустимы в реальных системах.