Фазовое пространство и фазовая плоскость нелинейной системы. Фазовое пространство в математике и физике

Фазовое пространство и фазовая плоскость нелинейной системы

Исходные положения

Любая система однозначно характеризуется набором координат, образующих вектор состояния (вектор переменных состояния) системы. Количество линейно-независимых координат (переменных системы) определяет размерность  данного вектора. Такими переменными для системы электропривода могут быть, например, скорость вращения и угол поворота рабочего органа, токи, протекающие по якорным цепям и так далее. В том случае, когда компоненты вектора переменных состояния являются фазовыми переменными, данный вектор называется вектором фазовых переменных.

Фазовое пространство в математике и физике — пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка в этом  пространстве. Фазовое пространство называется в общем случае пространством состояний системы. Размерность этого пространства определяется размерностью вектора состояния (вектора фазовых переменных).      

Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём единственной (изображающей) точкой, а эволюция системы — перемещением этой точки. Кроме того, движение изображающей точки позволяет делать соответствующие заключения о поведении сложных механических систем.

Частным случаем фазового пространства является фазовая плоскость. Фазовая плоскость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка (в физике колебаний по оси абсцисс фазовой плоскости откладывается значения параметра x, а по оси ординат – первая производная x по времени).

Пусть нелинейная система автоматического управления описывается системой дифференциальных уравнений вида

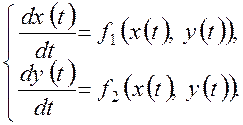
Заданы  начальные условия  и .

Состояние системы в любой момент времени  характеризуется значениями  и .

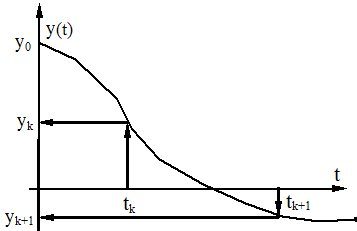
Проведем вышеописанное построение для  . В результате чего получим на плоскости  последовательность точек , ,…, , соединив которые получим графическое изображение кривой .

Точка  называется изображающей точкой.  При изменении  от 0 до  изображающая точка на плоскости  описывает кривую – фазовую траекторию. Плоскость   называется фазовой плоскостью. Через каждую точку фазовой плоскости (как будет показано ниже) проходит лишь одна фазовая траектория (за исключением особых точек). Каждому новому значению начальных условий  будет соответствовать  на фазовой плоскости своя фазовая траектория.

Множество фазовых траекторий на фазовой плоскости  называется фазовым портретом системы автоматического управления. Он даёт представление о совокупности всех возможных сочетаний системы и типах возможных движений в ней.

Значения нелинейных функций  и , стоящих в правой части системы дифференциальных уравнений в каждый момент времени  определяют проекции скорости движения изображающей точки на оси координат  и  соответственно. Это потому, что они, согласно дифференциальным уравнениям, соответственно равны  и .

На фазовой плоскости  существуют характерные особые точки, которые определяются нулевыми значениями проекции вектора скорости: , , или решением системы нелинейных (в общем случае) уравнений:

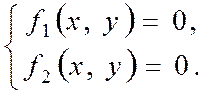
Особые точки соответствуют состоянию равновесия системы. На фазовой плоскости может быть несколько особых точек.

Уравнение фазовой траектории может быть получено и непосредственно из исходной системы дифференциальных уравнений путем исключения дифференциала времени dt: 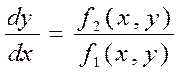     и решается аналитически, например, методом раздедения переменных, или численно, с учетом начальных значений  .

Особенностью фазовых траекторий нелинейных САУ является то, что кроме особых точек на фазовом портрете могут появляться особые траектории. Им соответствуют предельные циклы: устойчивые или неустойчивые. Устойчивый предельный цикл имеет место при наличии в системе автоколебаний. К устойчивым предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям. Размеры предельного цикла характеризуются амплитудами колебаний переменных x и y(выходной величиной x и ее производной 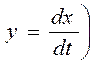. Пересечение траектории устойчивого предельного цикла оси абсцисс