связи с этим различают три ситуации: 1) система устойчива; 2) система неустойчива; 3) система "безразличная", нейтральная.
Оценить устойчивость системы можно в результате исследования ее математической модели, то есть решить соответствующую систему дифференциальных уравнений.
Для разомкнутой системы математическая модель в операторной форме:
![]() , или
, или 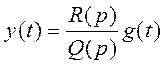 , где
, где ![]() - оператор
дифференцирования.
- оператор
дифференцирования.
Для замкнутой системы:
![]() , или
, или 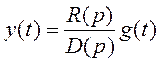 . Если
. Если ![]() (единичная обратная
связь), то
(единичная обратная
связь), то ![]() .
.
С учетом
введенного понятия устойчивости для ее анализа необходимо рассматривать только
собственное движение системы, определяемое однородным дифференциальным
уравнением ![]() или
или ![]() .
.
Рассмотрим
замкнутую систему. Если подать на ее вход импульсное воздействие ![]() , то реакция системы на
данный сигнал (весовая функция системы):
, то реакция системы на
данный сигнал (весовая функция системы): 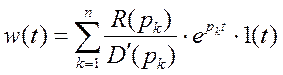 . n
- порядок системы (старшая степень полинома D(p)).
. n
- порядок системы (старшая степень полинома D(p)).
Рассмотрим составляющую весовой функции, обусловленную i-м корнем:
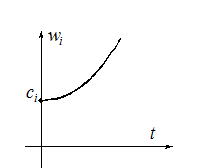
![]() .
.
Пусть ![]() (вещественный корень).
(вещественный корень).
Если ![]() , тогда
, тогда ![]()
возрастает, смотри рисунок:
То есть, если хотя бы одно звено "расходящееся", то вся система - неустойчива.
Если ![]() , тогда
, тогда ![]() , как следует из рисунка,
асимптотически убывает:
, как следует из рисунка,
асимптотически убывает:
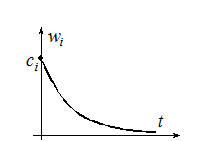
Если все корни
характеристического уравнения ![]() вещественные
отрицательные:
вещественные
отрицательные: ![]() ,
то система устойчива.
,
то система устойчива.
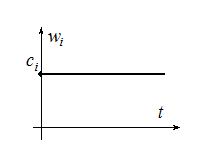 Если хотя бы один
Если хотя бы один ![]()
при всех остальных отрицательных
![]() , то система -
"безразличная":
, то система -
"безразличная":
В случае пары
комплексных корней, ![]() ,
, ![]() , соответствующие
составляющие весовой функции имеют вид:
, соответствующие
составляющие весовой функции имеют вид:
![]()
![]()
![]()
Если
вещественная часть комплексных корней отрицательна (![]() ),то система
устойчива.
),то система
устойчива.
Если ![]() - система неустойчива.
- система неустойчива.
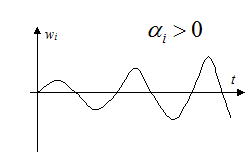
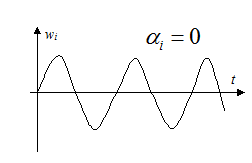
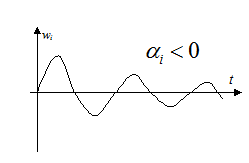 Если
Если ![]() (чисто мнимые корни)
при всех остальных "устойчивых" корнях система
"безразличная".
(чисто мнимые корни)
при всех остальных "устойчивых" корнях система
"безразличная".
Если все вещественные корни и вещественные части всех комплексных корней характеристического уравнения системы отрицательны, тогда система - устойчива. Весовая функция такой системы есть убывающая к нулю зависимость. Физически это означает, что по окончании импульсного внешнего воздействия устойчивая система возвращается в первоначальное состояние.
Распространение устойчивости на линеаризованные системы. 1892г. Ляпунов А.М.
1. Для устойчивости линеаризованных систем необходимо и достаточно, чтобы все корни характеристического уравнения математической модели системы (полюса) были либо отрицательными вещественными, либо имели отрицательные вещественные части. При этом никакие отброшенные при линеаризации члены высших порядков не сделают систему неустойчивой.
2. Если в линеаризованный системе хотя бы один корень характеристического уравнения будет положительным вещественным, либо иметь положительную вещественную часть, то система будет неустойчива, и никакие отброшенные члены высших порядков не сделают ее устойчивой.
3. Если один или пара корней характеристического уравнения системы находятся на мнимой оси, а остальные корни все левые, то система находится на границе устойчивости. Ее реальная устойчивость целиком определяется отброшенными при линеаризации малыми высших порядков.
Поскольку для установления факта устойчивости системы необходимо знать только знак вещественной части корня, то желательно иметь какие-то критерии, которые бы позволяли определять этот знак без нахождения корней характеристического уравнения, тем более без процедуры решения дифференциального уравнения, соответствующего математической модели исследуемой системе.
Различают алгебраические и частотные критерии.
Алгебраические: критерий Рауса; критерий Гурвица;
критерий Вышнеградского;
Частотные: критерий Эрмита-Михайлова;
критерий Найквиста;
Раус выразил его в
форме таблицы. Элементами первой строки являются четные коэффициенты
характеристического уравнения (полинома), начиная с ![]() .
Элементы второй - нечетные коэффициенты, начиная с
.
Элементы второй - нечетные коэффициенты, начиная с ![]() .
Элементы последующих строк вычисляются по приведенным формулам.
.
Элементы последующих строк вычисляются по приведенным формулам.
Итак, характеристический
полином ![]() , где
, где ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и так далее |
… |
… |
… |
В данной таблице должна быть n+1 строка.
Ниже приведены формулы, используемые при заполнении таблицы.
![]() ;
; ![]() ;
;
![]()
![]() ;
;
Если все элементы первого столбца таблицы Рауса положительны (одного знака), то система устойчива. Если хотя бы один элемент отрицателен, то система неустойчива. При этом число перемен знака равно числу правых корней характеристического уравнения.
Если один из элементов первого столбца равен нулю, то система находится на границе устойчивости, а характеристическое уравнение имеет пару мнимых корней.
В случае, когда последний элемент равен нулю, то корень уравнения – нулевой вещественный. При нескольких нулевых последних элементах первого столбца таблицы имеется соответствующее количество нулевых корней характеристического уравнения.
На основании характеристического уравнения системы
![]()
![]() .
.
строится определитель Гурвица (при ![]() ).
).
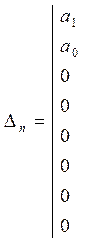
![]()
![]()
![]()
![]()
![]()
![]()
![]() Свободные места заполняются
нулями.
Свободные места заполняются
нулями.
Для устойчивости системы необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительны.
Диагональные миноры:
![]() ;
; 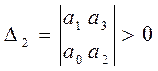 ;
; 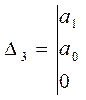
![]()
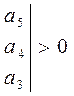 ; . . .
; . . .
Пример 1. Пусть имеется система
первого порядка, ![]() .
.
![]() ; (или
; (или ![]() ;
; ![]() );
); ![]()
![]() .
.
![]() - не абсолютная величина, а
определитель!!!
- не абсолютная величина, а
определитель!!!
Вывод. Для устойчивости системы первого порядка необходима положительность коэффициентов характеристического уравнения.
Здесь и ниже использовано свойство идентичности операторных форм
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.