Проблема устойчивости моделей нелинейных ДСАУ. Модернизация кругового критерия абсолютной устойчивости нелинейных систем В. А. Якубовича

Современные проблемы автоматизации и управления

Лекции проф. для магистров

Лекции 8 (06. 11),  оригинал 05. 11. 2009г

Содержание предыдущей лекции. Кратко описаны основные физические структуры дискретных систем, приводящие к использованию нелинейных моделей при их описании. Особо часто встречается модель ДСАУ с широтно-импульсной модуляцией первого рода (ШИМ - I). Кратко изложены принципы эквивалентности  ШИМ - АИМ. Это позволяет принять модуляцию  линейной в нелинейной ДСАУ (НДСАУ). Для этого случая применим описанный  критерий устойчивости НДСАУ Якова Цыпкина (Москва). Подробно описаны типовые структуры НДСАУ с линейными и нелинейными видами модуляции. Сделан важный вывод о том, что для моделей ДСАУ с нелинейными видами модуляции следует использовать иные критерии устойчивости. Описан один из них А. Х. Гелига. (СП б)

ГЛАВА 4. Проблема устойчивости моделей нелинейных ДСАУ

(продолжение)

5. 4 Модернизация кругового критерия абсолютной устойчивости нелинейных систем В. А. Якубовича

Уважаемые студенты! В изложенной вам теории аналоговых нелинейных систем (7 семестр) описан  "круговой" критерий абсолютной устойчивости нелинейных систем, разработанный петербургским ученым Владимиром Андреевичем Якубовичем (СПб - ГУ) (1962г.). Однако этот критерий в применении к моделям дискретных САУ нуждается в уточнениях. Кроме того, Вы только что познакомились с критерием абсолютной устойчивости моделей НДСАУ А. Х. Гелига. Зачем Вам изучать иные критерии?!!

Напомню, что критерий Гелига пригоден для исследования моделей систем, где обрабатываются  однополярные импульсы ШИП, а таких преобразователей (усилителей мощности) практически используют не так уж много. Линейная часть исследуемых моделей систем ограничена узким набором статически устойчивых структур.

Кроме того, малодоказаны (хотя бы для меня С.К.) неравенства (7. 7) и (8. 7), составляющие теоретическую основу критерия. Поэтому познакомимся с возможностями решения той же проблемы круговым критерием абсолютной устойчивости, (который все ещё находится в наших, совместных  с Вами, уточнениях и доработках) (С. К.).

Будем рассматривать модель двухполярного  широтно-импульсного преобразователя (ШИП), который чаще используется в качестве усилителя мощности, чем однополярный преобразователь. Для кругового критерия абсолютной устойчивости В. Якубовича модель такого ШИП нужно отнести к нелинейностям классов "0 - к" или "к₁ - к₂".

Обобщенную структуру такой модели мы изобразили на рис.2. 7 (см лекцию 7). Эпюру напряжения выхода двухполярногоШИП представим  на рис.1.8

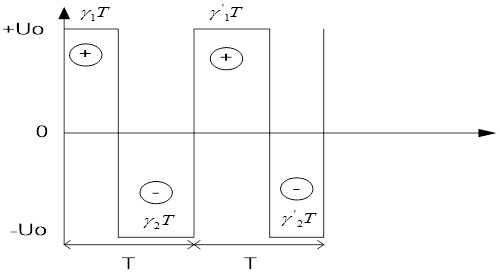
Рис. 1.8. Эпюра напряжения выхода двухполярного широтно - импульного преобразователя (ШИП)

Если положить продолжительность положительного импульса напряжения , то среднее его значение будет U_ср.= U₀ T/T(γ₁-γ₂)<0, и наоборот.

Поскольку , то , где  относительная продолжительность импульса. Тогда коэффициент крутизны двухполярного ШИП σ можно вычислить по таким же коэффициентам χ₁ и χ₂, как для однополярного ШИП по формуле:

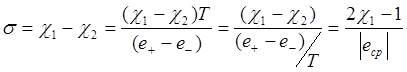.                             (1. 8)

Важное замечание. Коэффициенты крутизны χ и σ  играют очень важную роль в "поведении" ШИП. Для однополярного ШИП его внешняя характеристика U_ср.= U₀ γ=f (e_вх) четносимметрична, а реальный диапазон изменения  среднего напряжения составляет:

"Лучшие" величины γ современными электронными средствами не создать. Значит и диапазон "d" бòльший не получить.

Для двухполярного ШИП его внешняя характеристика с_р.= U₀ σ =f (e_вх) нечетно - симметрична, а реальный диапазон изменения  среднего напряжения составляет:

О лучшем диапазоне для усилителя мощности "нельзя и мечтать"! Всё это и имелось в виду в начальной части лекции.

Итак, нечетно - симметричную статическую характеристику двухполярного ШИП, необходимую для кругового критерия абсолютной устойчивости НДСАУ, мы получили.

Теперь найдем дискретную передаточную функцию (ДПФ) усилителя мощности (ШИП) и линейной части (ЛЧ) НДСАУ. С помощью рис.1. 8 можно представить модель ШИП как "экстраполятора нулевого порядка с запоминанием на неполный интервал γΤ" (с амплитудой ) из которой вычитается модель обычного экстраполятора нулевого порядка (с амплитудой U₀) Для ЛЧ имеем передаточную функцию (ПФ)  Проделаем эти преобразования:

,

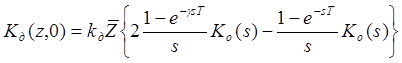или, после несложных преобразований получим:

      (2. 8)

где  - коэффициент передачи двухполярного ШИП,

- несмещенное z- преобразование ЛЧ,

, смещенное z- преобразование ЛЧ.

Воспользуемся теперь первой гипотезой М. Айзермана (рис. 2. 8) и будем полагать, что статическая нелинейность двухполярного ШИП расположена в угле, образованном двумя прямыми и .

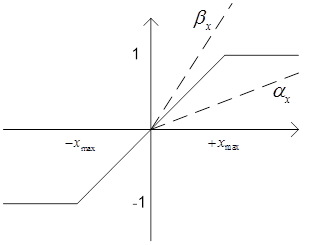
Рис.2. 8 Характеристики коэффициентов передачи к₁ и к₂ линейных систем с той же ЛЧ, что и нелинейная система со статической нелинейностью σ (иллюстрация)

к первой гипотезе М. Айзермана.

Суть первой гипотезе Айзермана: если внутри угла образованного характеристиками двух  статических линейных систем с одинаковой линейной частью ЛЧ и разными коэффициентами передачи к₁ и к₂ (устойчивыми в замкнутом состоянии) расположена статическая нелинейность, то нелинейная система, с той же ЛЧ будет устойчива

Эта гипотеза позволяет нам выбрать значения к₁ и к₂, а  формула (2. 8) рассчитать АФХ НДСАУ, необходимую для кругового критерия абсолютной устойчивости. Ниже приведены примеры использования  кругового критерия.

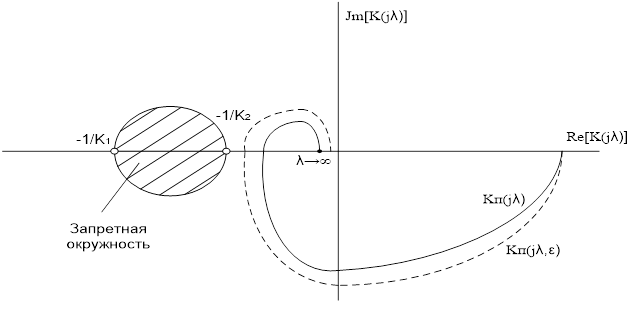
Рис.3. 8. Пример использования кругового критерия для исследования абсолютной устойчивости модели НДСАУ при k₁>0 и k₂>0.

Характеристики , построенные на рис.3. 8. по формуле (2. 8), должны охватывать изменение смещения ε от "0" до"1". Обычно берут ε=0,1, 0,25, 0,5, 0,75, 0,9.(симметрично различающиеся АФХ). Все такие характеристика не должна заходить в запретную окружность. Линейная часть системы должна быть устойчива (как и при критерии А. Гелига).

Но специфика формулы (2.8) состоит в том, что при γ₁ =0,5 коэффициент σ=0 и среднее значение напряжения двухполярного ШИП равно нулю. Поэтому АФХ линейной части модели НДСАУ при этих условиях построить невозможно. Следовательно, достаточно вычислить и построить одну АФХ при γ₁ =1,0.

Другой случай расположения нелинейности изображен на рис.4. 8.

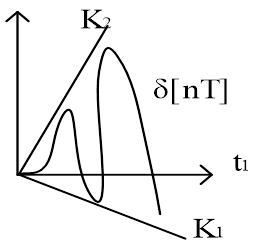
Рис.4. 8 Нелинейность расположена в угле к₂>0, а к₁<0

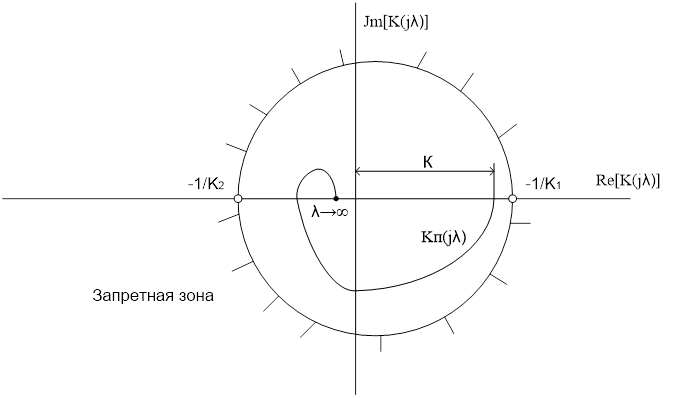
Рис5. 8.Расположение амплитудо - фазных характеристик ЛЧ нелинейной дискретной системы.

Тогда запретная область (рис. 5. 8) будет вне круга, а разрешенная только внутри его, а это, в свою очередь, может означать сильное ограничение коэффициента передачи ЛЧ.

Можно построить другие K₂ и K₁ для неустойчивых или нейтральных (астатических) линейных частей. В этом заключается существенное преимущество кругового критерия абсолютной устойчивости, по сравнению с описанным выше критерием А. Гелига. Но мы  не будем эти вопросы развивать в этой лекции, так - как они были подробно рассмотрены нами на четвертом курсе при изучении "Теории управления нелинейными системами" (см. папку Lk.NSAU.09, файл Лек. 9НСАУ,1.doc) и в литературе [10].

Оформила:     Беляева Н.И.  05.11.2009. Скорректировано 05.12, 20.12.2010 и 06.01.2011.