Погрешности преобразования информации в дискретных системах автоматического управления (ДСАУ). Методы дискретного интегрирования и устойчивость их алгоритмов

Современные проблемы автоматизации и управления

Лекции проф. для магистров

Лекция 3.(записано: 18.09.2009)

 Содержание предыдущей лекции. Завершено изложение материалов по сравнению частотных спектров аналоговых и дискретных функций, основанному на преобразовании Лайнвиля. Закончено решение примеров использования этого преобразования. Пояснена оригинальная методика решения таких задач.

Глава 1. Погрешности преобразования информации в дискретных системах автоматического управления (ДСАУ)(продолжение)

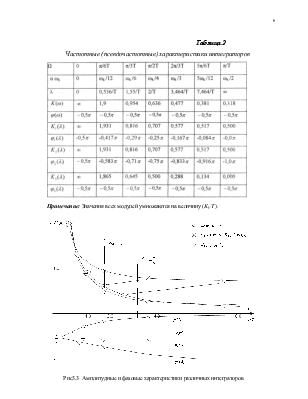
1.5. Методы дискретного интегрирования и устойчивость их алгоритмов

В дискретных системах применяется три метода интегрирования дискретных функций, которые заложены в конкретные программы обработки информации, поэтому очень полезно знать свойства каждого метода интегрирования. На рис.1. 3.изображены эпюры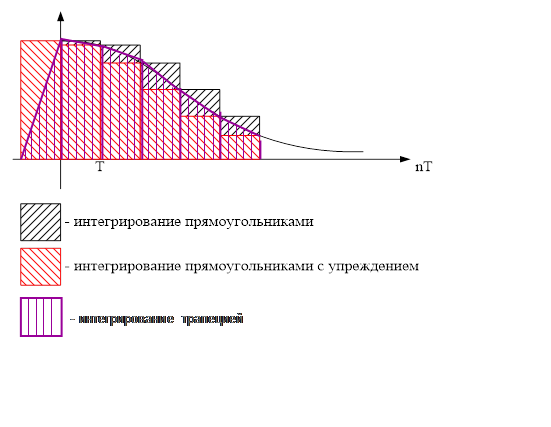 и приведены русские названия всех методов интегрирования¹⁾.

Рис.1. 3. Эпюры дискретных функций интегрирования непрерывной огибающей y_T(nT)

плюс прямоугольники заштрихован ные красным цветом

________________________________________________________________________________

1)  Стыдно, но приходится еще раз признать, что наши "профессионально - технические" термины подчас не только неточны, но и неверны исторически. Это связано с тем, что они часто приходят в Россию из переводной иноязычной технической литературы и закрепляются на новой языковой базе. Вот и в данном случае, если обратиться к "Вычислительной математике", то там давно известно множество методов "численного интегрирования" (в том числе и изучаемые в этой лекции). Только там их называют "грамотнее": Метод (интегрирования) прямоугольниками - Метод (интегрирования) Эйлера; - прямоугольниками с упреждением - Метод - Эйлера в реальном масштабе времени; - трапециями  - Метод  Эйлера улучшенный. Еще часто используются программы интегрирования  Рунге - Кутта 3го порядка; Рунге - Кутта - 4 - го порядка и др. Так что программы интегрирования весьма разнообразны.

Кроме того напомним, что в аналоговых устройствах введение интеграторов ухудшает условия устойчивости замкнутой системы за счет возрастания фазового сдвига управляемого сигнала на (-90⁰) от каждого интегратора. Что же происходит при "дискретном " интегрировании?

1.  Интегрирование" прямоугольниками".

В иностранной литературе и в различных средах разработки/ моделирования метод называется «backward Euler», «backward Rectangular»,"интегрирование правыми прямоугольниками". В России название метода указано в заголовке. Его алгоритм выглядит следующим образом:

                                                 (1.3)

Обычно данный метод используется везде "по умолчанию".

Дискретная передаточная функция (ДПФ) интегратора, реализованного этим методом, выглядит следующим образом:

                                                               (2.3)

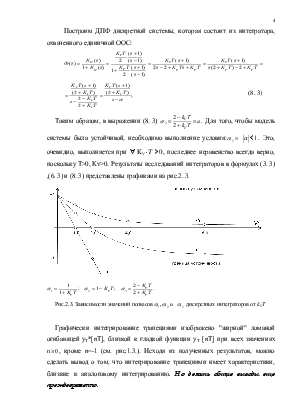
Построим ДПФ дискретной системы, которая состоит из интегратора, охваченного отрицательной единичной обратной связью (ООС). (В аналоговом виде мы бы получили апериодическое звено):

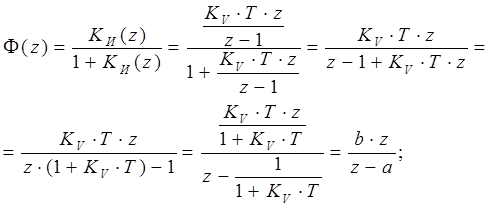                             (3. 3)

Для того чтобы модель система была устойчивой, необходимо выполнение условия: . Это, очевидно, выполняется при . Последнее неравенство так же всегда верно, так - как T>0, K_V>0.

Исходя из полученных результатов, можно сделать вывод о том, что данный метод интегрирования не снижает запас устойчивости ДСАУ.

2. "Интегрирование прямоугольниками с упреждением".

В иностранной литературе и в различных средах разработки/ моделирования метод называется «forward Euler», «forward Rectangular» В  русскоязычной его называют «интегрирование прямоугольниками с упреждением». Его алгоритм представим в таком виде:

                                             (4. 3)

Дискретная передаточная функция (ДПФ) интегратора, реализованного таким образом, будет:

                                                                          (5. 3)

Построим ДПФ дискретной системы, которая состоит из интегратора, охваченного единичной ООС. (В аналоговом виде мы бы получили бы апериодическое звено):

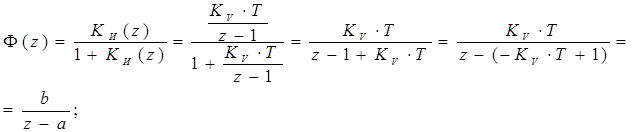               (6. 3)

где, .

Для того, чтобы система была устойчивой, необходимо выполнение условия: . Это, очевидно, выполняется при 0<k_VT<2. Исходя из полученных результатов, можно сделать вывод о том, что данный метод интегрирования дает худший результат, в смысле устойчивости САУ, по сравнению с методом

«прямоугольников». Здесь необходимо, при заданном значении добротности k_V, правильно выбирать шаг квантования T.

3. Преобразование Тастина (Tusten) (Интегрирование трапециями)

Дискретная передаточная функция (ДПФ) интегратора, реализованного данным методом, выглядит следующим образом:

                                                                       (7. 3)