Построим ДПФ дискретной системы, которая состоит из интегратора, охваченного единичной ООС:
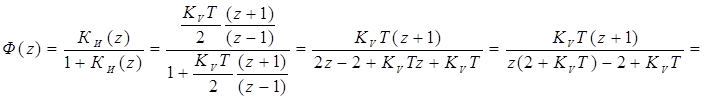
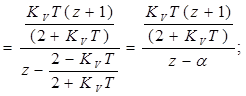 (8. 3)
(8. 3)
Таким образом, в выражении (8. 3) ![]() . Для того, чтобы модель системы
была устойчивой, необходимо выполнение условия:
. Для того, чтобы модель системы
была устойчивой, необходимо выполнение условия:![]()
![]() . Это, очевидно, выполняется при
. Это, очевидно, выполняется при ![]() , последнее неравенство всегда
верно, поскольку T>0, Kv>0. Результаты исследований интеграторов в
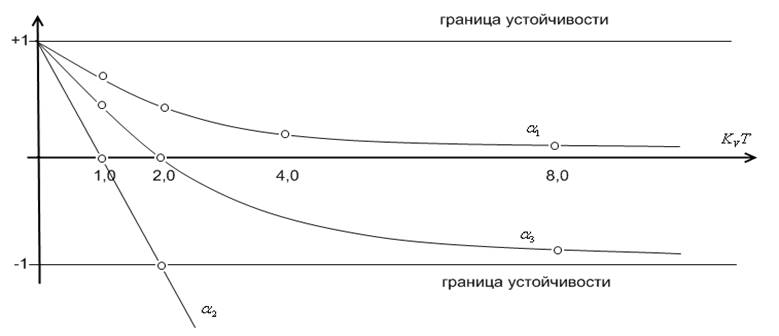
формулах (3. 3) ,(6. 3) и (8. 3) представлены графиками на рис.2. 3.
, последнее неравенство всегда
верно, поскольку T>0, Kv>0. Результаты исследований интеграторов в
формулах (3. 3) ,(6. 3) и (8. 3) представлены графиками на рис.2. 3.
![]()
Рис.2.3. Зависимости значений
полюсов ![]() дискретных интеграторов от kVT
дискретных интеграторов от kVT
Графически интегрирование
трапециями изображено "жирной" ломаной огибающей yT*[nT],
близкой к гладкой функции yT [nT] при всех значениях n![]() , кроме n=-1 (см. рис.1.3.). Исходя
из полученных результатов, можно сделать вывод о том, что интегрирование
трапециями имеет характеристики, близкие к аналоговому интегрированию. Но
делать общие выводы еще преждевременно.
, кроме n=-1 (см. рис.1.3.). Исходя
из полученных результатов, можно сделать вывод о том, что интегрирование
трапециями имеет характеристики, близкие к аналоговому интегрированию. Но
делать общие выводы еще преждевременно.
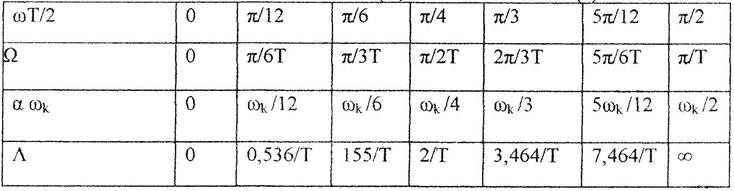
Поэтому вычислим и сопоставим (частотные) псевдочастотные амплитудные и фазовые характеристики всех трех дискретных и аналогового интегратора. Для этого составим вначале вспомогательную табл.1
Таблица 1
Соотношение обычной частоты (ω) и псевдочастоты (λ):
Теперь вычислим передаточные функции и частотные характеристики интеграторов:
- аналоговый интегратор:
![]() .
.
![]()
- дискретное интегрирование прямоугольниками:
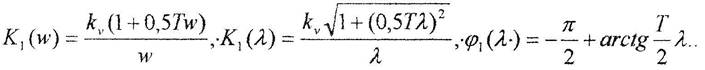
- дискретное интегрирование прямоугольниками с упреждением:
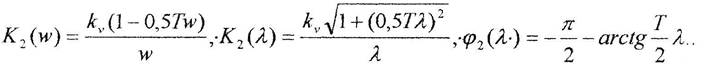
- дискретное интегрирование трапециями:
![]()
В табл.2 представим данные расчета характеристик всех интеграторов по вышеприведенным формулам.
Таблица 2
Частотные (псевдочастотные) характеристики интеграторов
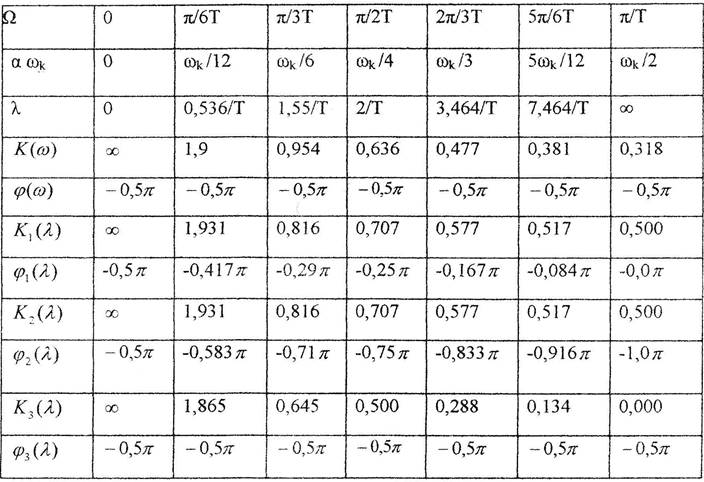
Примечание: Значения всех модулей умножаются на величину![]() .
.
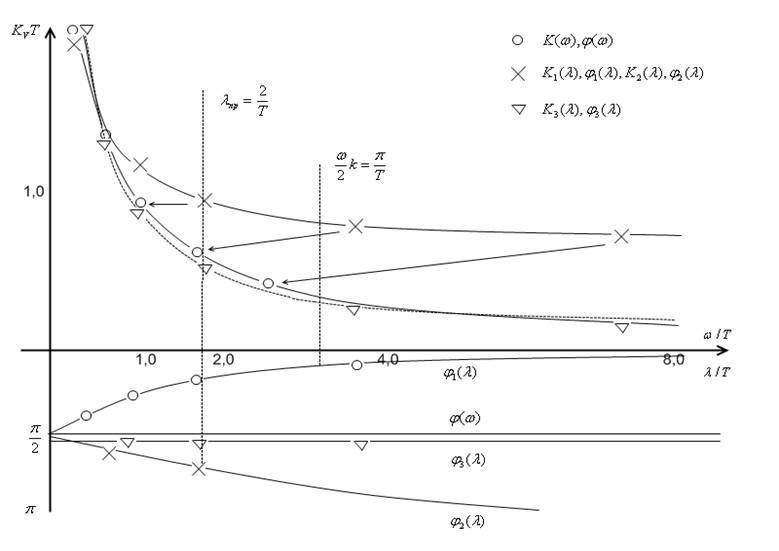
Рис3.3 Амплитудные и фазовые характеристики различных интеграторов
На основании всех исследований можно сделать такие выводы.
1. Алгоритм дискретного интегрирования прямоугольниками метод Эйлера можно признать наиболее рациональным так - как он имеет хорошее воспроизведение амплитуд и существенно уменьшающуюся отрицательную фазу управляемого сигнала по отношению к управляющему сигналу Последнее свойство может обеспечить больший запас устойчивости модели ДСАУ по сравнению с аналоговой САУ при равных параметрах моделей систем. Алгоритм управления дискретным интегратором устойчив при любых значениях параметров.
2. Метод интегрирования прямоугольниками с упреждением имеет ограниченно устойчивый алгоритм управления. Наиболее плохо, что фазовый сдвиг этого интегратора более (-900) и возрастает по мере роста частоты до(-1800) . Это существенно ухудшает условия устойчивости модели ДСАУ по сравнению с аналоговой САУ.
3. Метод интегрирования трапециями (Преобразование Тастина)улучшенный метод Эйлера имеет частотные характеристики такие же, как аналоговый интегратор, и его полезно применять в цифровых системах, предназначенных для замены аналоговых регуляторов, в таких случаях, когда по технологическим или иным причинам нельзя изменять динамические режимы автоматизированных агрегатов при модернизации их систем управления.
Существенное примечание (не по теме лекции). Преобразование Тастина получаем, как полу сумму интегрирования левыми и правыми прямоугольниками, а именно:
![]() .
(9. 3)
.
(9. 3)
При добротности по скорости kV=1 имеем:
![]() .
(10.3)
.
(10.3)
Собственно выражение (10. 3) и называют "преобразованием Тастина".
Многие специалисты полагают, что с помощью "преобразования Тастина" наиболее просто перейти от передаточных функций (ПФ) аналоговых моделей к ДПФ цифровых моделей и далее выполнять исследование их поведения в "Z" или "w" комплекснозначых плоскостях (см., например, очень интересную работу [27]).
Пример. Выполнятся
проект с программной реализацией цифрового корректирующего устройства для
непрерывного объекта с ПФ вида: ![]() . Требуется получить
ДПФ модели цифровой САУ и выполнить ее аналитическое исследование. Для модели
объекта, применяя преобразование Тастина, получим ДПФ в таком виде.
. Требуется получить
ДПФ модели цифровой САУ и выполнить ее аналитическое исследование. Для модели
объекта, применяя преобразование Тастина, получим ДПФ в таком виде.
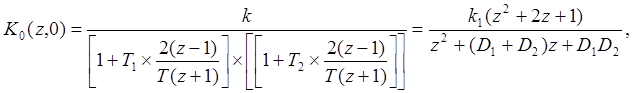 (11. 3)
(11. 3)
где ![]()
![]() , T
величина интервала квантования.
, T
величина интервала квантования.
Если найти ДПФ объекта по "стандартным" "Z" преобразованиям , то вместо выражения (11. 3) получим:
![]() , (12.
3)
, (12.
3)
где
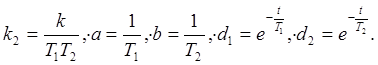
Соответствие выражений (11. 3) и (12. 3) я (С.К) не обсуждаю, поскольку свое мнение по поводу бесполезности "преобразования Тастина" высказал в курсе "Теория ДСАУ".
Оформил: Мокринский Д.О.01.10.2009.
Скорректировал: Савельев И.С. 08.10.2010.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.