Выбор двигателя. Типоразмер двигателя. Динамическое исследование машинного агрегата. Приведённый момент инерции

Факультет Технической Кибернетики

Кафедра «Систем автоматического управления»

Пояснительная записка ПЗ08.24.04.1986

к курсовому проекту по механике

Выполнил:

группа: 3083/2

Преподаватель:

2009 г.

1. Выбор двигателя:

Используя формулу 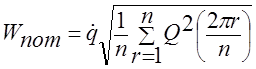 ,высчитаем величину потребляемой мощности двигателя: W_пот=10996Вт, где

С помощью каталога выберем двигатель:

Типоразмер двигателя	Мощность	Скорость	Номинальный ток , Iн	Номинальное напряжение, u н	Сопротив-	Индуктивность	Момент инерции ротора, Jр
	Nдн	nдн			ление, R	L
	Вт	об/мин	А	В	Ом	Гн	кгм2
2ПН112L	2 200	1 500	11	220	0,968	0,014	0,018

Двигатель 2ПН112L удовлетворяет всем условиям:

1) W_дн=2200Вт≥ W_пот=996Вт

2) неравенство: . Верно (440 кгм >183,3кгм)

Использовались формулы 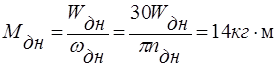 и , где g - коэффициент перегрузки задан равным 2.

Параметры этого двигателя:

а) число оборотов в минуту на холостом ходу

б) электромагнитную постоянную времени

в) крутизну статической характеристики двигателя .

Передаточное число редуктора:

2. Динамическое исследование машинного агрегата:

«Задачей динамического исследования машины является определение закона движения входного звена исполнительного механизма  с учетом динамических свойств приводного двигателя, движущего момента  и динамической нагрузки в приводе , а также оценка неравномерности вращения входного звена и проверка перекладки зазоров в приводе, улучшение динамических показателей качества машины»

Машинный агрегат состоит из двигателя, передаточного и исполнительного механизмов. Динамический расчет машинного агрегата связано с определением и исследованием стационарного решения системы дифференциальных уравнений

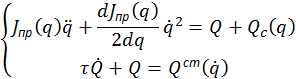
Первое уравнение системы представляет собой уравнение механической системы агрегата, рассматриваемой как механизм с жесткими звеньями, обладающими одной степенью свободы (подвижности). В этом уравнении  - обобщенная координата; - приведенный момент инерции механической системы; - приведенный момент сил сопротивления.

Второе уравнение системы является приведенной динамической характеристикой двигателя. Здесь  - постоянная времени двигателя;  - приведенная статическая характеристика двигателя, разрешенная относительно момента.

Первым этапом динамического исследования машинного агрегата является определение коэффициентов, входящих в систему дифференциальных уравнений:

а) Приведённый момент инерции определяется по формуле                           

, где - переменная часть приведённого момента инерции, -момент инерции двигателя, которые вычисляется по формулам:

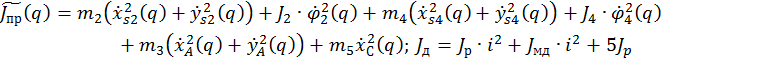
Полученную функцию  с целью упрощения динамических расчетов разложить в ряд Фурье с точностью до пяти гармоник:, где  без маховика

Коэффициенты ряда Фурье для приведённого момента инерции:

Построим графики функции переменной части приведённого момента инерции(Ĵ_пр) и её разложения в ряд Фурье(Ĵ_пр^*) для 12^и точек:

q	Ĵпр	Ĵпр*
0	-0,0612	-0,0599
30	-0,0278	-0,029
60	0,0024	0,0035
90	0,0143	0,0132
120	0,004	0,0052
150	-0,0258	-0,027
180	-0,0607	-0,0594
210	-0,0557	-0,0573
240	0,0557	0,0576
270	0,1604	0,1582
300	0,0509	0,0529
330	-0,0565	-0,0581
360	-0,0612	-0,0599

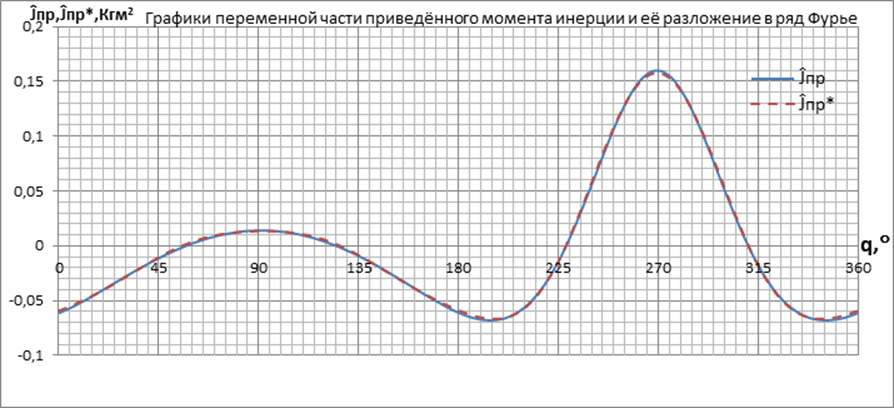
Производная от приведенного момента инерции по обобщенной координате вычисляется по формуле: .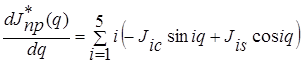

Её график для 12^и точек:

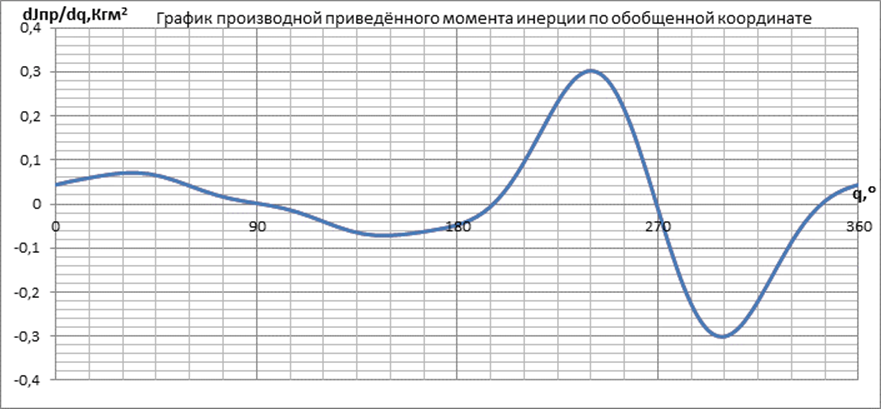
б) Приведенный момент сил сопротивления определяется по формуле:

 , где 

Функция  раскладывается в ряд Фурье с точностью до пяти гармоник:

Коэффициенты ряда Фурье для приведённого момента сил сопротивления:

Построим графики функции переменной части приведённого момента сил сопротивления(Õ_с) и её разложения в ряд Фурье(Õ_с^*) для 12^и точек:

q	Õc	Õc*
0	-32,5198	-32,3279
30	-77,534	-77,7051
60	-102,308	-102,1493
90	-110	-110,1525
120	-101,836	-101,6841
150	-76,7772	-76,9336
180	-30,2541	-30,0849
210	43,8337	43,6397
240	135,5808	135,8128
270	183,3333	183,0698
300	130,1772	130,4335
330	38,3046	38,0818
360	-32,5198	-32,3279

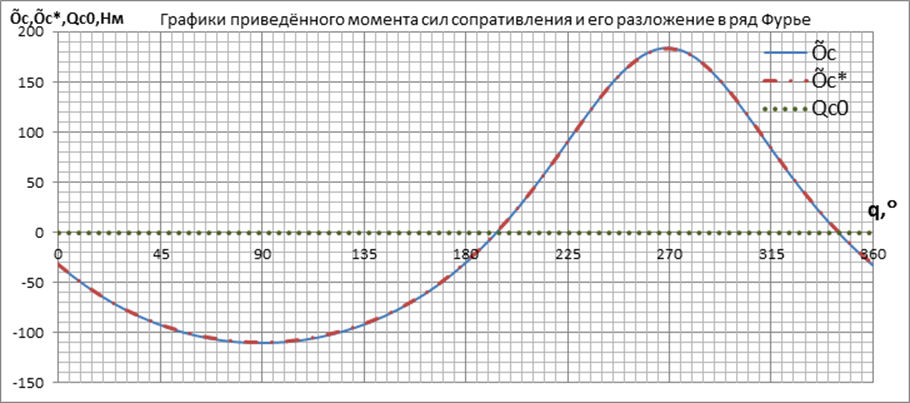
в) Определим приведенную статическую характеристику двигателя: где  - угловая скорость холостого хода ротора двигателя.

3. Решение уравнений движения машины:

Система дифференциальных уравнений движения (см.п.2) содержит две неизвестные функции времени  и . Для отыскания стационарного решения этих уравнений воспользуемся методом последовательных приближений. Для этого уравнения запишем в такой форме, чтобы в правых частях стояли только те слагаемые, которые явно содержат , поскольку они вызывают отклонения закона движения от программного (равномерного) вращения:

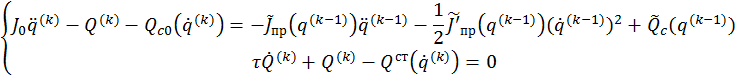
где волнистой линией обозначены переменные части соответствующих функций.

В нулевом приближении, т.е. при  получаем систему уравнений

Пусть

Известно, что , а  

Тогда решение этой системы:

 

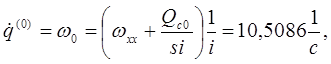
При установленном тормозе, с моментом Qt=180Нм:

 

При  получим систему уравнений

Выражение, стоящее в правой части  первого уравнения – возмущающий момент: характеризует внутреннюю виброактивность исполнительного механизма.

Решение системы уравнений в первом приближении ( разыскиваем в виде  

Здесь  - отклонение закона движения входного звена от программного (равномерного) движения, называемое динамической ошибкой по углу;  - отклонение движущего момента от среднего значения. Подставив эти решения в систему уравнений, получим

Разложим возмущающий момент на программном движении  в ряд Фурье с точностью до пяти гармоник:  где ;

L₁=136,46;L₂=34,3;L₃=10,51;L₄=3,6;L₅=1,36;

Построим график возмущающего момента для 12 точек:

w0t	L* без тормоза	L* с тормозом
0	-34,7422	-34,5548
30	-81,5967	-81,2946
60	-104,4439	-104,2658
90	-110,2599	-110,2516
120	-99,5017	-99,6711
150	-72,9946	-73,3004
180	-27,4575	-27,6615
210	38,4535	38,8561
240	119,1166	120,4127
270	183,5101	183,4759
300	147,0289	145,7405
330	42,8877	42,5146
360	-34,7422	-34,5548

Заметим, что наличие тормоза на форму графика почти не повлияло.

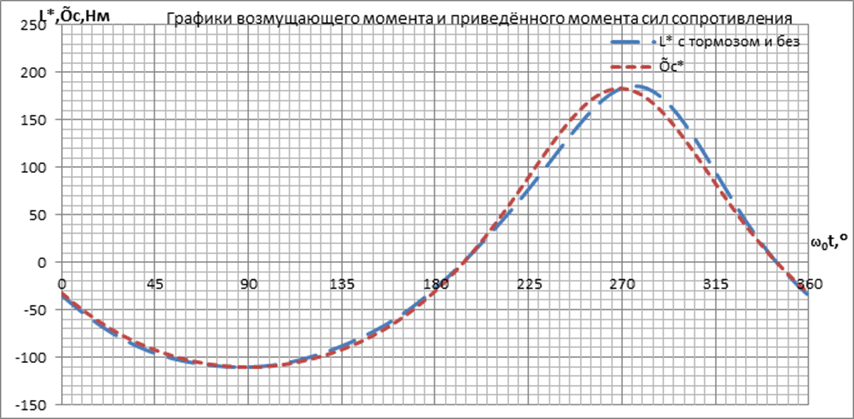
Видим, что графики возмущающего момента и приведённого момента