Математика \ Экономико-математические методы и модели в отрасли связи

Оптимизация сетевого графика при поточной организации работ на объекте. Расчет оптимального числа резервного оборудования в системах массового обслуживания

Страницы работы

20 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

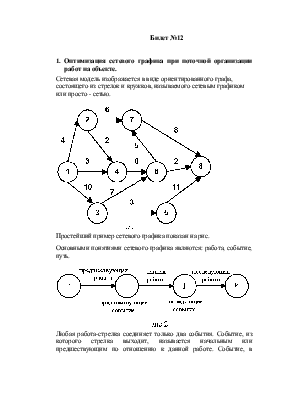
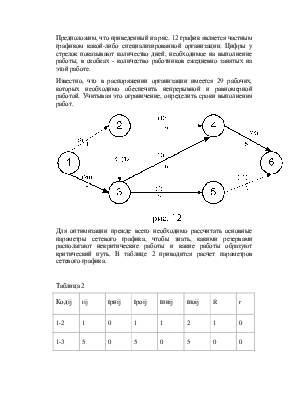
Последовательность выполнения любого специализированного потока по участкам рекомендуется принять в порядке возрастания ранних окончаний работ, т. е. сначала на 1, затем на П и наконец, на Ш участке.

Новый сетевой график строится с одноименным добавлением организационных связей, показывающих переход специализированных бригад с одного участка на другой.

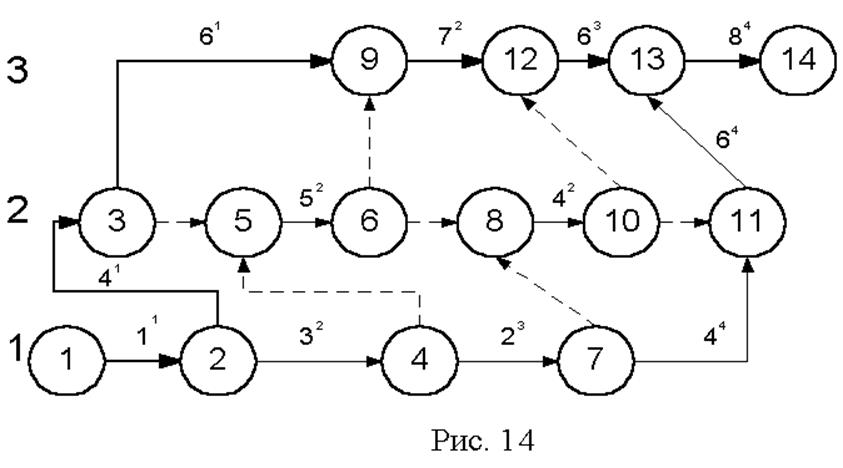
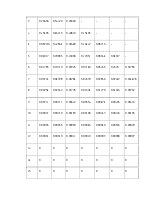
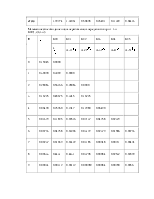
Нумерация событий в полученном сетевом графике производится заново. Далее рассчитываются параметры сетевого графика.

Таблица 4

Число предш. Работ	Код работ	tij	tрнij	tроij	tпнij	tпоij	Rij	rij
1	2	3	4	5	6	7	8	9
0	1-2	1	0	1	0	1	0	0
1	2-3	4	1	5	1	5	0	0
1	2-4	3	1	4	3	6	2	0
1	3-5	0	5	5	6	6	1	0
1	3-9	6	5	11	5	11	0	0
1	4-5	0	4	4	6	6	2	1
1	4-7	2	4	6	12	14	8	0
2	5-6	5	5	10	6	11	1	0
1	6-8	0	10	10	14	14	4	0
1	6-9	0	10	10	11	11	1	1
1	7-8	0	6	6	14	14	8	4
1	7-12	4	6	10	14	18	8	4
2	8-10	4	10	14	14	18	4	0
2	9-12	7	11	18	11	18	0	0
1	10-11	0	14	14	18	18	4	0
1	10-12	0	14	14	18	18	4	4
2	11-13	6	14	20	18	24	4	4
2	12-13	6	18	24	18	24	0	0
2	13-14	8	24	32	24	32	0	0

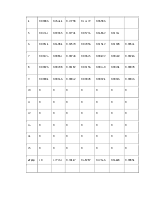
Новый критический путь равен 32 дням и проходит по всем трем участкам : вначале по 1, потом по П и затем по Ш.

2. Расчет оптимального числа резервного оборудования в системах массового обслуживания.

Наличие резервного оборудование как и увеличение числя обслуживаемых каналов способствует снижению коэффициента простоя оборудования. В то же время образование резервного парка оборудование требует значительных затрат на его приобретение и содержание. С увеличением единиц резервного оборудования сокращается математическое ожидание числа неработающего оборудования, а вместе с ним сокращаются издержки от простоя оборудования. Задача сводится к отысканию такого соотношения между числом обслуживаемых каналов и количеством резервного оборудования, при котором общая величина издержек предприятия Э(r,R) будет наименьшей. Целевая функция, как упоминалось, имеет вид:

С помощью зависимостей и определяется Р_k - вероятность нахождения в обслуживающей системе К - требований и Р₀- вероятность отсутствия требований в системе.

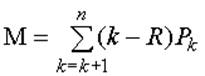
Математическое ожидание числа отказавших единиц оборудования, которое не может быть заменено резервным, когда запас полностью израсходован, определяется по формуле:

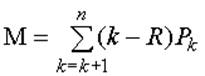
Пользуясь этой формулой в таблице 8 рассчитаем значение М для r=1, n=15, 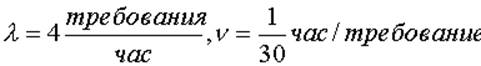и R=0,1,2,3,4, и 5.

Математическое ожидание числа работающих передатчиков при r=2 и R=0,1,2,3,4,5.

K			R=0	R=1	R=2	R=3	R=4	R=5
K			k	(k-1)	(k-2)	(k-3)	(k-4)	(k-5)
0	1,00000	0,09917	0	0	0	0	0	0
1	2,00000	0,19834	0,19834	0	0	0	0	0
2	1,86573	0,18502	0,37004	0,18502	0	0	0	0
3	1,61680	0,16033	0,48099	0,32066	0,16033	0	0	0
4	1,29214	0,12814	0,51256	0,38442	0,25628	0,12814	0	0
5	0,94747	0,09396	0,45980	0,37584	0,28188	0,18792	0,093396	0
6	0,63158	0,06263	0,37578	0,31315	0,25052	0,18789	0,12526	0,06263
7	0,37891	0,03757	0,26299	0,22542	0,18785	0,15028	0,11271	0,07514
8	0,20206	0,02003	0,16024	0,14021	0,12018	0,10015	0,08012	0,06009
9	0,09428	0,00934	0,08406	0,07472	0,06538	0,05604	0,04670	0,03736
10	0,03770	0,00373	0,03730	0,03357	0,02984	0,02611	0,02238	0,01865
11	0,01256	0,00124	0,01364	0,01240	0,01116	0,00992	0,00868	0,00744
12	0,00334	0,00033	0,00396	0,00363	0,00330	0,00297	0,00264	0,00231
13	0,00066	0,00006	0,00018	0,00072	0,00066	0,00060	0,00054	0
14	0,0008	0	0	0	0	0	0	0
15	0	0	0	0	0	0	0	0
итого	10,08331	0,99989	2,97048	2,06976	1,36738	0,85002	0,49299	0,26362

Расчёты математического числа неработающего оборудования при количестве электромехаников r=3,4,5 проводится в таблицах 9,10,11

Математическое ожидание числа неработающих передатчиков при r=3 и R=0,1,2,3,4 и 5 резервных

K		R=0	R=1	R=2	R=3	R=4	R=5
K		k=	(k-1)	(k-2)	(k-3)	(k-4)	(k-5)
0	0,14282	-	-	-	-	-	-
1	0,28564	0,28564	-	-	-	-	-
2	0,26666	0,53320	0,26660	-	-	-	-
3	0,15405	0,46215	0,30810	0,15405	-	-	-
4	0,082216	0,32864	0,24648	0,16432	0,08216	-	-
5	0,04017	0,20085	0,16068	0,12051	0,08034	0,04017	-
6	0,01785	0,10710	0,09925	0,07140	0,05355	0,3570	0,01785
7	0,00714	0,04998	0,04284	0,03570	0,02856	0,02142	0,014428
8	0,00254	0,02032	0,01778	0,01524	0,01270	0,01016	0,00762
9	0,00711	0,00711	0,00632	0,00553	0,00474	0,00395	0,00316
10	0,00021	0,00210	0,00189	0,00168	0,00147	0,00126	0,00105
11	0,00005	0,00055	0,00050	0,00045	0,00040	0,00035	0,00020
12	0,00001	0,00010	0,00011	0,00010	0,00009	0,00008	0,00007
13	0	0	0	0	0	0	0
14	0	0	0	0	0	0	0
15	0	0	0	0	0	0	0
итого		1,99774	1,14061	0,56898	0,26401	0,11309	0,04423

Математическое ожидание числа неработающих передатчиков при r=4 и R=0,1,2,3,4 и 5

K		R=0	R=1	R=2	R=3	R=4	R=5
K		k	(k-1)	(k-2)	(k-3)	(k-4)	(k-5)
0	0,15045	0,0000
1	0,30090	0,3009	0,0000
2	0,28083	0,56166	0,28083	0,0000
3	0,16225	0,48675	0,3245	0,16225
4	0,06490	0,25960	0,1947	0,12980	0,06490
5	0,02379	0,11895	0,09516	0,07137	0,04758	0,02379
6	0,00793	0,04758	0,03965	0,03172	0,02379	0,01586	0,00793
7	0,00237	0,01659	0,01422	0,01185	0,00948	0,00711	0,00474
8	0,00633	0,4431	0,4431	0,03798	0,00084	0,02532	0,01899
9	0,00014	0,00112	0,00112	0,000989	0,00084	0,00700	0,0056
10	0,00002	0,0002	0,00018	0,00016	0,00014	0,00012	0,0010
11	0	0	0	0	0	0	0
12	0	0	0	0	0	0	0
13	0	0	0	0	0	0	0
14	0	0	0	0	0	0	0
15	0	0	0	0	0	0	0
итого	1,0	1,84235	0,99629	0,44611	0,17858	0,0792	0,03232

Математическое ожидание числа неработающих передатчиков при r=5 и R=0,1,2,3,4 и 5

K			R=0		R=1		R=2		R=3		R=4		R=5
			k		(k-1)		(k-2)		(k-3)		(k-4)		(k-5)
0	0,15277
1	0,30554		0,30554
2	0,28509		0,57018		0,28509
3	0,16467		0,49401		0,32934		0,16467
4	0,06586		0,26344		0,19758		0,13172		0,06586
5	0,01931		0,09655		0,07724		0,05793		0,03862		0.01931
6	0,00514		0,03084		0,02570		0,02056		0,01542		0,01028		0,00514
7	0,00123		0,00861		0,00738		0,00615		0,00492		0,00369		0,00246
8	0,00026		0,00208		0,00182		0,00156		0,00130		0,00104		0,00078
9	0,00004		0,00036		0,00032		0,00028		0,00024		0,00016		0,00016
10	0		0		0		0		0		0		0
11	0		0		0		0		0		0		0
12	0		0		0		0		0		0		0
13	0		0		0		0		0		0		0
14	0		0		0		0		0		0		0
15	0		0		0		0		0		0		0
итого	1,0		1,77161		0,92447		0,38287		0,12636		0,03448		0,00854

		0		1		2		3		4		5

2		2,97048		2,06976		1,36738		0,85002		0,49299		0,26362
3		1,99774		1,14061		0,56898		0,26401		0,11309		0,04423
4		1,84235		0,99629		0,44611		0,17858		0,0792		0,03232
5		1,77161		0,922447		0,38287		0,12636		0,03448		0,00854

3. Задача:

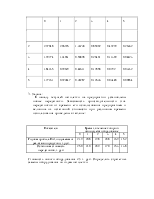
К началу текущей пятилетки на предприятии установлены новые передатчики. Зависимость производительности этих передатчиков от времени его использования предприятием и величина их остаточной стоимости при различном времени использования приведены в таблице:

Показатели	Время t, в течение которого используется оборудование
Показатели	0	1	2	3	4	5
Годовая прибыль П(t), получаемая от реализации продукции, т. руб.	21,9	20,8	19,8	18,8	16,9	15,2
Остаточная стоимость передатчиков, т. руб.	25,0	21,0	18,9	17,0	15,3	13,8

Стоимость нового оборудования 25 т. руб. Определить стратегию замены оборудования по годам пятилетки.

Для начала посчитаем прибыль в зависимости от срока работы без замен

Прибыль считается так: минус 25 на новое оборудование, плюс сумма годовой прибыли (в зависимости от срока работы) и плюс остаточная стоимость оборудования например: если мы считаем прибыль для трех лет работы:

С(t)= -25 + (20,8+19,8+18,8) +17 = 51,4

формула для расчета прибыли:

срок работы, t	1	2	3	4	5
годовая прибыль, П(t)	20,8	19,8	18,8	16,9	15,2
остаточная стоимость, О(t)	21	18,9	17	15,3	13,8
суммарная прибыль, C(t)	16,8	34,5	51,4	66,6	80,3

Замены возможны: после работы 1 год, после 2ух лет работы, после 3-ех, и после 4ех лет работы. Замена сразу и замена после 5-ти лет работы эквивалентны работе без замен.

Возможные количества замен: 0, 1, 2, 3 и 4.

Прибыль зависит только от срока работы (например, при работе 3 года, потом замена, потом ещё два года и при работе два года, потом замена, потом ещё три года прибыль будет одинаковая)

Поэтому нам нужно считать только разбиения пятилетки на разные промежутки времени, без учета порядка.

число замен	возможные варианты работы (без учета порядка)	разбиение
0	без замен 5 лет подряд	5
1	4 года работы, замена, ещё 1 год работы	4+1
1	3 года работы, замена, ещё 2 года работы	3+2
2	2 года работы, замена, еще 2 года, замена, еще 1 год	2+2+1
2	3 года работы, замена, ещё 1 год, замена, еще 1 год	3+1+1
3	1 год, замена, 1 год, замена, 1 год, замена, два года	1+1+1+2
4	замена после каждого года работы	1+1+1+1+1

Прибыль при работе без замен мы уже считали: это C(t=5) 80,3

Прибыль при работе по схеме 4+1 это прибыль от работы 4 года без замены плюс прибыль от работы один год без замены, т.е. C(t=4)+C(t=1)= 66,6+16,8=83,4

и так далее:

Итоговая прибыль в зависимости от схемы работы: