Министерство Российской Федерации по связи и информатизации
Сибирский Государственный Университет телекоммуникаций и информатики
Кафедра АЭС
КУРСОВАЯ РАБОТА ПО КУРСУ
ТЕОРИИ ТЕЛЕТРАФИКА
ВАРИАНТ №17
Выполнил: .
Группа: А-47
Проверил:
Новосибирск 2007
Содержание.
Введение стр.3
Задача №1 стр. 4
Задача №2 стр. 8
Задача №3 стр. 9
Задача №4 стр. 14
Задача №5 стр. 16
Задача №6 стр. 17
Задача №7 стр. 19
Задача №8 стр. 21
Задача №9 стр. 27
Список литературы стр. 30
Введение.
Теория телетрафика относится к сравнительно недавно возникшей и интенсивно развивающейся области математики - теории массового обслуживания.
Основной целью теории телетрафика является разработка математических методов определения основных методов определения основных характеристик обслуживания потоков вызовов в сетях электросвязи.
Тесно переплетаясь с теорией массового обслуживания, теория телетрафика отличается от нее конкретностью результатов анализа. Это достигается широким использованием наряду с аналитическим методом, методов статистического моделирования с целью оценки качества функционирования исследуемых систем, а также приближенных аналитических методов расчета, основанных на ряде упрощающих предположений.
С более общий позиций теория телетрафика является частью технической кибернетики и занимается исследованием структурно- сложных систем и сетей автоматической коммутации.
Появившись в двадцатые годы прошлого веки, благодаря работам А.К. Эрланга, теория телетрафика в последнее десятилетие претерпела существенные изменения. Это объясняется разработкой и широким вводом в коммерческую эксплуатацию цифровых систем коммутации (ЦСК) и цифровых сетей интегрального обслуживания (ЦСИО).
Наряду с коммутацией каналов в традиционных сетях электросвязи, в глобальной сети INТЕАNЕТ, локальных вычислительных сетях типа ENTERNET, сетях IP-телефонии используется коммутация пакетов. Это обстоятельство приводит к качественному изменению свойств и характеристик как потоков вызовов, так и нагрузки в сетях связи. Как показали исследования, проведенные в последние годы , классическая гипотеза о простейшем потоке и пуассоновской нагрузке в цифровых мультисервисньх телекоммуникационных сетях не выполняется. Это обстоятельство послужило толчком для дальнейшем развития теории телетрафика, которое выразилась в разработке принципиально новых математических моделей потоков вызовов, нагрузки и процессов обслуживания в сетях связи.
Задача №1
На коммутационную систему поступает поток вызовов, создающий нагрузку Y эрланг. Определить вероятности поступления ровно i вызовов Pi (i=0, 1, 2 ...N) при примитивном потоке от N источников и Pi ( i=0,1, 2...j...) при простейшем потоке вызовов. Построить кривые распределения вероятностей Pi =f ( i ) и произвести сравнение полученных результатов.
Исходные данные: Y=3,5 Эрл; N=7.
1)Простейший поток вызовов.
Математической моделью простейшего потока вызовов является формула Пуассона:
Она определяет вероятность поступления точно i вызовов при
простейшем потоке с параметром 
за интервал времени t. Если мы
возьмём t=1 то формула Пуассона примет вид:
Интенсивность простейшего потока вызовов количественно
совпадает с его параметром, т.е. 
. Величину поступающей нагрузки определим по формуле 
. Учитывая, что t=1 и
., параметр численно совпадает c величиной поступающей
нагрузки или
.
Определим вероятность P0 по этой формуле, а остальные вероятности определим по первой рекуррентной формуле:
Расчет:
K=0, 
K=1, 
K=2, 
K=3, 
K=4, 
K=5, 
K=6, 
=
,число близкое к 1
2)Примитивный поток вызовов.
При примитивном потоке от N источников вероятность поступления точно i вызовов определяется по формуле Бернулли:
- удельная нагрузка от одного источника.
Значение Р0 определим с помощью формулы Бернулли , а остальные значения по рекурсивной формуле , для простоты расчетов.
- рекурсивная формула.
Рассчет:
k=0 
k=1 
k=2
k=3 
k=4 
k=5 
k=6 
Проверим результат :
-результат близок к 1.
Построю кривые распределения вероятностей Pi =f ( i ) :
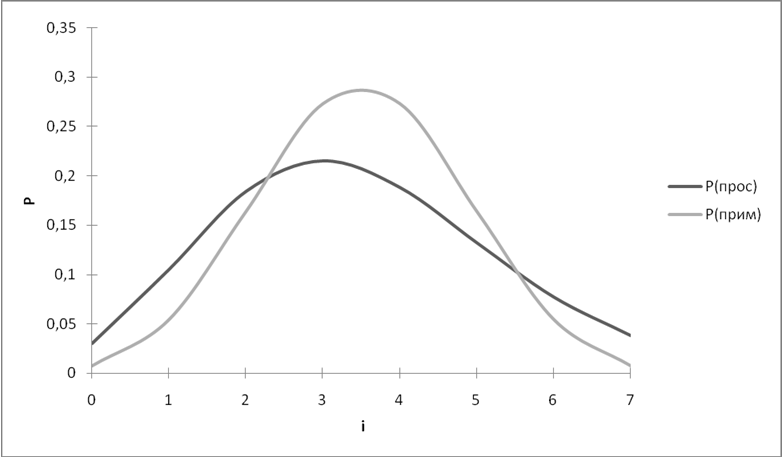
Вывод:
1)
S1 
S2 -по условию нормировки;
2) На отрезке [0 ;2.3]- Pi(прост)> Рi(прим) ;
на отрезке [2.3; 5.8]- Pi(прост)<Рi(прим);
на отрезке [5.8; 
]- Pi(прост)> Рi(прим).
3)Интенсивность поступающей нагрузки количественно совпадает со средним числом вызовов поступивших на единичном интервале (среднее время обслуживания одного вызова):
Для простейшего потока –
=
=1*0.105+2*0,184+3*0,215+4*0,188+5*0,132+6*0,077+
+7*0,038≈3,5=Y
Для примитивного потока –
=
=1*0.0547+2*0,164+3*0,273+4*0,273+5*0,164+6*0,0547+
+7*0,00781≈3,5=Y
Таким образом выполняется 3-е толкование нагрузки, следовательно расчет сделан правильно.
Задача №2
Пучок ИШК координатной станции типа АТСК -Y обслуживает абонентов одного блока АИ. Определить поступающую на этот пучок нагрузку Y, если число абонентов, включенных в блок, N=1000, среднее число вызовов от одного абонента С, среднее время разговора Т , доля вызовов закончившихся разговором PP .
Исходные данные: С=3,5 
; Т= 90с ; Рр =0,7 ; N=1000.
Решение:
Для определения телефонной нагрузки воспользуемся формулой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
