



























































Обозначим G– размер комиссионных, g – ставка комиссионных. Тогда G = S(0)g. Наращение по ставке iэф величины (S(0) – G) дает наращенную сумму S(T) = S(0) (1+iT), если iэф – ставка простых процентов:
(S(0) – G) (1+ iэф Т) = S(T)
S(0) (1-g) (1+ iэф Т) =S(0) (1+iT).
Сделав преобразование получаем формулу для эффективной ставки простых процентов:
iэф = 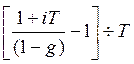 .
.
Если доходность измеряется в виде эффективной ставки сложных процентов, то соответствующая формула имеет вид:
iэф.сл. = 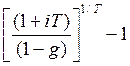 .
.
Пример 29.
Кредит выдан на 180 дней по ставке 80% годовых с удержанием комиссионных 2% от его суммы. Определить доходность кредитной операции с учетом удержания комиссионных при расчетном количестве дней в году 360.
Решение.
Доходность по простой ставке рассчитывается
iэф = 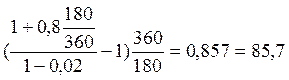 %.
%.
Доходность по сложной процентной ставке равна:
iэф.сл. = 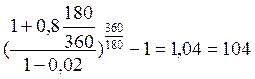 %
%
Заметим, что ставки 85,7% и 104% являются эквивалентными и показывают равную доходность финансовой операции.
Если бы банк не удерживал комиссионные, то эффективность была равна 80% годовых.
Учетные операции
При учете векселя комиссионные удерживаются с величины S(T), то есть сумма комиссионных равнаG=S(T)g. Балансовое уравнение для вывода формулы эффективной ставки простых процентов имеет вид:
(S(0)-G) (1+ iэфT) = S(T)
Учитывая, что S(0) = S(T) (1-dT), величину (S(0)-G) определим как S(T) (1-dT-g). Тогда балансовое уравнение имеет вид:
S(T) (1-dT-g) (1+ iэфT) = S(T)
Откуда получаем формулу для iэф:
iэф = ![]() .
.
Если доходность измеряется по сложной ставке, то
iэф.сл. = ![]() .
.
6.3. Доходность операций с ценными бумагами
При покупке ценных бумаг возможно получение дополнительного дохода или сохранение капитала от обесценения в условиях инфляции.
Расчет дохода по различным видам ценных бумаг производится на основе формул наращения и дисконтирования по процентной ставке. (Формулы приведены в соответствующих таблицах Справочника ЭУМК).
Рассмотрим следующие примеры.
Пример 30.
Депозитный сертификат номиналом 100 000 руб. выдан 14 мая на полгода с начислением по нему процентов по ставке 18 % годовых. Определить сумму дохода и сумму погашения долгового обязательства.
Решение:
Если начисляются точные проценты, то К = 365 и при использовании английской схемы начисления простых процентов точное число дней можно определить по специальной таблице. (См. таблицу определения порядковых дней в году в Справочнике ЭУМК). Оно составляет 184 дня.
Если используется германская схема начисления процентов, то срок составляет 6 × 30 = 180 дней.
На основе формул наращения по простой процентной ставке, приведенной в Справочнике ЭУМК, рассчитаем доход на сумму долга.
Для английской схемы:
I
= 100000 × 0,18 ×![]() = 9074 (руб.)
= 9074 (руб.)
S(T) = 100000 + 9074 = 109074 (руб.)
Для германской схемы:
I
= 100000 × 0,18 ×![]() = 9000 (руб.)
= 9000 (руб.)
S(T) = 100000 + 9000 = 109000 (руб.)
Пример 31.
Платежное обязательство выдано на пять месяцев под 20 % годовых с погашением 200000 руб. Определить доход владельца данного платежного обязательства.
Решение:
По формуле дисконтирования рассчитаем современную стоимость обязательства:
S(o)
= 200000 / (1 + 0,2 ×![]() )= 184672 (руб.)
)= 184672 (руб.)
I = 200000 – 184672 = 15328 (руб.)
Пример 32.
Сертификат номинальной стоимостью 150000 руб. выдан на 200 дней (К = 365) с погашением 180000 руб. Определить доходность сертификата в виде простой ставки ссудного процента.
Решение:
Определим процентную ставку iиз уравнения:
180000 = 150000 (1 + i ×![]() )
)
i = (180000 / 150000 – 1) ×365 / 200 = 36,5%
Покупка и продажа векселя с использованием простой учетной ставки
Доходность этой финансовой операции связана с разностью цен купли-продажи, которая зависит от сроков погашения векселя и уровнем учетных ставок в момент купли-продажи векселя. Обозначим S – номинал векселя, d1 – учетная ставка, по которой его учел банк за время t1 до его погашения. Тогда цена покупки P1 банком равна P1 = S (1- d1t1).
Банк продал вексель за время t2 до его погашения по ставке d2. Цена продажи P2 равна P2 = S (1- d2t2).
Таким образом, вексель куплен по цене P1 и продан по цене P2 через срок (t1-t2) дней. Доход от купли-продажи векселя равен P2 - P1.
Эффективность операции за срок (t1-t2) выражается в виде процентной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.