Формирование требований и разработка концептуальной модели. Границы модели и внешней среды

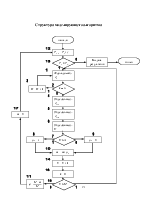
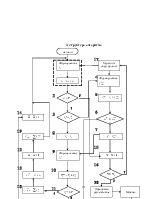
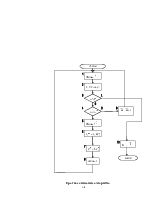
случай проигрыша (стороной B) ищется оптимальная стратегия в следующей последовательности:

1.  Сторона B в каждом столбце платежной матрицы находит максимальный элемент.

2.  Из всех максимальных элементов выбирается минимальный элемент, который определяет оптимальную стратегию проигрывающей стороны.

Математически это оформляется следующим образом:

-минимаксный проигрыш (верхняя цена игры).

Если , то игра считается равновесной. Это значит, что сторонам, участвующим в конфликте, известно о поведении противника. По модели равновесная игра определяется наличием в матрице седловой точки, когда минимальный элемент i-ой строки равен максимальному элементу j-го столбца. Такая игра еще называется чистой игрой, а выбранные стратегии называются оптимальными.

В большинстве случаев  седловая точка в платежной матрице отсутствует, т.е. . Это говорит о том, что противоположная сторона не имеет полной информации о стратегии противника. В этом случае о применении противоположной стороной стратегии можно говорить только с вероятностью. Поэтому в таких играх определяется не столько выигрышпроигрыш, сколько вероятность применения противником той или иной стратегии. Выбрать наилучшую стратегию, значит выбрать ту стратегию, у которой максимальная вероятность. Для этого на основе известной платежной матрицы определяется ряд распределения вероятностей для каждой из сторон:

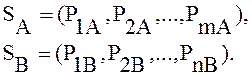
В такой игре можно говорить только о среднем платеже (математическом ожидании платежа)

, где - платежи игровой матрицы, - вероятности применения сторонами i-ой  и  j-ой стратегии.

Для стороны А оптимальная стратегия определится по  среднему платежу

.

Для стороны B оптимальная стратегия определится по среднему платежу

.

В практических задачах находят средний ожидаемый выигрыш-проигрыш (цену игры) из формулы , где .

Методы решения игровой задачи

1.  Если в платежной матрице имеется седловая точка, то ее определяют простым перебором.

2.  Если платежная матрица не имеет седловой точки, следовательно,  игра смешанная, и необходимо найти ряды распределения вероятностей применения сторонами A и B стратегий  и .

Методика решения смешанной игры 2x2

Решением смешанной игры 2х2 является определение двух рядов распределения вероятностей применения сторонами A и B стратегий:

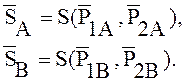
Определение ряда ведется в следующей последовательности:

1.  Строится ряд распределения для стороны A. Если сторона A будет использовать наилучшую свою стратегию , то при любой стратегии противника ее выигрыш составит величину . Исходя из этого, можно составить систему линейных алгебраических уравнений, в которых в качестве переменных фигурируют вероятности применения  противником той или иной стратегии

выигрыш при применении стороной B стратегии , выигрыш при применении стороной B стратегии .

2.  По тому же принципу можно составить систему линейных алгебраических уравнений для стороны B:

выигрыш при применении стороной A стратегии , выигрыш при применении стороной A стратегии .

3.  Решая полученные системы, найдем вероятности .

4.  Если принять , , то решение запишется в виде:

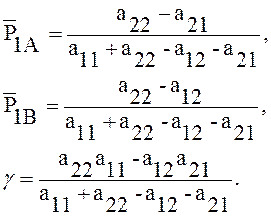
Пример решения игры 22

Допустим, платежная матрица игры имеет вид:

Из матрицы видно, что нижняя цена игры , верхняя цена игры ,  седловой точки нет. Значит, игра смешанная и необходимо найти вероятности .

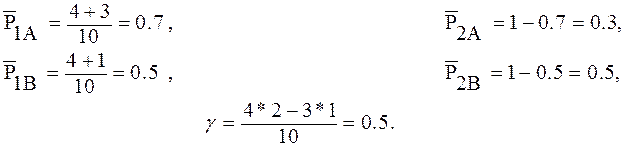
В результате решения получим два ряда распределения вероятностей:

.

Из этого следует, что стороне А необходимо применять стратегию  , а стороне В чередовать стратегии с одинаковой частотой.

Методика решения смешанной игры mxn

Целью является поиск рядов распределения вероятностей для стороны A размерностью m и для стороны B размерностью n. Для поиска указанных рядов в соответствии с выше рассмотренным принципом строится система линейных алгебраических уравнений вида:

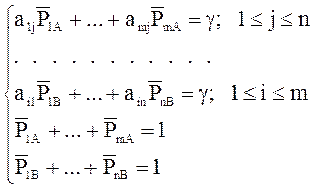
Решением данной системы будет .

Решить данную систему можно средствами линейного программирования