Моделирование нелинейных динамических систем. Исследуемая система управления. Нелинейный элемент

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

ОТЧЁТ

о лабораторной работе №2

«Моделирование нелинейных

динамических систем».

13 вариант

Работу выполнила студентка группы №4081/2

Преподаватель

__________________

Санкт-Петербург

2011 г.

1. Цель работы: исследовать нелинейную систему управления.

2. Выполнение работы:

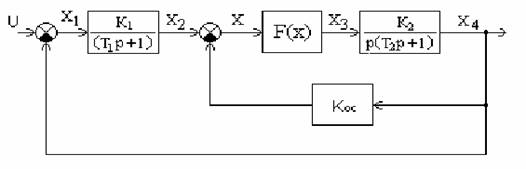
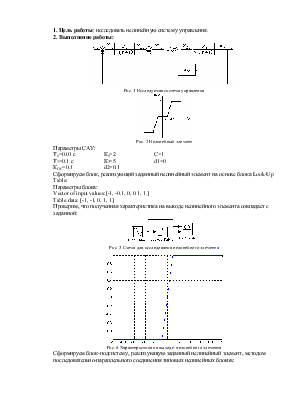
Рис. 1 Исследуемая система управления

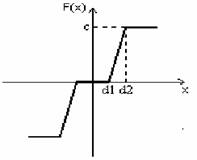
Рис. 2 Нелинейный элемент

Параметры САУ:

Т₁=0.01 с                    К₁=2                           С=1

Т₂=0.1 с                      К₂=5                           d1=0

К_OC=0.1                      d2=0.1

Сформируем блок, реализующий заданный нелинейный элемент на основе блока Look-Up Table:

Параметры блока:

Vector of input values:[-1, -0.1, 0, 0.1, 1 ]

Table data: [-1, -1, 0, 1, 1]

Проверим, что полученная характеристика на выходе нелинейного элемента совпадает с заданной:

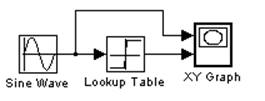
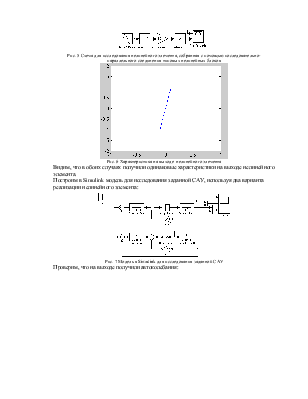
Рис. 3 Схема для исследования нелинейного элемента

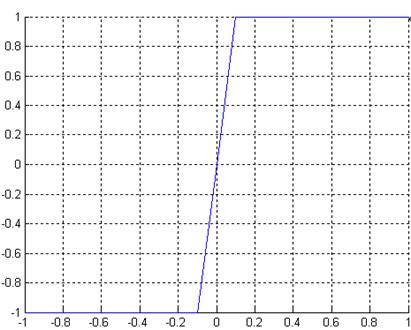
Рис. 4 Характеристика на выходе  нелинейного элемента

Сформируем блок-подсистему, реализующую заданный нелинейный элемент, методом последовательно-параллельного соединения типовых нелинейных блоков:

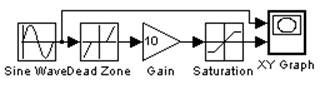
Рис. 5 Схема для исследования нелинейного элемента, собранная с помощью последовательно-параллельного соединения типовых нелинейных блоков

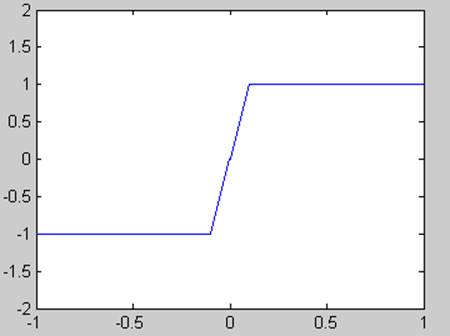
Рис. 6 Характеристика на выходе  нелинейного элемента

Видим, что в обоих случаях получили одинаковые характеристики на выходе нелинейного элемента.

Построим в Simulink модель для исследования заданной САУ, используя два варианта реализации нелинейного элемента:

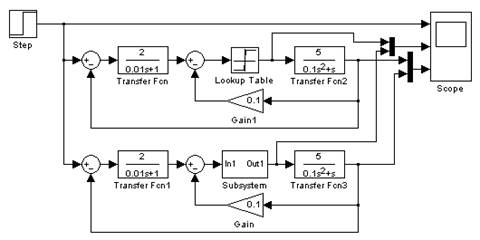
Рис. 7 Модель в Simulink для исследования заданной САУ

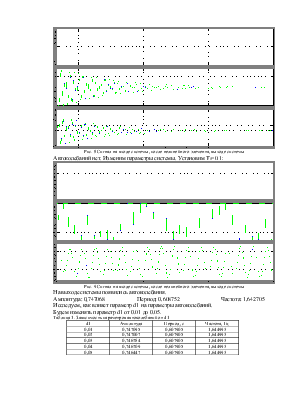
Проверим, что на выходе получили автоколебания:

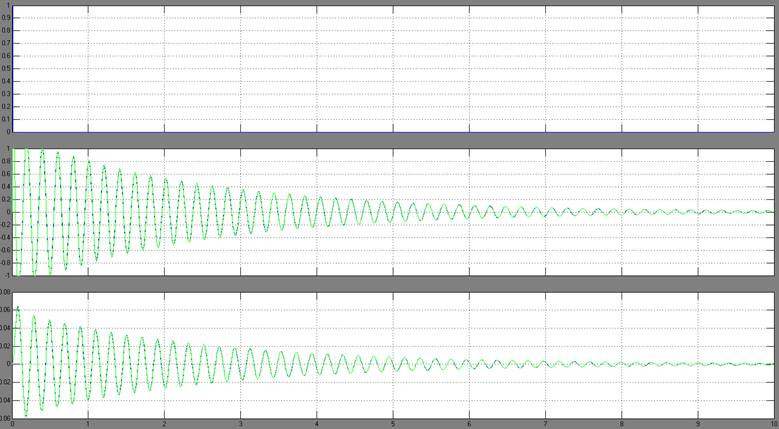
Рис. 8 Сигнал на входе системы, после нелинейного элемента, выходе системы

Автоколебаний нет. Изменим параметры системы. Установим Т₁=0.1:

Рис. 9 Сигнал на входе системы, после нелинейного элемента, выходе системы

На выходе системы появились автоколебания.

Амплитуда: 0,747068                       Период: 0,608752                             Частота: 1,642705

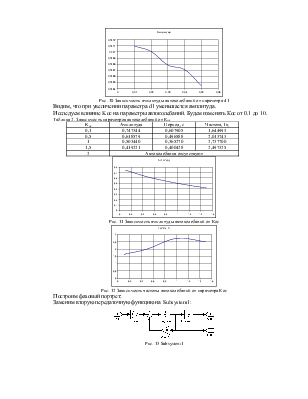
Исследуем, как влияет параметр d1 на параметры автоколебаний.

Будем изменять параметр d1 от 0.01 до 0.05.

Таблица 1. Зависимость параметров автоколебаний от d1

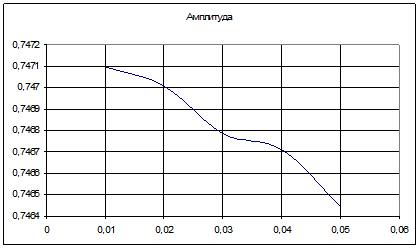
Рис. 10 Зависимость амплитуды автоколебаний от параметра d1

Видим, что при увеличении параметра d1 уменьшается амплитуда.

Исследуем влияние Kос на параметры автоколебаний. Будем изменять Кос от 0.1 до 10.

Таблица 2. Зависимость параметров автоколебаний от К_ос

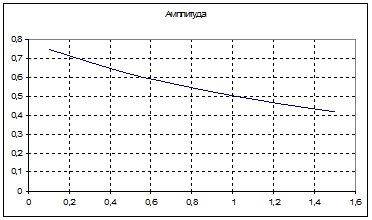
Рис. 11 Зависимость амплитуды автоколебаний от Кос

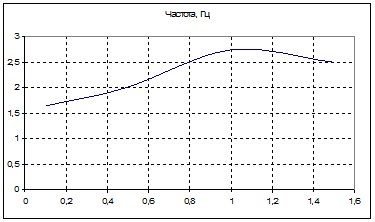
Рис. 12 Зависимость частоты автоколебаний от параметра Кос

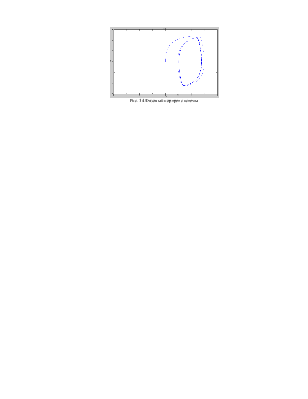
Построим фазовый портрет:

Заменим вторую передаточную функцию на Subsystem1:

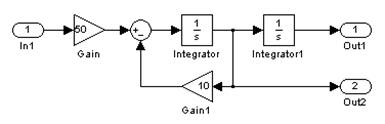
Рис. 13 Subsystem1

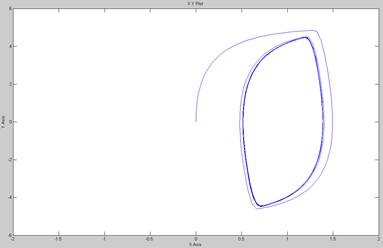
Рис. 14 Фазовый портрет системы