Моделирование детерминированных процессов. Начальные значения для интеграторов. Обратное преобразование Лапласа

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Автоматики и Вычислительной Техники

Отчет

о лабораторной работе №5

Дисциплина: “Моделирование систем управления”

Тема: “Моделирование детерминированных процессов”.

                                                                       Выполнил студент 4081/1  

группа               Ф.И.О.

Преподаватель _________________

подпись                    Ф.И.О.

Санкт-Петербург

2007

1. Задание

a = 0.6, b = 0.3, c = 0.4

2. Выполнение

2.1. g0

1)

2)

Тогда начальные условия

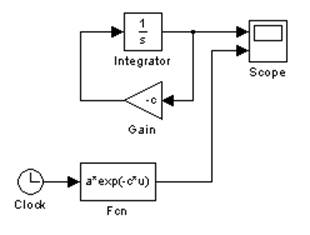
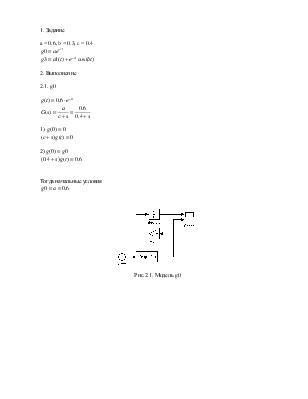
Рис.2.1. Модель g0

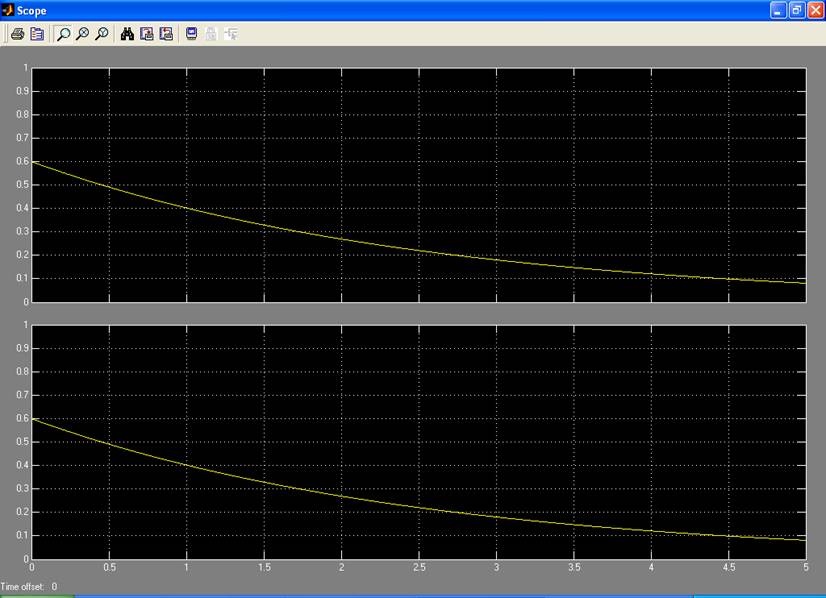
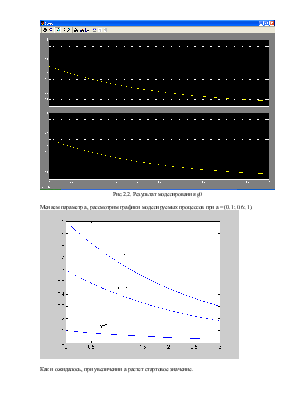
Рис.2.2. Результат моделирования g0

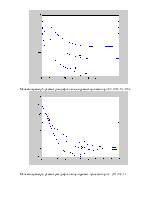
Меняем параметр а, рассмотрим графики моделируемых процессов при а = (0.1; 0.6; 1).

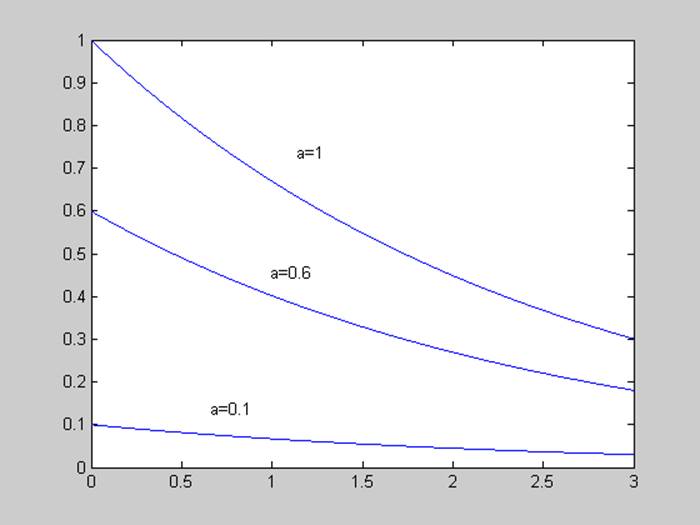
Как и ожидалось, при увеличении а растет стартовое значение.

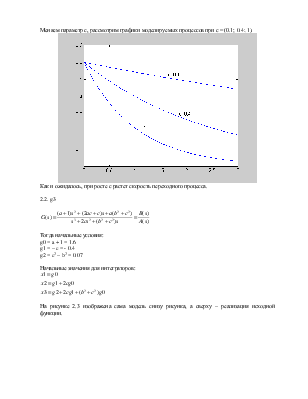
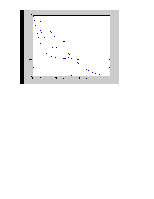
Меняем параметр с, рассмотрим графики моделируемых процессов при с = (0.1; 0.4; 1).

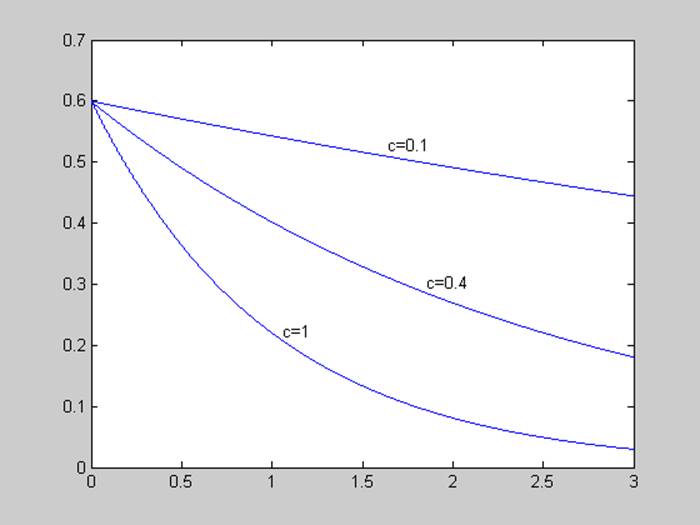
Как и ожидалось, при росте с растет скорость переходного процесса.

2.2. g3

Тогда начальные условия:

g0 = a + 1 = 1.6

g1 = – c = - 0.4

g2 = c² – b² = 0.07

Начальные значения для интеграторов:

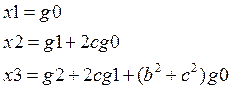
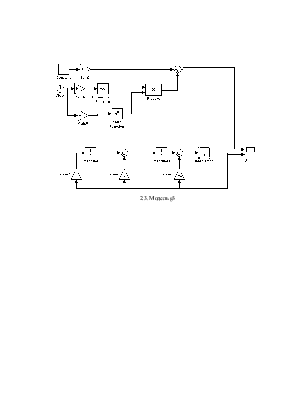
На рисунке 2.3 изображена сама модель снизу рисунка, а сверху – реализация исходной функции.

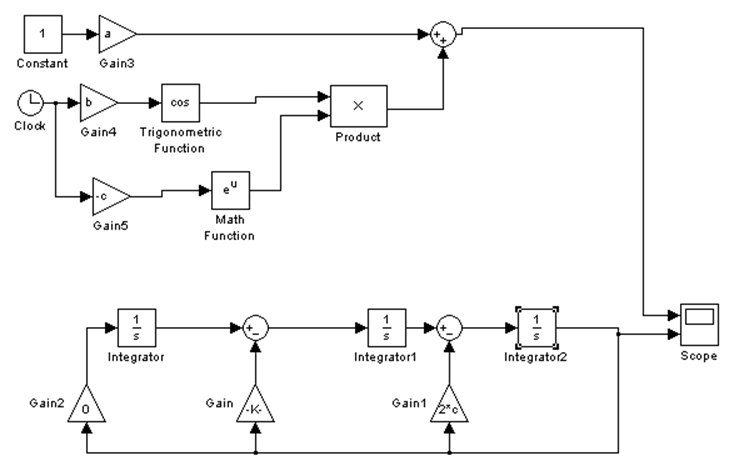
2.3. Модель g3

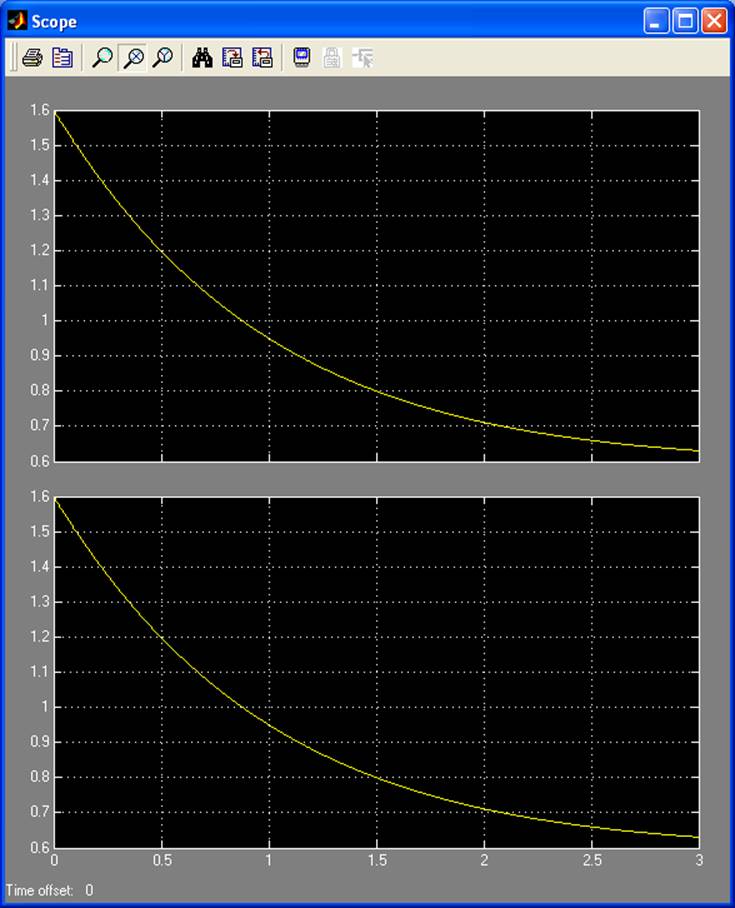
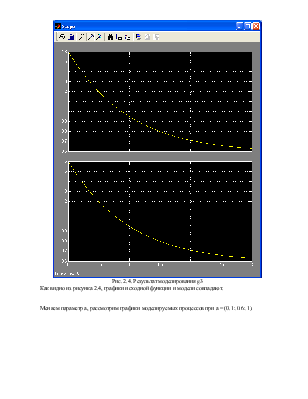
Рис. 2.4. Результат моделирования g3

Как видно из рисунка 2.4, графики исходной функции и модели совпадают.

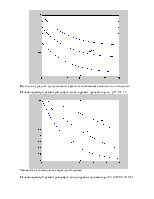
Меняем параметр а, рассмотрим графики моделируемых процессов при а = (0.1; 0.6; 1).

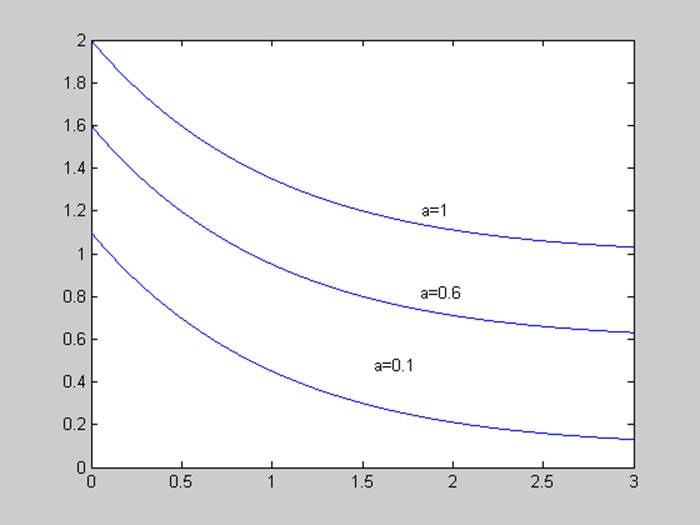
Как видно из рисунка, при увеличении а растет становившееся значение, что и ожидалось.

Меняем параметр с, рассмотрим графики моделируемых процессов при с = (0.1; 0.4; 1).

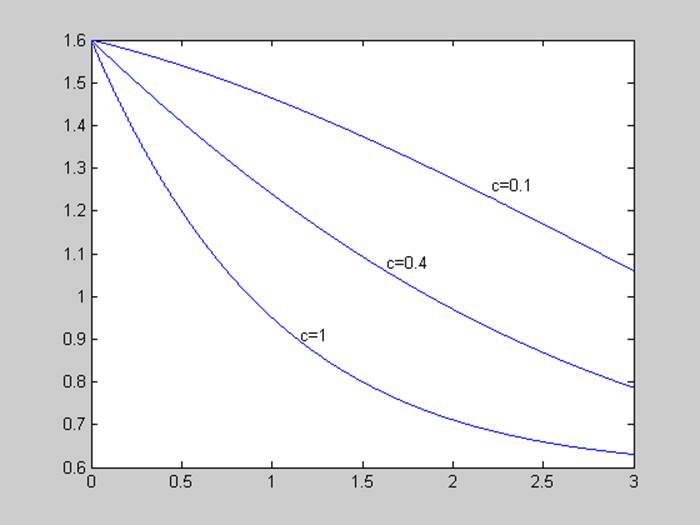
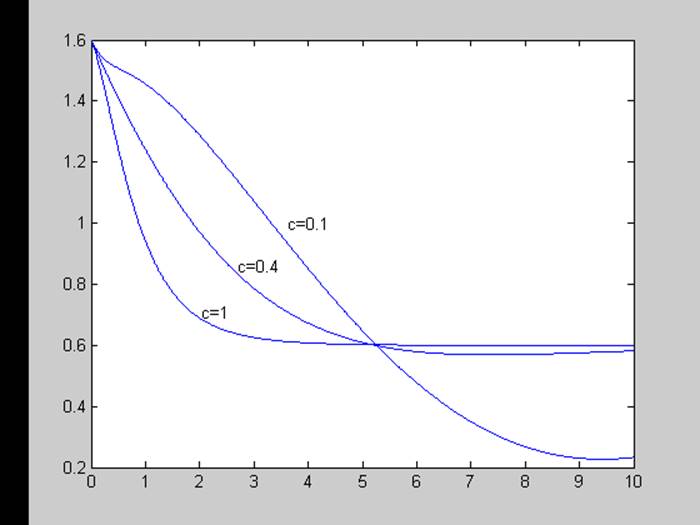
Чем меньше с, тем медленнее переходный процесс.

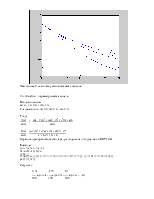
Меняем параметр b, рассмотрим графики моделируемых процессов при b = (0.025; 0.25; 0.5).

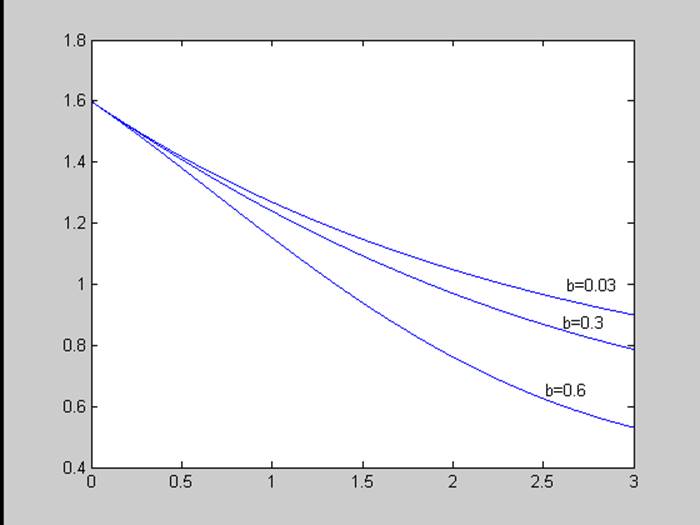
Чем больше b, тем ниже установившееся значение.

2.3. Линейно – параметрическая модель.

Вводим полином

Следовательно, m1 = 6, m2 = 11, m3 = 6

Тогда

Обратное преобразование Лапласа для получения σ(t) делалось в MATLAB

Команды:

a=0.25;b=0.25;c=1

m1=6;m2=11;m3=6

syms s

ilaplace(((a+1)*s^2+(2*a*c+c)*s+a*(b^2+c^2))/(s^3+m1*s^2+m2*s+m3))

pretty(ans)

Результат:

1191                479                 87

---- exp(-3 t) - --- exp(-2 t) + --- exp(-t) = σ(t)

200                 100                 200

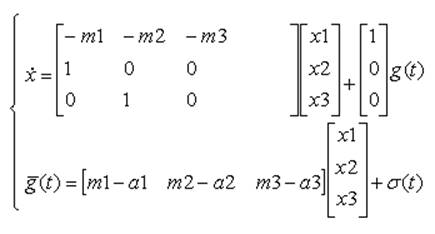
Структура дифференциальной динамической модели детерминированного процесса g3(t):

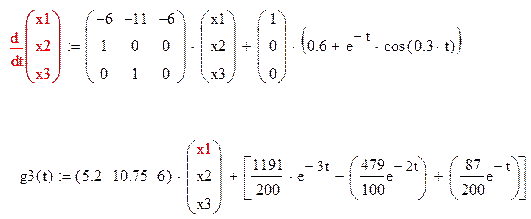
Модель:

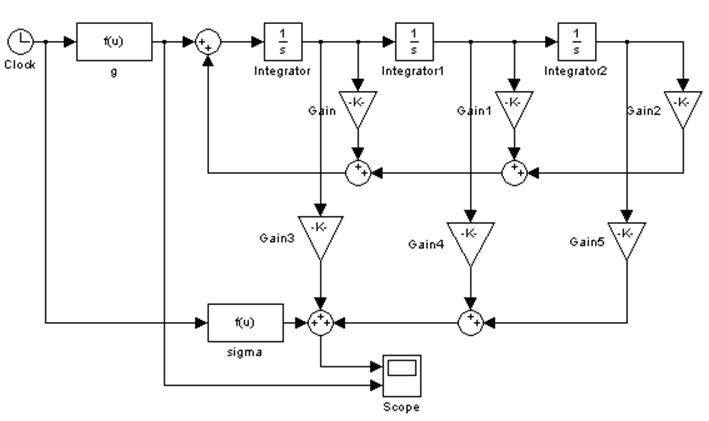
Рис. 2.5. Линейно – параметрическая модель g3

Результат:

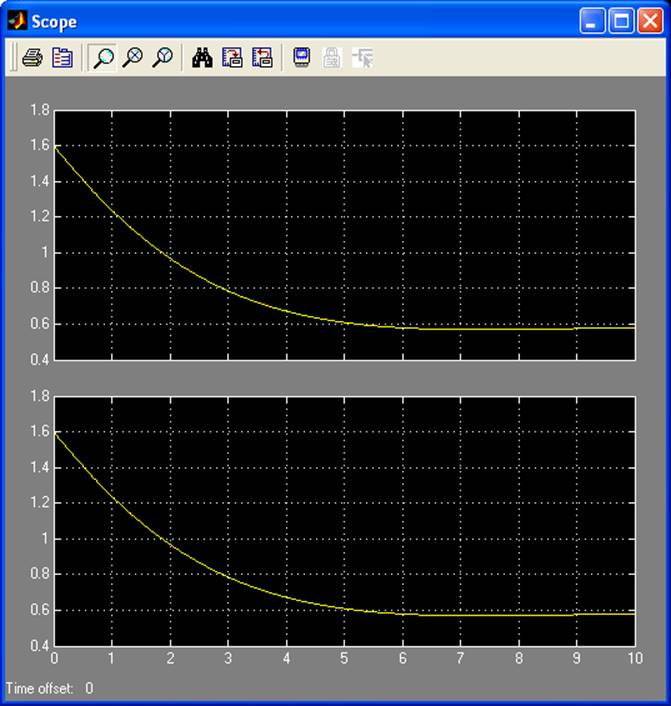
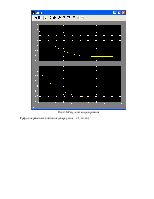
Рис. 2.6. Результат моделирования

График переменных состояния (сверху вниз – х1, х2, х3):

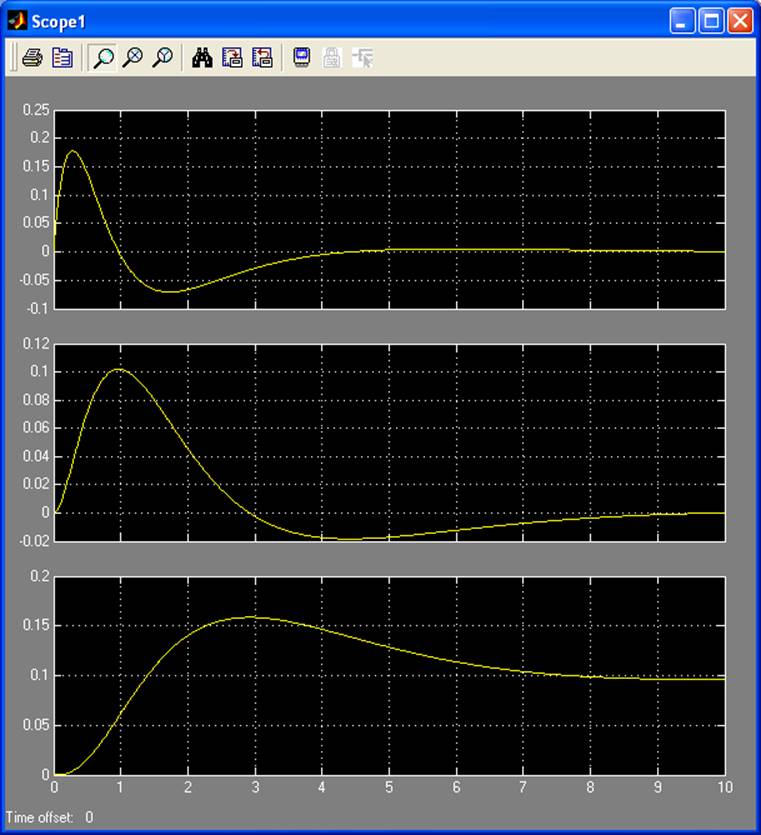
На рисунке 2.6 верхний график – результат моделирования, нижний – исходная функция.

Меняем параметр а, рассмотрим графики моделируемых процессов при а = (0.1; 0.6; 1).

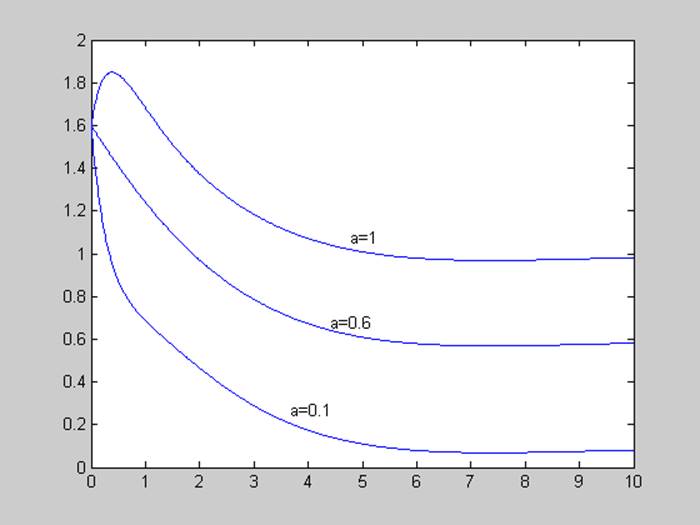
Меняем параметр b, рассмотрим графики моделируемых процессов при b = (0.03; 0.3; 0.6).

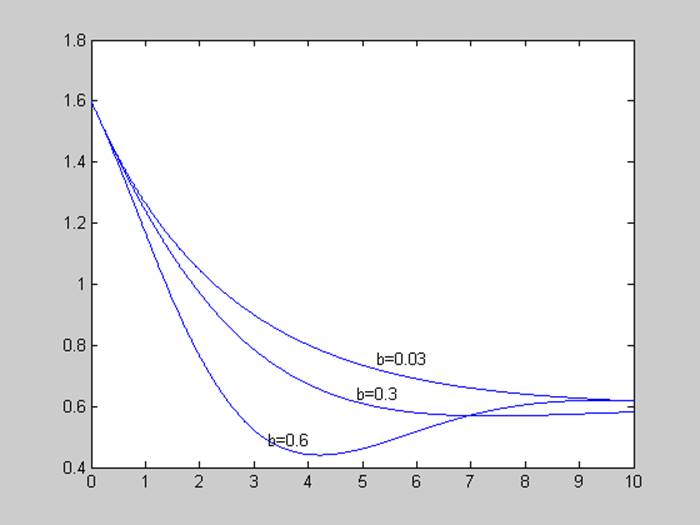
Меняем параметр с, рассмотрим графики моделируемых процессов при с = (0.1; 0.4; 1).