28. Задача оптимизации производственной программы пред-я.
В этих задачах в качестве критериев оптиальности могут выступать прибыль, себестоимость, затраты станочного времени и т.д. Это м\б задача как на макс. так и на мин. В качестве неизвестных выступают объемы прод-ии.
На максимум:
Для
выплаты n видов прод-ии пп-е исп-ет m групп
оборудования. Найти такой план выпуска прод-ии, кот. обеспечивает макс.
прибыли. обозначим ![]() -
кол-во прод-ии j-го вида, выпускаемое по s-тому
технологическому способу. Qj – кол-во технологических способов произ-ва j-го
вида прод-ии.
-
кол-во прод-ии j-го вида, выпускаемое по s-тому
технологическому способу. Qj – кол-во технологических способов произ-ва j-го
вида прод-ии. ![]() -
выражает затраты раб. вр. i-ой группы оборудования при произ-ве ед. прод-ии j-го
вида по s-тому технологическому способу.
-
выражает затраты раб. вр. i-ой группы оборудования при произ-ве ед. прод-ии j-го
вида по s-тому технологическому способу. ![]() - приб.
от реализации ед. прод-ии j-го вида, произведен. по s-тому технолог.
способу. bi – фонд раб. вр. i-ой группы
оборудования.
- приб.
от реализации ед. прод-ии j-го вида, произведен. по s-тому технолог.
способу. bi – фонд раб. вр. i-ой группы
оборудования.
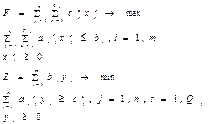
Напр.: n=2, Q1=2,Q2=3
1. оценка yi показывает на сколько возрастает прибыль, если вр. работы i-ой группы оборуд-я возрастает на 1 ед.
2. yi показывает дефицитность i-ой группы оборуд-я. Цем больше yi тем выше дефицитность i-ой группы оборуд-я.
yi в задаче подобного типа наз-ся прокатной оценкой.
Задача на минимум:
Требуется найти оптимальный план выпуска n видов прод-ии из m видов рес-ов, обеспечивающих min себестоимости прод-ии при заданном уровне прибыли.
![]() - объем
рес-а i-го вида
- объем
рес-а i-го вида ![]() -
себестоимость прои-ва прод-ии j-го вида по s-тому технолог. способу. Р- задан.
уровень прибыли.
-
себестоимость прои-ва прод-ии j-го вида по s-тому технолог. способу. Р- задан.
уровень прибыли.
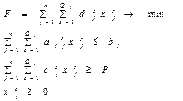
Построим двойственную задачу:
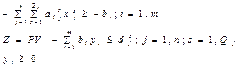
Оценки yi показывают насколько снизится себес-ть всего выпуска прод-ии, если объем i-го рес-са увеличится на 1 ед. Чем более дефицитен ресурс, тем выгоднее наращивать объем.
V имеет смысл оценки задан. уровня прибыли. Она пок-ет на сколько ед. возрастет себестоимость при увеличении задан. уровня прибыли на 1 ед.
29. Задача оптимального исп-я сырья.
Эти задачи эквивалентны моделям оптимального раскроя промыщлен. материалов. Его сущность состоит в разработке таких технологически допустимых раскройных планов, при кот. из стандартной ед. раскраиваемых ресурсов получается комплект заготовок требуемого размера. Критерием оптимальности явл-ся либо мин. общей величины отходов кроя, либо мин. кол-ва раскраиваемых исходных ед. рес-ов. Исходными материалами могут быть какие-либо длинномерные конструкции (трубы, профильный прокат), либо листовые, либо рулонные.
Сформулируем задачу для длинномерного и сводного материалов: Пусть в нашем распоряжении имеется n видов раскроев. Нужно получить m видов заготовок раскраевомого исходного материала. Дано плановое задание по каждому виду заготовок bi. Известна величина aij – выражает кол-во заготовок i-го вида, кот. мы получаем при раскрое ед. исходного материала по j-му варианту раскроя. Сj – объем отхода при раскрое ед. исходного материала по j-му варианту раскроя. Найти кол-во ед. исходного материала, раскраиваемого по каждому из вариантов раскроя с точки зрения обеспечения мин. отходов из заданного уровня объема заготовок каждого вида.
Обозначим через хj – кол-во ед. исходного материала, раскраиваемого по j-му варианту раскроя.
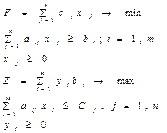
Оценка y*i показывает насколько возрастет объм отходов при увеличении планового задания по выпуску заготовок i-го вида на 1 ед. Т.е. чем больше y*i, тем выгоднее снижать плановое задание по выпуску заготовок i-го вида.
Варианты раскроя находятся на основании след. соотношений:
![]()
li – длина i-го вида заготовок
30. Задача определения наилучшего состава смеси.
Допустим
получаемая смесь должна иметь в своем составе m различных
компонент (ингридиентов) в опр-х кол-ах. Эти компоненты явл-ся при этом
составными частями n исходных материалов. Обозначим через ![]() кол-ва\о
исходного материала j-го вида, входящего в смесь и подлежащего определению.
кол-ва\о
исходного материала j-го вида, входящего в смесь и подлежащего определению. ![]() - цена
материала j-го вида;
- цена
материала j-го вида; ![]() - кол-во
i-го компонента, содержащегося в единице материала j-го
вида;
- кол-во
i-го компонента, содержащегося в единице материала j-го
вида; ![]() -
необходимое кол-во i-го компонента в смеси. Найти такой состав смеси, кот.
обеспечит ее заданные св-ва и стоимость кот-го будет минимальна.
-
необходимое кол-во i-го компонента в смеси. Найти такой состав смеси, кот.
обеспечит ее заданные св-ва и стоимость кот-го будет минимальна.
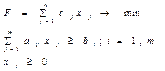
![]() - оценка
i-го компонента смеси показывает насколько возрастает стоимость смси при
увеличении потребности в i-ом компоненте на 1 ед.
- оценка
i-го компонента смеси показывает насколько возрастает стоимость смси при
увеличении потребности в i-ом компоненте на 1 ед.
32. Открытая и закрытая модели транспортной задачи. Вырождение транспорт. зад.
Если ![]() , то
транспортная задача называется задачей закрытого типа, в противном случае, т.е.
, то
транспортная задача называется задачей закрытого типа, в противном случае, т.е.
![]() , -
открытого типа.
, -
открытого типа.
Математическая модель закрытой транспортной задачи: найти наименьшее значение функции
![]()
при ограничениях:
![]()
![]()
Система ограничений транспортной задачи состоит из m+n уравнений с m×n неизвестными.
Математическая модель открытой транспортной задачи примет вид: найти наименьшее значение функции
![]()
при ограничениях:
Если
![]()
![]() ,
,
![]()
Если
![]()
![]() ,
,
![]()
Открытая модель транспортной задачи имеет неканонический вид.
Если число заполненных клеток (Xij ¹ 0) в таблице равно r, то план называется невырожденным, а если это число меньше r, то план вырожденный - в этом случае в некоторые клетки вписывается столько нулей (условно заполненные клетки), чтобы общее число заполненных клеток было равно r.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.