Динамический синтез с использованием запретных зон. Метод динамического синтеза. Построение запретных зон в низкочастотной области, страница 4

3.1.  Учет  нестабильности параметров в статической системе при постоянном входном воздействии

Данный фактор удобнее учитывать, используя аппарат функций чувствительности.

Функция чувствительности u_ji характеризует уход координаты  х_j  при изменении параметра a_i:    .

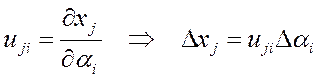Ошибка в статической системе при отработке постоянного входного воздействия, как было получено ранее, 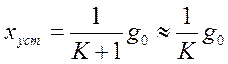  и определяется только величиной К.

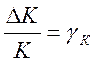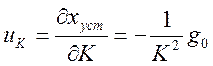При нестабильности коэффициента усиления К:   (относительное изменение К) функция чувствительности ошибки по коэффициенту усиления  . Тогда изменение ошибки вследствие нестабильности коэффициента усиления

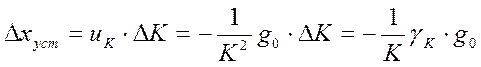, и суммарная ошибка .

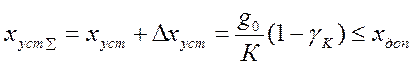В этом случае предельный коэффициент усиления статической системы может быть определен как  .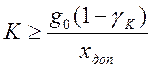

3.2.  Учет нестабильности параметров системы при ограниченном входном сигнале и наличии постоянных возмущений

Рассмотрим систему с единичной обратной связью:

.

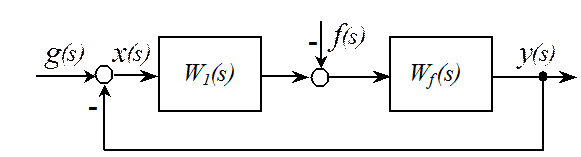
Входной сигнал имеет гармонический характер -  . Установившая ошибка, как было отмечено в п.2, также носит колебательный характер и ее максимальное установившееся значение (максимальная амплитуда) равно

.

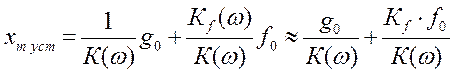Как следует из приведенного выражения, установившаяся ошибка зависит от стабильности коэффициентов усиления . Их относительные изменения 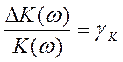  , 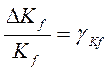. Функции чувствительности соответственно равны 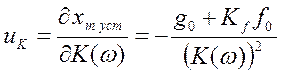, 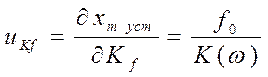. Отклонения  ошибки, вызванные нестабильностью параметров системы, определяются как          ,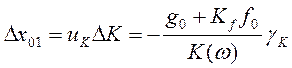

.

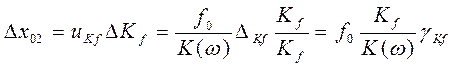Тогда суммарная ошибка в системе с постоянным возмущением и нестабильными параметрами

.

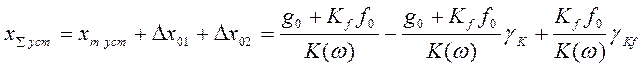Из условия   находится предельный коэффициент усиления системы на частоте ω:  

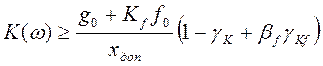, где.

В общем случае, когда относительные отклонения коэффициентов g_i  представляют собой случайные функции и не зависят одна от другой, значение предельного коэффициента усиления системы на частоте ω при отработке входного гармонического сигнала  с ошибкой   равно:      .

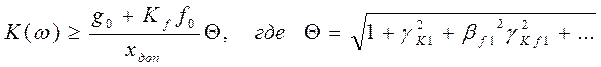Можно рассчитать предельный коэффициент усиления и координаты запретной зоны в зависимости от характера ограничений на входной сигнал. Результаты вычислений сведены в таблицу.

Ограничения на входной сигнал	Предельный коэффициент усиления	Ордината запретной зоны
,
,
,

Запретная зона системы  по точности при наличии постоянных возмущений и ограничений на входное воздействие для общего случая изображена на рисунке.

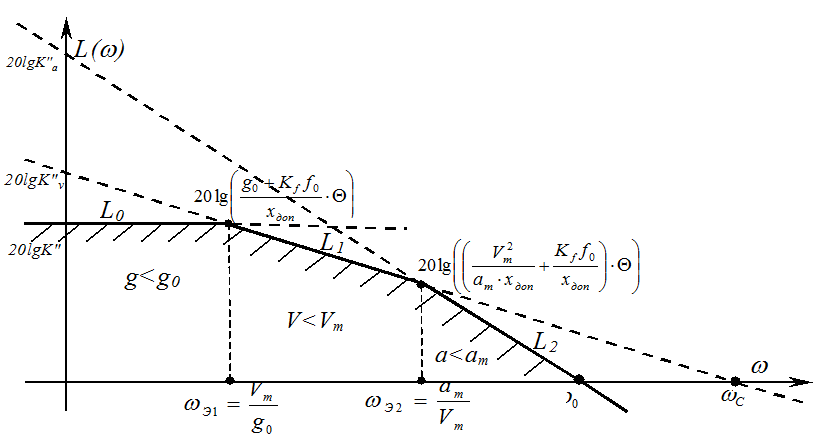          Точки пересечения продолжения участков запретной зоны оси абсцисс находятся, как и ранее, из условий L₂(ω₀)=0 иL₁(ω_С)=0, откуда соответственно получаем:

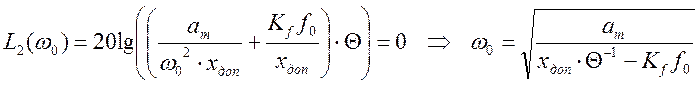    и

 .

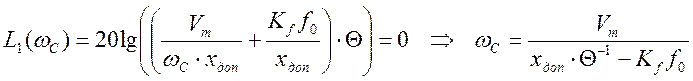Точки пересечения продолжения участков запретной зоны оси ординат находятся из условий 20lgK"_a =L₁(1), 20lgK"_v =L₂(1) и  20lgK" =L₀(1),откуда получаем 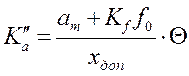 ,  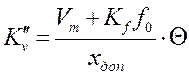и 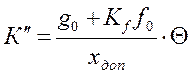 соответственно.

Точки излома запретной зоны (значения абсцисс и ординат их приведены на рисунке) получены из условий L₀(ω_Э1)= L₁(ω_Э1) иL₁(ω_Э2)= L₂ω_Э2).

В реальной системе не все одновременно ограничения на входной сигнал могут иметь место. В этом случае, аналогично п.1.4 и п.2 в запретной зоне будет отсутствовать соответствующий участок. Методика построения запретной зоны в целом и отдельных ее фрагментов также не претерпит изменений.

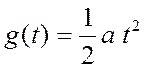Ограничения на входной сигнал вида ,  ,       и    ,   , в настоящем разделе также не рассматривались.  Они являются  частным случаем произвольного входного воздействия при и необходимые значения предельного коэффициента усиления могут быть получены самостоятельно аналогично п.п.1.1, 1.2, 1.3. Практического значения данные коэффициенты не имеют в силу их совпадения с соответствующими координатами запретной зоны.