Динамический синтез с использованием запретных зон. Метод динамического синтеза. Построение запретных зон в низкочастотной области, страница 3

В реальном случае не все одновременно ограничения на входной сигнал могут иметь место. В этом случае в запретной зоне будет отсутствовать соответствующий участок. А методика построения запретной зоны в целом и отдельных ее фрагментов в частности не претерпит изменения.

ЗАМЕЧАНИЕ. Данная методика может быть использована для построения "разрешенной зоны", ниже которой должна быть расположена желаемая ЛАХ системы. В качестве исходных данных используются g_m,, V_m  и  а_{m  -}- предельно допустимые параметры объекта управления, например, двигателя.

2.  Запретная зона по точности  в системе со стабильными параметрами при ограниченном входном сигнале и наличии возмущений

.

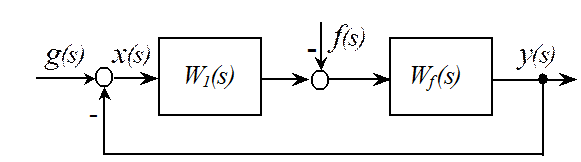
Вне зависимости от характера ограничений на входной сигнал запретная зона строится по методике, описанной в п.1. 

При одновременном воздействии задающего и возмущающего входных сигналов ошибка в системе  является  линейной комбинацией двух составляющих: 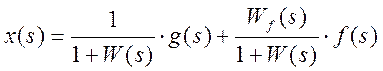 , причем .

Предполагается, что входной сигнал  , причем, при наличии ограничений на скорость изменения и ускорение  будет определяться  как 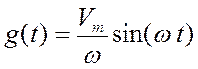 или 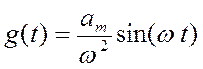 соответственно, как показано в п.1.2 и п.1.3. В любом случае гармонический входной сигнал при постоянном возмущении определит и гармонический характер ошибки с той же частотой.

Ошибка в данной системе (ее максимальное установившееся значение) будет определена как:

.

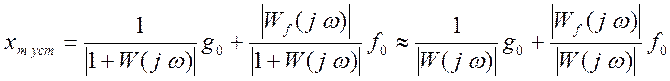Если коэффициент усиления  (постоянный) и требуется, чтобы выполнялось неравенство , то после незначительных преобразований получаем

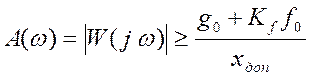, что соответствует предельному коэффициенту усиления системы на частоте ω  при отработке входного гармонического сигнала  с ошибкой .

В зависимости от характера ограничений на входной сигнал можно определить предельный коэффициент усиления и координаты запретной зоны:

Запретная зона системы  по точности при наличии постоянных возмущений и ограничений на входное воздействие для общего случая изображена на рисунке:

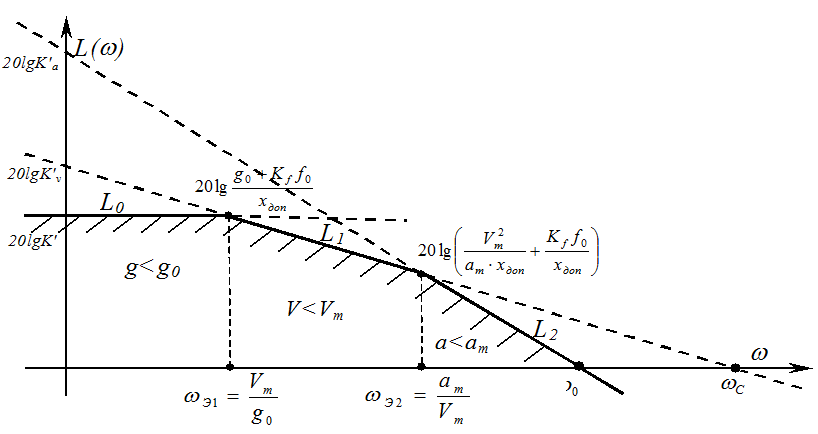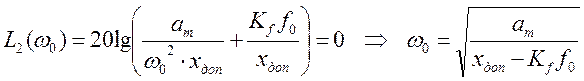          Точки пересечения продолжения участков запретной зоны оси абсцисс находятся, как и ранее, из условий L₂(ω₀)=0 иL₁(ω_С)=0, откуда соответственно получаем:  и .

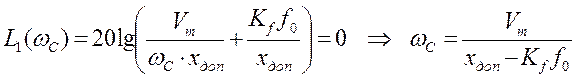Точки пересечения продолжения участков запретной зоны оси и абсцисс находятся, как и ранее, из условий L₂(ω₀)=0 иL₁(ω_С)=0, откуда соответственно получаем:

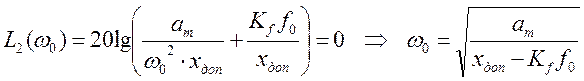 и  .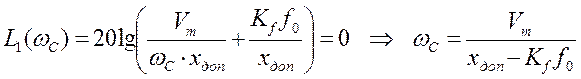

Точки пересечения продолжения участков запретной зоны и оси ординат находятся из условий 20lgK'_a =L₁(1), 20lgK'_v =L₂(1) и  20lgK' =L₀(1),откуда получаем 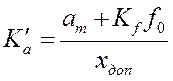 ,  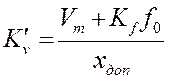и 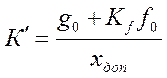 соответственно.

Точки излома запретной зоны (значения абсцисс и ординат их приведены на рисунке) получены из условий L₀(ω_Э1)= L₁(ω_Э1) иL₁(ω_Э2)= L₂ω_Э2).

В реальной системе не все одновременно ограничения на входной сигнал могут иметь место. В этом случае, аналогично п.1.4, в запретной зоне будет отсутствовать соответствующий участок. Методика построения запретной зоны в целом и отдельных ее фрагментов также не претерпит изменений.

Ситуации, когда на входной сигнал наложены ограничения вида ,  ,  и  ,   , в настоящем разделе не рассматривались.  Они являются  частным случаем произвольного входного воздействия при и необходимые значения предельного коэффициента усиления могут быть получены самостоятельно аналогично п.п. 1.1, 1.2, 1.3. Практического значения данные коэффициенты не имеют в силу их совпадения с соответствующими координатами запретной зоны.

3.   Учет  нестабильности параметров