Для того, чтобы система
отработала данный входной сигнал с ограниченной ошибкой, она должна быть
астатической, то есть 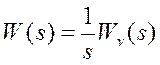 и
и
![]() . Изображение ошибки в
такой системе равно
. Изображение ошибки в
такой системе равно 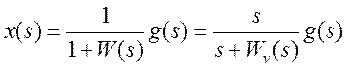 . По теореме
о предельных значениях
. По теореме
о предельных значениях ![]() .
Тогда при
.
Тогда при ![]() (предельный
случай)
(предельный
случай) 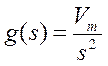 и
и 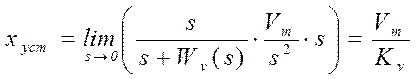 . Отсюда, если потребовать
. Отсюда, если потребовать ![]() , можно получить значение
граничного коэффициента усиления системы
, можно получить значение
граничного коэффициента усиления системы 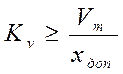 .
.
Из
передаточной функции разомкнутой системы 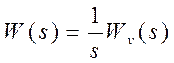 получаем последовательно
частотные характеристики:
получаем последовательно
частотные характеристики:
АФЧХ - 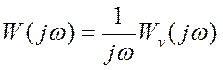 , АЧХ -
, АЧХ - 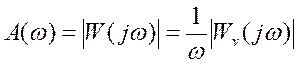 , и
, и 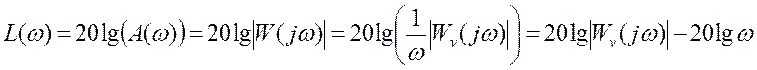 - ЛАХ системы. При
- ЛАХ системы. При ![]() полученная ЛАХ асимптотически
стремится к прямой
полученная ЛАХ асимптотически
стремится к прямой ![]() с
наклоном
с
наклоном 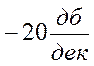 ,
пересекающей ось ординат в точке
,
пересекающей ось ординат в точке 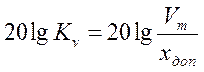 .
.
Аналогично предыдущему
случаю асимптота ![]() является
множеством точек (коэффициентов усиления системы на частоте ω), когда при отработке гармонического
сигнала
является
множеством точек (коэффициентов усиления системы на частоте ω), когда при отработке гармонического
сигнала ![]() , скорость
изменения которого
, скорость
изменения которого ![]() не превышает
не превышает ![]() , установившаяся ошибка не превосходит
, установившаяся ошибка не превосходит
![]() .
.
Покажем истинность
данного утверждения. Так как ![]() ,
то
,
то ![]() . Отсюда
. Отсюда 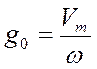 и
и 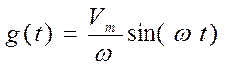 . Установившаяся ошибка при
гармоническом входном сигнале также имеет гармонический характер, причем амплитуда
ее
. Установившаяся ошибка при
гармоническом входном сигнале также имеет гармонический характер, причем амплитуда
ее
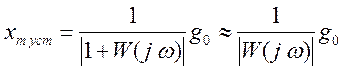 , где
, где ![]() - коэффициент усиления системы
на частоте
- коэффициент усиления системы
на частоте 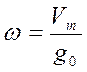 . Тогда из
условия
. Тогда из
условия ![]() получаем,
что
получаем,
что 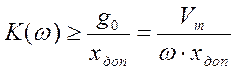 и запретная зона
будет определяться выражением
и запретная зона
будет определяться выражением 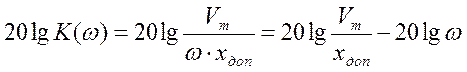 ,
что полностью совпадает с уравнением прямой, полученной выше.
,
что полностью совпадает с уравнением прямой, полученной выше.

1.3.
Обеспечение заданной точности по
входному воздействию при ограничениях ![]()
Как и ранее, рассмотрим режим 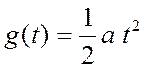 ,
, ![]() .
.
Для того чтобы система
отработала данный входной сигнал с ограниченной ошибкой, она должна обладать
свойством астатизма второго порядка, то есть 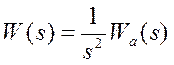 и
и ![]() .
.
Изображение
ошибки в такой системе равно 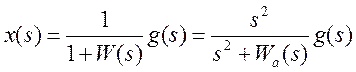 .
По теореме о предельных значениях
.
По теореме о предельных значениях ![]() .
Тогда при
.
Тогда при 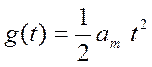 (предельный
случай)
(предельный
случай) 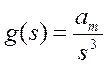 и
и 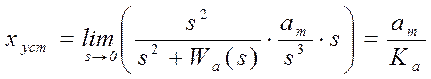 . Отсюда, если потребовать
. Отсюда, если потребовать ![]() , можно получить значение
граничного коэффициента усиления системы
, можно получить значение
граничного коэффициента усиления системы 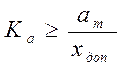 .
.
Из
передаточной функции разомкнутой системы 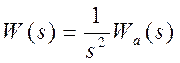 получаем последовательно
частотные характеристики:
получаем последовательно
частотные характеристики:
АФЧХ - 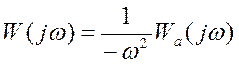 , АЧХ -
, АЧХ - 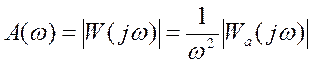 , и
, и 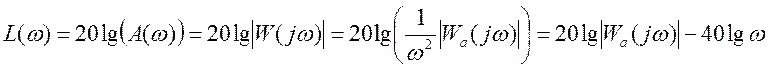 - ЛАХ системы. При
- ЛАХ системы. При ![]() полученная ЛАХ асимптотически
стремится к прямой
полученная ЛАХ асимптотически
стремится к прямой ![]() с
наклоном
с
наклоном ![]() , пересекающей
ось ординат в точке
, пересекающей
ось ординат в точке 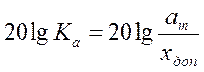 .
.
Аналогично предыдущему
случаю данная линия является множеством точек (коэффициентов усиления системы
на частоте ω), когда при отработке
гармонического сигнала ![]() ,
ускорение которого
,
ускорение которого ![]() не превышает
не превышает ![]() , установившаяся ошибка не
превосходит
, установившаяся ошибка не
превосходит ![]() .
.
Покажем
истинность данного утверждения. Так как ![]() , то
, то ![]() . Отсюда
. Отсюда 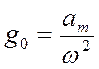 и
и 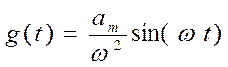 . Установившаяся ошибка при
гармоническом входном сигнале также имеет гармонический характер, причем
амплитуда ее
. Установившаяся ошибка при
гармоническом входном сигнале также имеет гармонический характер, причем
амплитуда ее
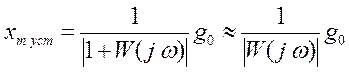 , где
, где ![]() - коэффициент усиления системы
на частоте
- коэффициент усиления системы
на частоте 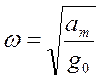 . Тогда из
условия
. Тогда из
условия ![]() получаем,
что
получаем,
что 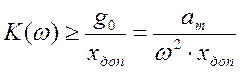 и запретная зона
будет определяться выражением
и запретная зона
будет определяться выражением 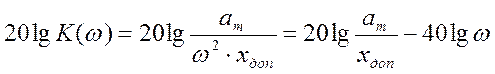 ,
что полностью совпадает с уравнением прямой, полученной выше.
,
что полностью совпадает с уравнением прямой, полученной выше.

1.4. Общий случай ограниченного входного сигнала
Рассматривается
ситуация, когда на входное воздействие одновременно наложены ограничения: ![]()
![]() ,
, ![]() .
.
Из п.п. 1.2 и 1.3 следует, что требование отработки с заданной погрешностью входного воздействия, ограниченного по скорости или ускорению, равносильно обеспечению требуемой точности при отработке входного сигнала меньшей амплитуды.
Так, если
ограничена скорость изменения ![]() ,
то это равносильно отработке гармонического сигнала
,
то это равносильно отработке гармонического сигнала 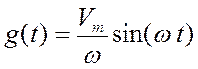 с погрешностью
с погрешностью ![]() . А случай
. А случай ![]() соответствует отработке воздействия
соответствует отработке воздействия
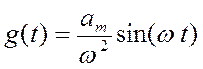 с тем же требованием.
с тем же требованием.
Таким образом,
последовательно накладывая ограничения на входной сигнал, можно получить
запретную зону, изображенную на рисунке. 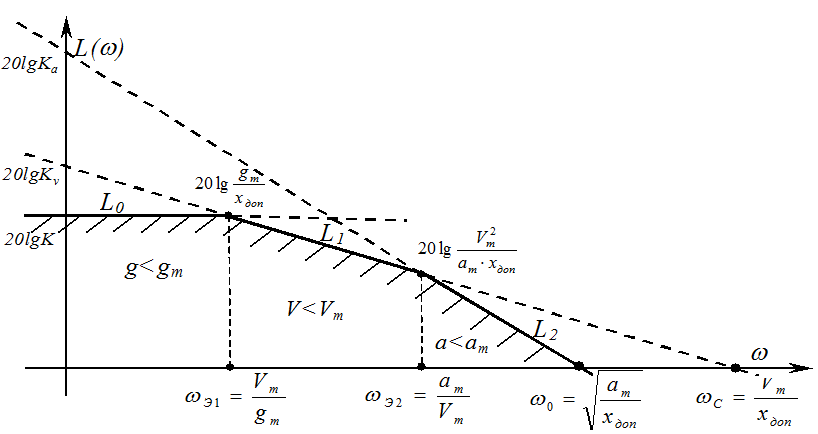 Запретная зона состоит из трех
участков, каждый из которых построен с учетом соответствующих ограничений на
входное воздействие. Дополнительно показаны значения точек пересечения линий
продолжения участков запретной зоны осей абсцисс и ординат. Так, из условия L2(ω0)=0
или
Запретная зона состоит из трех
участков, каждый из которых построен с учетом соответствующих ограничений на
входное воздействие. Дополнительно показаны значения точек пересечения линий
продолжения участков запретной зоны осей абсцисс и ординат. Так, из условия L2(ω0)=0
или 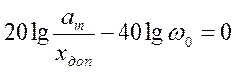 , получаем
, получаем 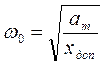 . Из условия L1(ωС)=0 или
. Из условия L1(ωС)=0 или
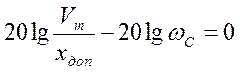 , получаем
, получаем 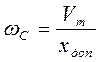 . Общие точки (точки излома
запретной зоны) найдены из условий L0(ωЭ1)=
L1(ωЭ1)
иL1(ωЭ2)= L2ωЭ2). (Вычисления рекомендуется
выполнить самостоятельно).
. Общие точки (точки излома
запретной зоны) найдены из условий L0(ωЭ1)=
L1(ωЭ1)
иL1(ωЭ2)= L2ωЭ2). (Вычисления рекомендуется
выполнить самостоятельно).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.