Классический анализ переходных процессов в RC – цепях 1-го порядка. Графики напряжения на конденсаторе

Задача 6.19                                                                   Выполнил студент группы

РТ5-04 :

Классический анализ переходных

процессов в RC – цепях 1-го порядка.

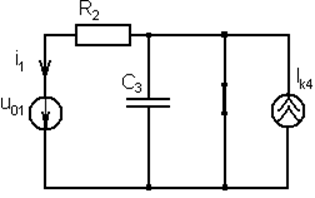
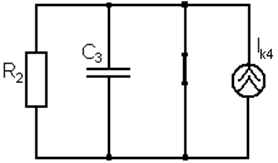
Записать выражение тока i₁(t) источника напряжения цепи после коммутации и построить его график, если 

В

R₂ = 100 Ом , С₃ = 10 мкФ ,I_k4= 4A

Решение данной задачи проведём методом наложения последовательно расчитав токи i₁^’(t) от действия источника напряжения u₀₁(t) и ток i₁^’’(t) от действия источника тока I_k4.

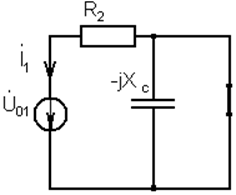
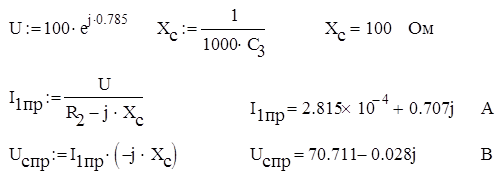1 .После  коммутации ток конденсатора и ток резистора одинаковы и равны                                                                 i₁^’(t)  Расчитаем этот ток по комплексной схеме замещения методом комплексных амплитуд.

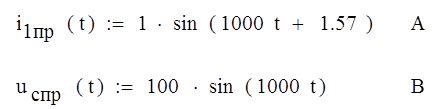Перейдем от комплексных амплитуд к временным зависимостям принужденной составляющей напряжения на конденсаторе u_c^’(t) и принужденной составляющей тока i₁^’(t).

Найдём значение напряжения u_c^’(0-). Очевидно что оно равно 0, т.к. конденсатор до коммутации был закорочен.

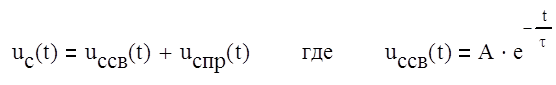Временную зависимость u_c^’(t),будем искать в виде

τ – электро – магнитная постоянная времени, которую можно найти по формуле :

Где R_{в х} –входное сопротивление схемы, относительно зажимов конденсатора, из которой исключены все источники.

Очевидно что R_вх = R₂ ,тогда τ=1∙10^-3 с

Постоянную интегрирования А найдем из начальных исловий

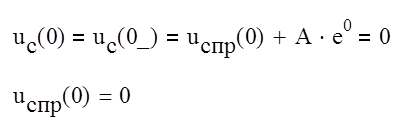Напряжение на конденсаторе скачком измениться не может и в момент коммутации равно тому значению непосредственно предшествующему коммутации.

Отсюда находим А. Очевидно что А = 0 , следовательно в цепи сразу возникнет установившийся процесс.

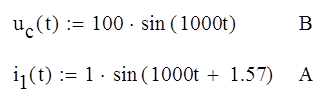Запишем выражение для напряжения конденсатора :

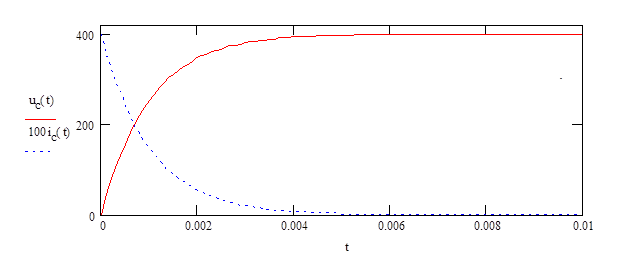
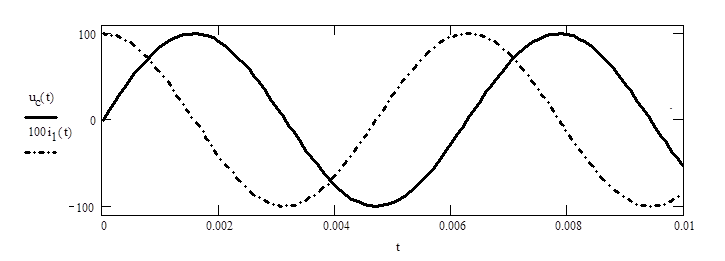Графики напряжения на конденсаторе u_c^’(t) и тока i₁^’(t)

2 .Расчитаем принужденную составляющую напяжения на конденсаторе.

Очевидно что оно равно падению напряжения на резисторе :

U_cпр^’’= R₂ ∙I_k4 = 100 ∙ 4 = 400 В

Напряжение на конденсаторе до коммутации равно :

u_c^’’(0-) = 0 B

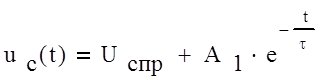Функцию напряжения на конденсаторе будем искать в виде:

τ была найдена в п.1

Постоянную интегрирования А₁ найдем из начальных условий

u_c^’’(0-) = u_c^’’(0) = U_cпр^’’+A₁ = 0

A₁ = -U_cпр^’’= -400 В

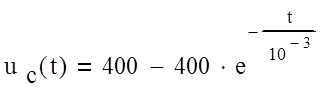Запишем выражение для напряжения конденсатора

В

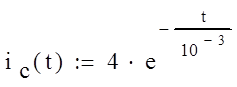Запишем выражение для тока конденсатора

А

i₁^’’(t) = I_k4 – i_c^’’(t)

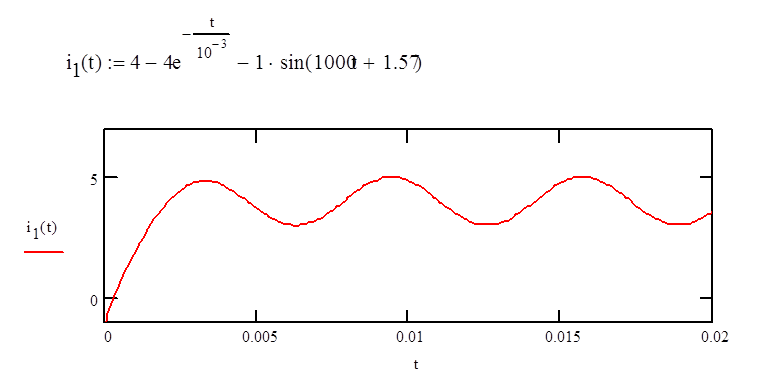3. Запишем выражение для искомого тока i₁(t) = i₁^’’(t) – i₁^’(t)