Сигналы и их характеристики. Функция включения Хевисайда. Математическая модель сигнала. Временной график сигнала

1.Сигналы и их характеристики

1.1.  Сигнал определяется восьмизначным равномерным кодом согласно варианту и подварианту (табл. 1), где символ «0» соответствеует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 0.1 мкс.

                                                               Таблица 1

Вариант	Подвариант
	8
5	01010010

    1.2.   Требуется:

●   Записать математическую модель сигнала в виде линейной комбинации функций Хевисайда, построить временной график.

Функция включения Хевисайда (рис.1) определяется выражением: 

       

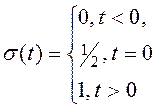
                                                                                  Рис.1.1. Функция включения Хевисайда

Математическая модель сигнала, представляющая собой линейную комбинацию функций включения, имеет следующий вид:

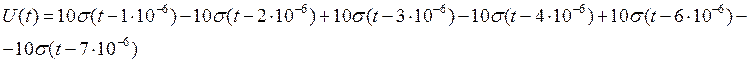
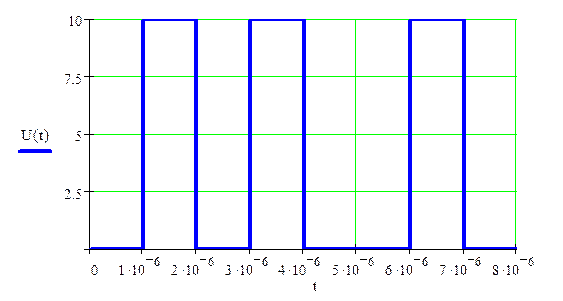Временной график сигнала:

Рис.1.2. Временной график сигнала

·  Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму.

Базис, составленный из функций Уолша, является ортонормальным базисом для . Функции Уолша привлекли внимание благодаря простоте их генерирования при помощи переключательных схем. Функции Уолша определяются при помощи рекуррентного соотношения:

где - нормированное время. 

Для наглядности выполняемых расчетов на графиках представим результат перемножения исходного сигнала на соответствующую функцию Уолша для первых 8 функций:

 0)  

Рис.1.3. Результат перемножения исходного сигнала на 0-ую функцию Уолша

Спектральные коэффициенты (коэффициенты разложения сигнала в базисе Уолша) определяются как:

где  - исходный сигнал, - k-ая функция Уолша.

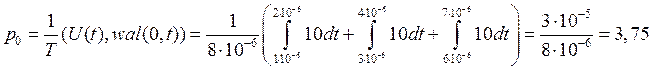
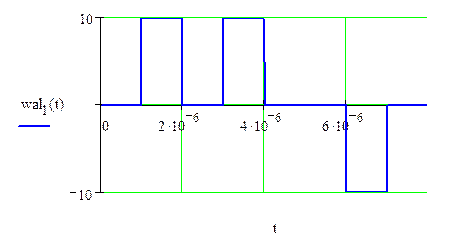1)  

Рис.1.4. Результат перемножения исходного сигнала на 1-ую функцию Уолша

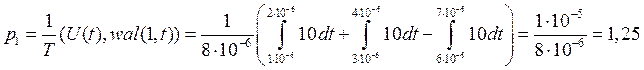
2)  

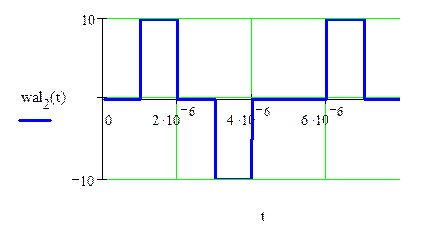
Рис.1.5. Результат перемножения исходного сигнала на 2-ую функцию Уолша

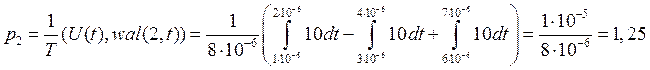
3)  

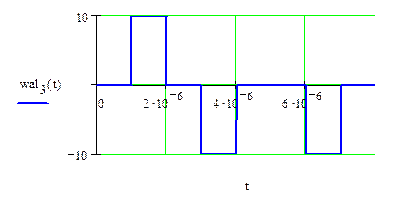
Рис.1.6. Результат перемножения исходного сигнала на 3-ую функцию Уолша

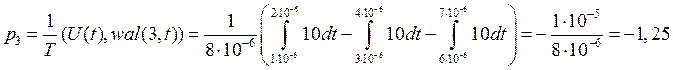
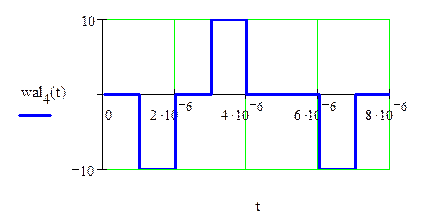4)  

Рис.1.7. Результат перемножения исходного сигнала на 4-ую функцию Уолша

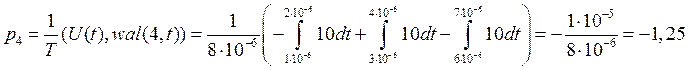
5)  

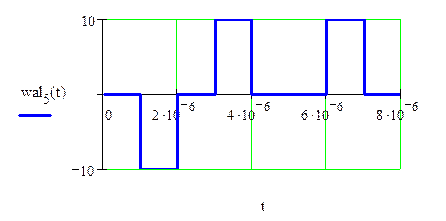
Рис.1.8. Результат перемножения исходного сигнала на 5-ую функцию Уолша

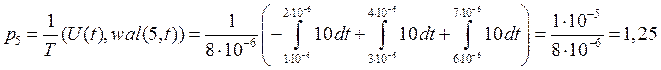
6)  

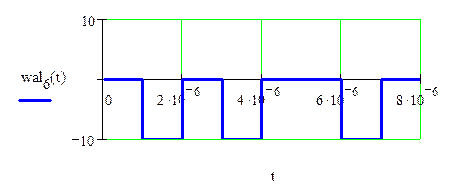
Рис.1.9. Результат перемножения исходного сигнала на 6-ую функцию Уолша

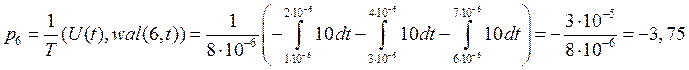
7)  

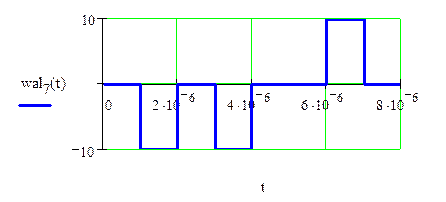
Рис.1.10. Результат перемножения исходного сигнала на 7-ую функцию Уолша

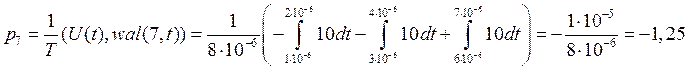
Спектральная диаграмма разложения исходного сигнала в базисе Уолша:

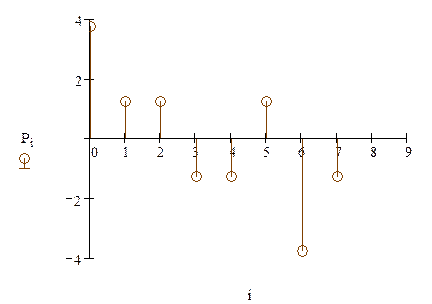
Рис.1.11. Спектральная диаграмма

·  Найти спектральную плотность сигнала относительно ядра Фурье, построить графики её модуля и аргумента.

Вместо ряда, т.е. суммы бесконечного счетного множества базисных функций, умноженных на спектральные коэффициенты для представления сигналов можно использовать интеграл от функции 2-х переменных (которая представляет собой как бы несчетное множество базисных функций), умноженный на функцию одной переменной, называемой спектральной плотностью.  

Очень часто для представления сигналов используется базисное ядро Фурье  . Ядро является самосопряженным т.к.

Поэтому спектральная плотность сигнала  относительно данного ядра определяется выражением:

известным как преобразование Фурье.

Значение спектральной плотности прямоугольного импульса находится по формуле:

где - амплитуда импульса, - длительность импульса.

Спектральная плотность смещенного прямоугольного импульса определяется по свойству преобразования Фурье, называемого теоремой сдвига:

где - задержка импульса.

Определим длительность и задержку каждого из элементов исходного сигнала:

Длительность импульсов: , ,

Задержка импульсов: , ,

Таким образом, функция спектральной плотности для данного сигнала имеет вид:

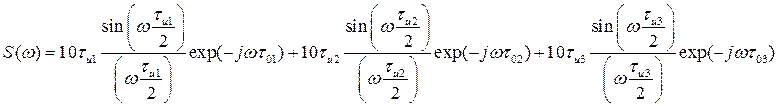
Используя математический пакет MathCAD, построим графики модуля