Основы теории двухполюсников. Классификация двухполюсников. Понятие входной функции реактивных двухполюсников

Лекция № 1

Основы теории двухполюсников. Классификация двухполюсников.

Понятие входной функции реактивных двухполюсников

Любая электрическая цепь, рассматриваемая относительно каких-либо двух её зажимов, называется двухполюсником.

Классификация двухполюсников

1.  Линейные и нелинейные двухполюсники;

2.  Одноэлементные, двухэлементные и многоэлементные двухполюсники;

3.  Реактивные двухполюсники (РД) и двухполюсники с потерями;

4.  Активные и пассивные двухполюсники.

Введем понятие эквивалентности двухполюсников. Два двухполюсника, имеющие разную структуру, эквивалентны в электрическом смысле, если их сопротивления или соответственно проводимости равны друг другу во всём спектре частот. Замена в электрической цепи какого-либо двухполюсника эквивалентным ему двухполюсником не влияет на токи или напряжения в остальной части электрической цепи. Это положение справедливо как для установившегося, так и для переходного процесса.

В дальнейшем мы будем рассматривать только реактивные двухполюсники (РД) – двухполюсники, содержащие только реактивные элементы.

Зависимости сопротивлений или проводимостей двухполюсников от частоты называются частотными характеристиками. Частотные характеристики двухполюсников, образующих электрическую цепь, предопределяют частотные свойства данной цепи, т.е. зависимости амплитуд и фаз токов или напряжений от частоты.

Термином, обобщающим входные сопротивления  и проводимость  реактивных двухполюсников, является входная функция . Входную функцию  можно реализовать в виде электрической цепи с сосредоточенными параметрами при условии, что она является дробно-рациональной.

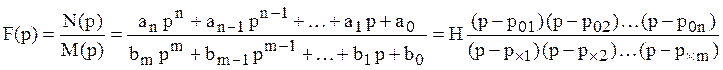, где  – const,  – множитель уровня,

 – нули,  – полюсы входной функции.

Не всякой функции  можно поставить в соответствие линейный пассивный двухполюсник, составленный из элементов с положительными вещественными параметрами. Необходимое и достаточное условие физической реализуемости рациональной функции  в качестве операторной входной функции линейной пассивной цепи заключается в том, чтобы  являлась положительной вещественной функцией комплексной частоты .

Введем понятие положительной вещественной функции. Это такая функция , которая удовлетворяет двум условиям:

• её вещественная часть положительна при положительных значениях вещественной части p:

 (условие положительности)

• её мнимая часть равна нулю при мнимой части , равной нулю:

 (условие вещественности)

Непосредственно по последним двум выражениям трудно определить является ли заданная функция  положительной вещественной функцией частоты , поэтому обычно проверяют выполнение следующих условий, которые полностью вытекают из этих выражений:

1.  Все коэффициенты  и  полиномов  и  должны быть вещественны и неотрицательны;

2.  Наибольшие и соответственно наименьшие степени полиномов  и  не могут отличаться более чем на единицу;

3.  Нули  и полюсы  функции  не могут располагаться в правой части комплексной полуплоскости, в противном случае не выполняются условия устойчивости цепи.

4.  Нули  и полюсы  функции , расположенные на мнимой оси, должны быть только простыми (некратными), причём производные функции  в нулях и вычеты в полюсах должны быть вещественны и положительны.

5.  Вещественная часть функции  должна быть неотрицательной на мнимой оси, т.е.

.

Пример № 1. Определим, являются ли функции

, ,

положительными вещественными функциями комплексного переменного .

Непосредственно по виду функции устанавливаем, что функция  не удовлетворяет первому условию (коэффициент ), а функции  и  не удовлетворяют второму условию (разности наивысших степеней числителя и знаменателя функции  и наименьших степеней числителя и знаменателя функции  превышают единицу). Следовательно, данные функции не являются положительными вещественными функциями.

Пример № 2. Определим, являются ли функция

положительной вещественной функцией комплексного переменного , либо является ли она физически реализуемой в качестве операторной входной функции линейной пассивной цепи.

Непосредственно по виду функции  устанавливаем, что все коэффициенты полиномов  и  вещественны и положительны, а наибольшие и наименьшие степени этих полиномов отличаются на единицу. Выполним проверку третьего условия:

Все нули функции , т.е. , , откуда , .

Все полюсы функции , т.е. , , откуда , , .

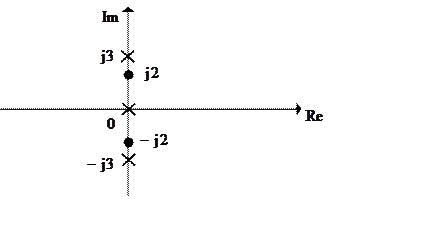Видно, что нули и полюсы не располагаются в правой части комплексной полуплоскости, однако они располагаются на мнимой оси и являются простыми, т.е.

Требуется выполнить проверку четвёртого условия. Для этого определим производные функции  в нулях и вычеты  в полюсах.

Производные функции в нулях:

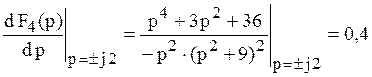
Из теории функции комплексного переменного известно, что вычет функции  по полюсу первого порядка равен:

.

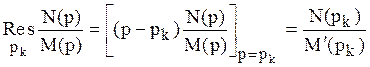Тогда вычеты в полюсах:, .

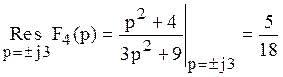Четвёртое условие полностью выполняется.

Выполним проверку последнего пятого условия: .

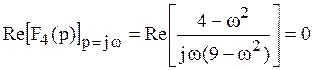 – условие выполняется.

Вывод:  является вещественной положительной функцией.

Одноэлементные и двухэлементные реактивные двухполюсники

Индуктивность и ёмкость представляют собой одноэлементные реактивные двухполюсники.

Комплексное сопротивление индуктивного элемента во всем спектре частот имеет положительный знак, а комплексная проводимость – отрицательный знак:

, .

Комплексное сопротивление ёмкостного элемента во всем спектре частот имеет отрицательный знак, а комплексная проводимость – положительный знак:

, .

Представим частотные характеристики указанных величин.

 

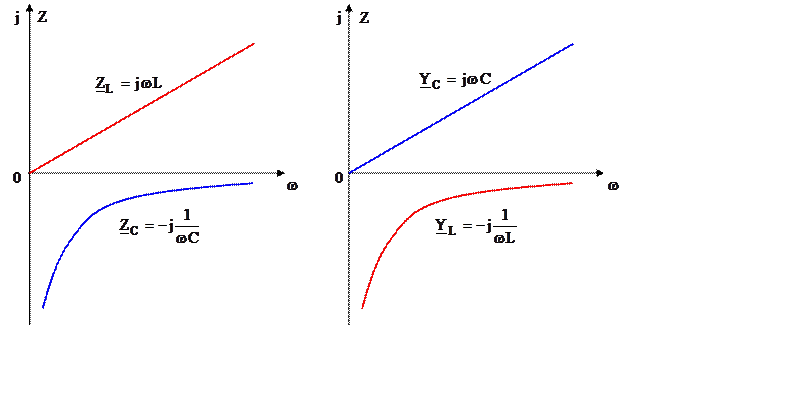Из графиков видно, что  соответствуют . Следует отметить, что как сопротивления, так и проводимости двухполюсников с ростом частоты возрастают, т.е.

, .

Последнее выражение определяет одно из общих свойств реактивных двухполюсников.

Данные двухполюсники называются дуальными. Запишем условие дуальности реактивных двухполюсников. Пусть , .