Переходный ток на входе цепи. Выбор схемы и строки данных. Расчёт принуждённого режима. Схема замещения для расчёта принуждённого режима

Задание

Найти переходный ток на входе цепи, изображенной на схеме и построить график его изменения в функции времени. ЭДС источника задана в виде .

1.  Принужденную составляющую тока находить методом комплексных амплитуд (т.е. символическим методом), а свободную – операторным.

2.  Если наибольшее значение свободной составляющей окажется несоизмеримо мало по сравнению с амплитудой принужденной составляющей, то допускается раздельное построение этих составляющих на чертеже в разных масштабах (без суммирования).

1. Выбор схемы и строки данных

Выбор рабочей схемы и строки исходных данных производится в соответствии с формулами:

номер схемы  .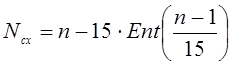

номер строки данных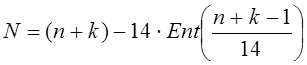

где n— номер студента в списке группы, k—номер группы, Ent(x)—целая часть числа х. Подставляя в эти формулы n=12 и k=7, получим

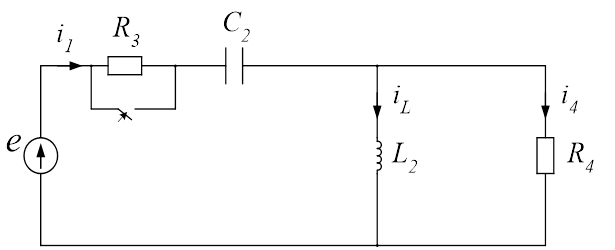
Рис.1. Рабочая схема

2. Расчёт принуждённого режима (t=∞)

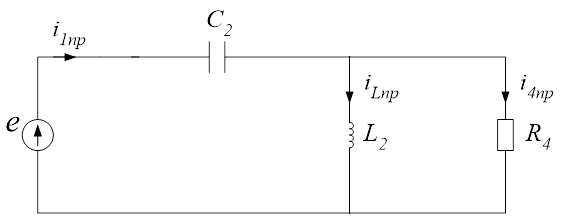
Рис.2. Схема замещения для расчёта принуждённого режима

В соответствии с рабочим заданием, расчёт будем вести методом комплексных амплитуд. Для упрощения записёй в данном пункте опустим индекс пр в обозначении комплексных амплитуд (напр. ).

 

. 

.  

,   .

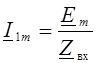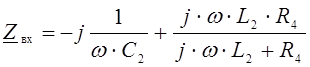По формуле делителя тока: .  .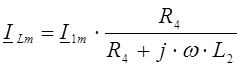

.

По первому закону Кирхгофа: .  

.

.  .   .

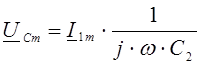Запишем выражения для мгновенных значений в принуждённом режиме:

.

.

.

.

3. Расчёт режима до коммутации (t<0)

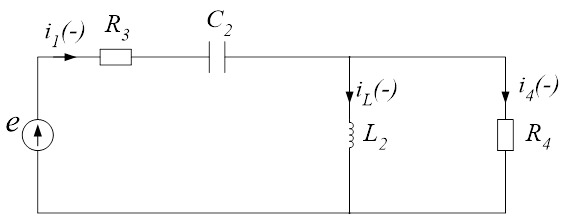
Рис.3. Схема замещения для расчёта режима до коммутации

Расчёт режима до коммутации будем вести методом комплексных амплитуд. Для упрощения записёй в данном пункте опустим символ (−) в обозначении комплексных амплитуд (напр. ).

.

.  

,   .

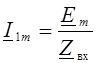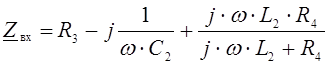По формуле делителя тока: .  .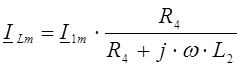

.

По первому закону Кирхгофа: .   .

.

.  .   .

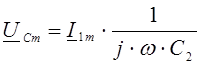Запишем выражения для мгновенных значений в режиме до коммутации:

.

.

.

.

4. Определение независимых начальных условий (t=0)

По законам коммутации:  и .

.

.

.  .

Определим начальные условия для свободных составляющих:

;    ;   .

;  ;  .

5. Определение свободной составляющей входного тока операторным методом

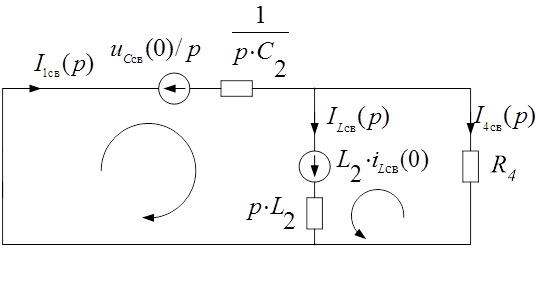
Рис.4. Операторная схема замещения

Ток  можно определить по методу контурных токов, сделав его контурным.

.    .

.

.

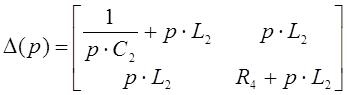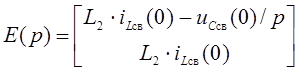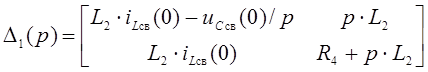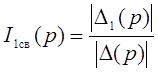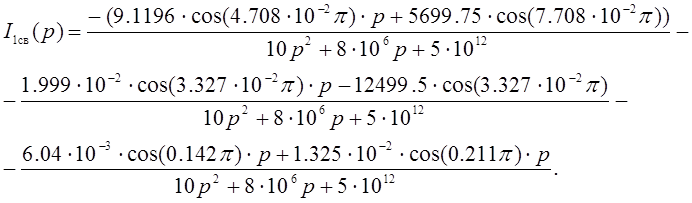
Чтобы найти , нужно к функции  применить обратное преобразование Лапласа.

.

6. Построение графика входного тока

Выражение для входного тока выглядит следующим образом:

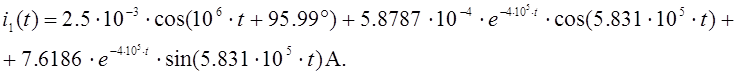
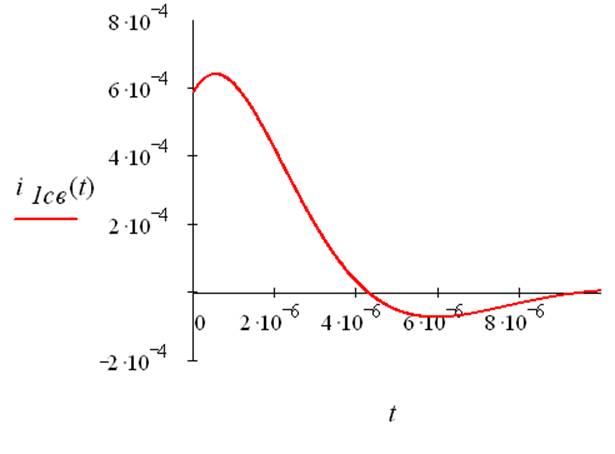
Рис.5. График свободной составляющей входного тока

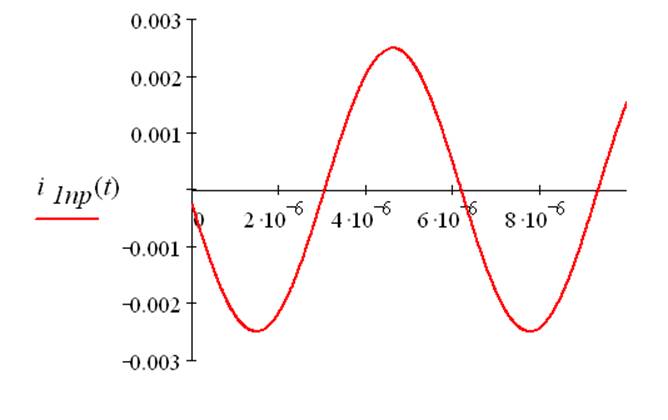
Рис.6. График принуждённой составляющей входного тока

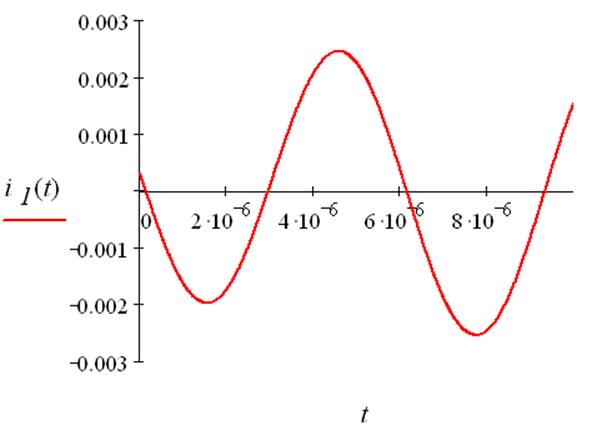
Рис.7. График входного тока

7. Проверка полученного результата

Проверку полученного результат можно выполнить, сравнив значения входного тока в определённый момент времени, вычисленные разными способами. Удобнее всего вычислить значения в момент времени .

Определим ток  как зависимое начальное условие.

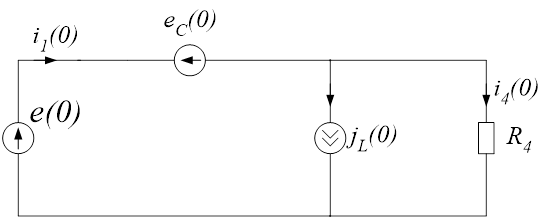
Рис.8. Схема замещения для определения зависимых начальных условий

.   . .

По первому закону Кирхгофа: .

По второму закону Кирхгофа: .

.

.

.

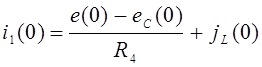Подставим в выражения для входного тока, полученное в пункте 6, значение времени .

.  

.  

Можно проверить корни характеристического уравнения . Судя по выражению для свободной составляющей входного тока, корни этого уравнения равны: .

Составим характеристическое уравнение:

.   .   .

;

;

;

;

.

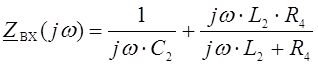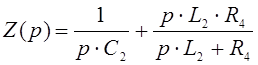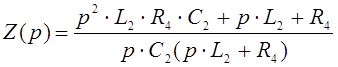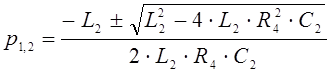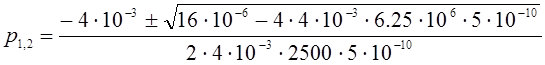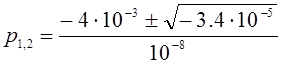Результаты, полученные разными способами, совпадают. Следовательно, можно сделать вывод о точности расчётов.