Лестничные LC – фильтры. Частотные зависимости ослабления, фазы и характеристические сопротивления. Собственные сопротивления фильтров

Лекция № 6

Лестничные LC – фильтры

Лестничные LC – фильтры – это фильтры из каскадно соединенных Г, Т и П-образных реактивных четырехполюсников.

 

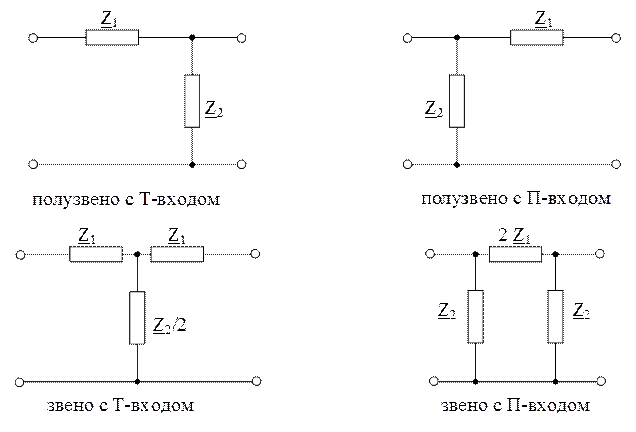Ранее было показано, что собственная мера передачи звеньев Т и П типа определяется:

, где .

С другой стороны:.

Поскольку Z₁ и Z₂ реактивные сопротивления, то, .

В полосе пропускания (ПП) ослабление равно нулю, поэтому , .

В полосе задерживания (ПЗ) ослабление отлично от нуля, следовательно , .

Для определения граничных частот ПП выполняются условия , .

В (ПП) т.к. , то , отсюда следует , .

Из последнего неравенства следует, что реактивные сопротивления в (ПП) не могут быть одного знака, т.е. одно из них имеет индуктивный характер, другое – емкостной.

Преобразуем последнее неравенство ,  , получим:

,  – эти два уравнения определяют частоты среза.

В полосе задерживания , т.е.  принимает значения , поэтому

, .

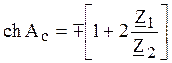Фильтры нижних частот (ФНЧ) типа «к».

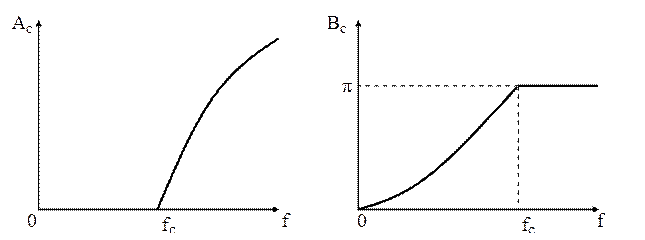
Частотные зависимости ослабления, фазы и характеристических сопротивлений

Для фильтров типа «к» выполняется условие: , где k – вещественное число, не зависящее от частоты, следовательно, двухполюсники Z₁ и Z₂ являются обратными. Рассмотрим ФНЧ типа «к». Г-образное полузвено, Т и П-образные звенья этого фильтра представим в следующем виде:

 

Для этих фильтров: , . Произведение сопротивлений: .

 – номинальное сопротивление фильтра.

Определим граничные частоты полосы пропускания из уравнений: , .

Первая граничная частота ПП , т.к. , .

Вторая граничная частота ПП , т.к.

, , откуда

Полоса пропускания (ПП) находится в диапазоне частот: .  – частота среза.

В (ПП) собственное ослабление фильтра , а собственная фаза определяется выражением:

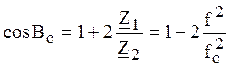. (фаза изменяется от 0 до π)

 

Собственные сопротивления фильтров изменяются с частотой:

, .

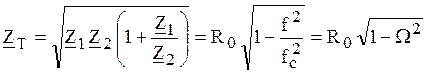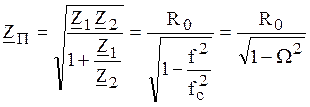Построим графики частотной зависимости собственных сопротивлений.

 

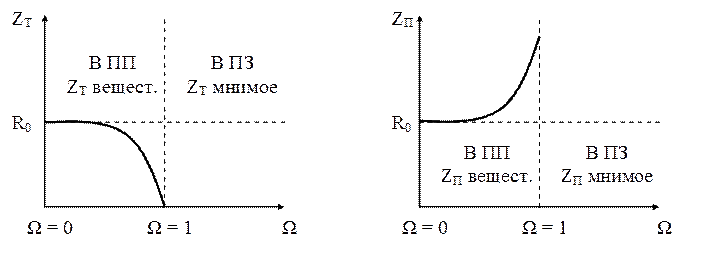Фильтры верхних частот (ФВЧ) типа «к».

Частотные зависимости ослабления, фазы и характеристических сопротивлений

 

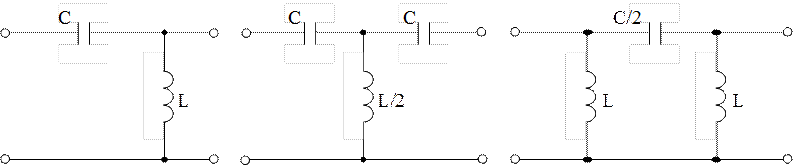Для этих фильтров: , . Произведение сопротивлений: .

Определим граничные частоты ПП.

Первая граничная частота ПП получается из выражения: , т.е.

, откуда .

Вторая граничная частота ПП получается из выражения: , т.е.

, , откуда

Полоса пропускания (ПП) находится в диапазоне частот: .  – частота среза.

В (ПП) собственное ослабление фильтра , а собственная фаза определяется выражением:

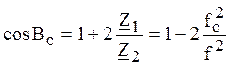. (изменяется от –π до 0)

Построим соответствующие графики:

 

Собственные сопротивления фильтров изменяются с частотой:

, .

 

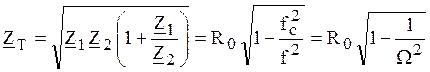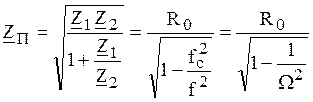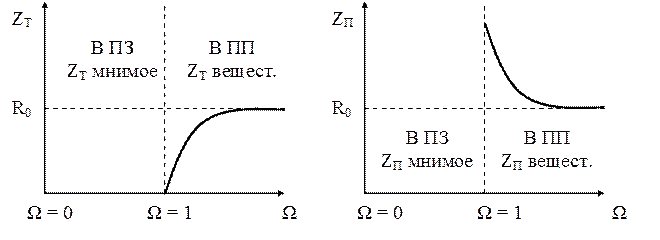Полосовые фильтры (ПФ) типа «к».

Частотные зависимости ослабления, фазы и характеристических сопротивлений

 

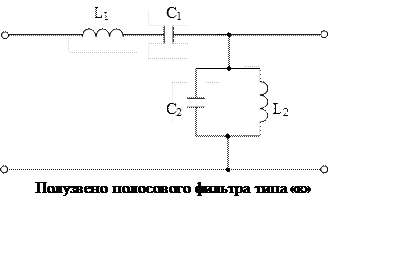Рекомендуется самостоятельно построить Т и П-образные звенья полосового фильтра типа «к».

Для нашего фильтра имеем:

, .

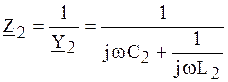Определим произведение этих сопротивлений:

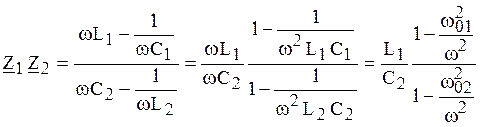, где , .

 при условии, что  или .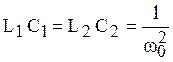

В этом случае данный ЧП является полосовым фильтром типа «к», т.к. .

Откуда .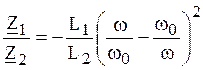

Из равенства следует, что  и  разного знака. Это необходимо, чтобы ЧП был фильтром.

Определим граничные частоты полосы пропускания из условий: , .

Эти условия, безусловно, можно записать в виде: , .

Для определения граничных частот получаем два уравнения:

, .

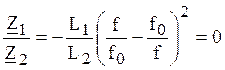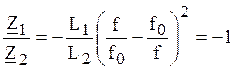После алгебраических преобразований:

, , .

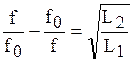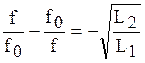Из последних двух равенств определяем:

, .

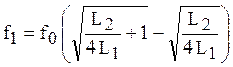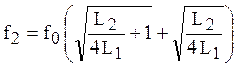Частотные зависимости ослабления и фазы:

 

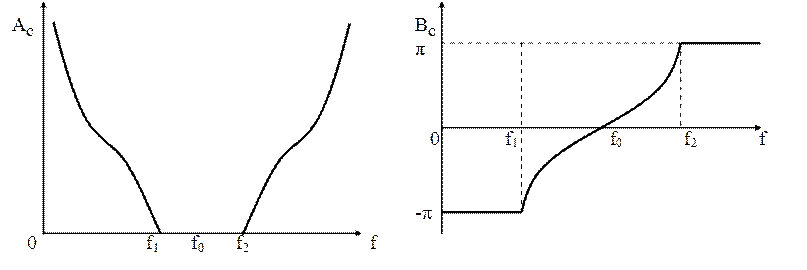 – центральная частота.

Две полосы пропускания в диапазоне частот:  и .

Две полосы задерживания в диапазоне частот:  и .

Частотные зависимости характеристических сопротивлений:

, .

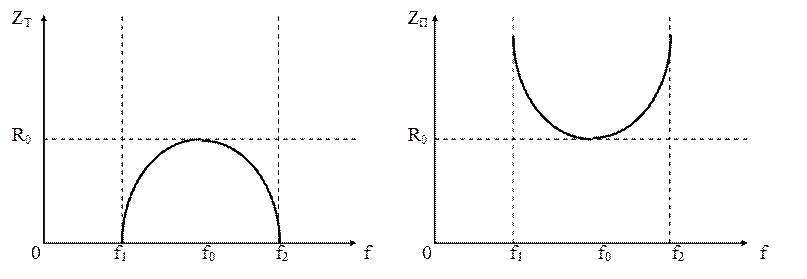
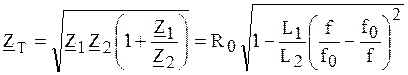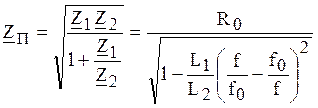Заграждающие фильтры (ЗФ) типа «к».

Частотные зависимости ослабления, фазы и характеристических сопротивлений

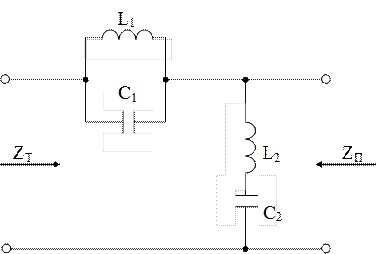Представим полузвено ЗФ типа «к».

Рекомендуется самостоятельно построить Т и П-образные звенья ЗФ типа