Анализ импульсной схемы с использованием средств вычислительной техники. Матрица параметров цепи

17.  Лабораторная работа № 26

АНАЛИЗ  ИМПУЛЬСНОЙ  СХЕМЫ

С  ИСПОЛЬЗОВАНИЕМ  СРЕДСТВ  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Цель работы

Ознакомиться с реализацией численного метода анализа переходных процессов в цепях первого порядка.

Схемы и исходные данные к лабораторной работе № 25

Объект и средства исследования

Методом переменных состояния рассчитывается схема с импульсным воздействием в соответствии с заданным вариантом. Численный анализ выполняется методом Рунге-Кутта.

Рабочее задание

1. В соответствии со своим вариантом расчётного задания записать уравнение состояния при .

2. Составить уравнение для определения искомого тока или напряжения.

3. Составить подпрограмму вычисления значения функции воздействия .

4. Ввести в программу ...

5. ... рассчитать ...

6. Результаты вычислений занести в таблицу, аналогичную таблице контрольного примера.

7. На одном графике построить кривые входного воздействия и рассчитанной величины.

8. *⁾ Результаты численного анализа искомой величины сопоставить с результатом её аналитического расчёта при помощи интеграла Дюамеля.

__________________________

*⁾ Выполняется факультативно в порядке научно-исследовательской работы.

Методические указания и рекомендации

Согласно законам теории цепей переходный процесс в электрической цепи с конечным числом сосредоточенных линейных двухполюсных элементов при  описывается системой  независимых линейных обыкновенных дифференциальных уравнений при известных  начальных значениях напряжений на конденсаторах и токов через катушки**⁾. Эти величины называются переменными состояния цепи.

__________________________

*⁾ Предполагается, что в цепи нет ни одного сечения, состоящего только из катушек и источников тока, и ни одного контура, содержащего только конденсаторы и источники напряжения.

Рассмотрим алгоритм формирования "вручную" уравнений для вычисления переменных состояния - уравнений состояния.

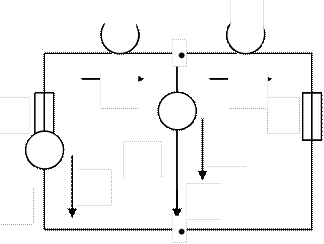
Считая известными мгновенные значения токов катушек и напряжений на конденсаторах и опираясь на принцип компенсации*⁾, изобразим схему замещения заданной цепи для произвольного момента времени .

__________________________

*⁾ Любой элемент цепи с известным значением тока или напряжения может быть эквивалентно заменён соответственно источником тока или напряжения известного значения.

 

Рис.26.1                                                       Рис.26.2

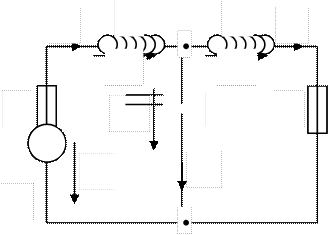
Например, для схемы цепи, показанной на рис.26.1, в результате описанной замены получим схему замещения, как на рис.26.2. Затем записываем систему выражений для мгновенных значений напряжений на всех катушках и токов через все конденсаторы. В рассматриваемом случае искомые выражения, записанные по законам Кирхгофа, выглядят следующим образом:

 ;

 ;

 .

И, наконец, сокращая первое уравнение на , второе - на , а третье - на , получаем систему уравнений состояния, записанную в нормальной форме (форме Коши):

 ;

 ;

 .

В общем случае уравнения могут быть записаны в матричной форме

 , где   и  - векторы переменных состояний и воздействий,

,             ,

 и  - число энергоёмких элементов и источников, соответственно,  и  - матрицы параметров цепи,

,             .

Если известны  и  для любого , то последующие состояния цепи определяются однозначно.

Вектор  значений величин, не совпадающих с переменными состояния, находятся как линейная комбинация векторов переменных состояния и воздействий:

 .

Если  - число искомых величин , то

,       ,         .

Численное решение уравнения первого порядка вида

при  и заданном значении .

Приближённые дискретные значения  искомой переменной при  определяются последовательно с шагом , начиная от момента времени , для которого известно . Искомые значения находятся по методу Рунге-Кутта второго порядка:

 , где  ;                     .

Тогда   .

Примечание:  1. Программой предусмотрена возможность вычисления с пропуском  последовательных значений искомых функций. В таких случаях в            необходимо ввести число .

2. По завершении очередного шага вычислений можно изменить значения  и , а также (при необходимости) и подпрограмму ....