Проверка гипотезы о нормальности закона распределения экспериментальных данных, страница 2

6)  Вычисление средне-квадратичного отклонения

7)  Нахождение теоретического числа данных в интервале

8)  Вычисление  и заключение вывода о нормальности закона распределения заданной последовательности

 

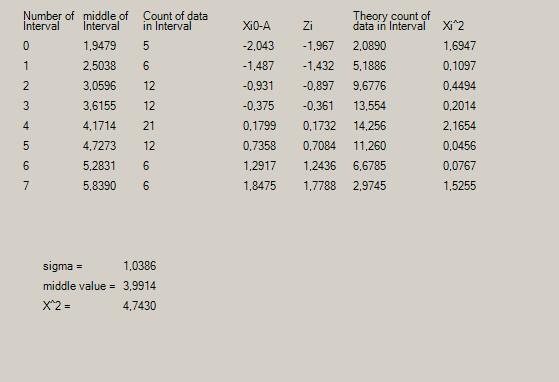
Разбиваем всю совокупность на интервалы,  для n = 80 рекомендуемое число интервалов 7-9, примем r = 8; Вычисляем h = 0.5559.

Вычисляем среднее арифметическое значение A = 3.9914.

Вычисляем = 1.0386;

Так как мы не проводили совмещение интервалов, то число степеней свободы будет f = 7 - 1 = 6;

Уровень значимости возьмем q = 0.1;

Из таблицы распределения   найдем  =  1,64 и  = 12,59

Для заданной последовательности  = 4.7430

Так как 1,64 < 4.7430 < 12.59, гипотеза о нормальности закона распределения принимается.

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Text;

using System.Windows.Forms;

namespace SystModel_2_002

{

    public partial class Form1 : Form

    {

        double[] arr;       // input array

        double n;           // lenght of the input array

        double r;           // count of the Interval

        double[,] inter;    // intervals

        double min, max;    // minimem and maximum number in the array

        double step;        // step of the interval

        double[] midInter;  // middle of the interval

        double[] dataC;     // count of number in the interval

        double mid;         // middle number of the array

        double X0_A;        // summary of Xi0-A

        double sigma;       // sigma

        double[] Xi0_A;     // Xi0-A