Расчет на прочность надрессорной балки грузового вагона. Схема приложения расчетных сил к надрессорной балки тележки и положение расчетных сечений

4 Расчет на прочность надрессорной балки грузового вагона

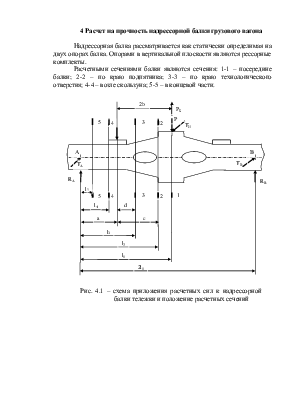
Надрессорная балка рассматривается как статически определимая на двух опорах балка. Опорами в вертикальной плоскости являются рессорные комплекты.

Расчетными сечениями балки являются сечения: 1-1 – посередине балки; 2-2 – по краю подпятника; 3-3 – по краю технологического отверстия; 4-4 – возле скользуна; 5-5 – в концевой части.

Рис. 4.1 – схема приложения расчетных сил к надрессорной балки тележки и положение расчетных сечений

4.1 Определение расчетных сил действующих на балку

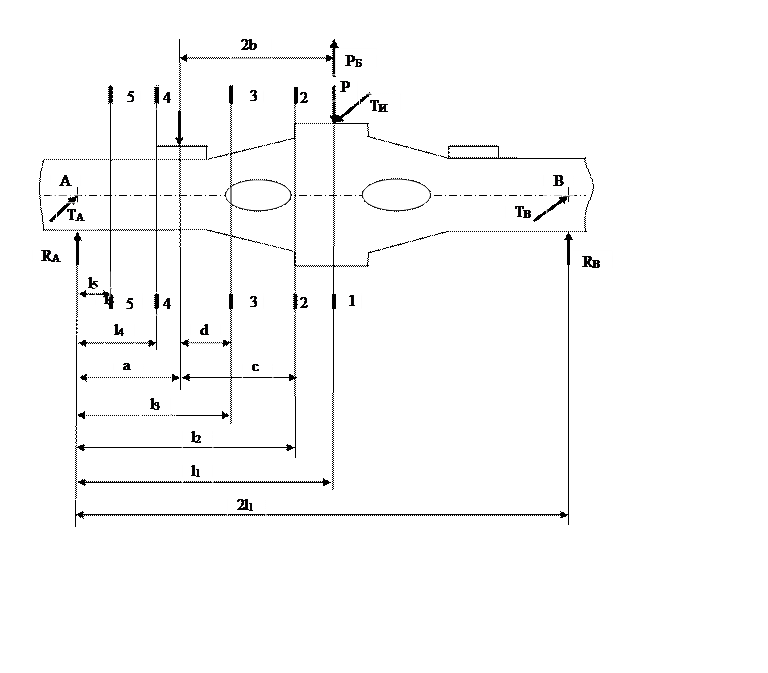
Расчетными силами при проектировании надрессорной балки являются: вертикальная статическая Р_ст; вертикальная динамическая Р_д; вертикальная от боковых сил Р_Б; вертикальная от продольных сил инерции при торможении Р_И; продольная сила инерции, возникающая при торможении Т_И. Горизонтальная сила от боковых нагрузок, действующая вдоль надрессорной балки, в расчете не учитывается.

Вертикальная статическая сила, кН,

                                          (4.1)   где  Р_БР – вес вагона брутто, кН,

                                           Р_БР = m₀p₀;                           (4.2)

где m₀ – осность вагона, m₀ = 4;

р₀ – заданная осевая нагрузка, р₀ = 230 кН;

Тогда

Р_БР = 4·230 = 920 кН.

где n_T – число 2-осных тележек в вагоне, n_т = 2;

n_нб – число надрессорных балок  тележки,  n_нб = 1;

m_КП – масса колесной пары, m_КП = 1254 кг;

m_Б – масса буксового узла, m_Б = 0,74 кг;

m_рп – масса рессорного подвешивания, m_рп=40 кг;

m_р – масса рамы тележки, m_р=363 кг;

g – ускорение свободного падения, g = 9,81 м/с²;

Тогда

 кН,

Вертикальная динамическая сила, кН,

                                               Р_Д=Р_СТК_Д,                           (4.3)

где К_Д – коэффициент вертикальной динамики,

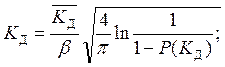                                                      (4.4)

где  – среднее значение К_Д,

                                                  (4.5)

где  – коэффициент, принимаемый равным 0,1 для   обрессоренных частей тележки;

 – коэффициент, учитывающий влияние числа осей "n₀" в тележке,

                                                                    (4.6)

Тогда

где  – скорость движения вагона в соответствии с принятым расчетным режимом. Для III режима дня грузовых вагонов  = 33 м/с;

 – статический прогиб рессорного подвешивания, м. Для тележек грузовых вагонов,  = 0,05 м;

 – параметр функции распределения. Для грузовых вагонов            = 1,13;

Р(К_Д) – доверительная вероятность, Р(К_Д) = 0,97.

Тогда среднее значение

значение коэффициента

;

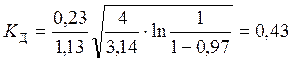по формуле (5.3)

Р_Д = 430·0,43 = 185  кН.

Вертикальная составляющая от боковых сил, кН,

                           (4.7)

где H_Ц – центробежная сила от веса вагона брутто, кН,

                                              H_Ц  = _ЦּР_ст;                          (4.8)

H_Ц  = 0,075·430 = 32,3кН, где _Ц – коэффициент, учитывающий центробежную силу. Для грузовых вагонов, _Ц  = 0,075;

Н_В – давление ветра на кузов вагона, кН,

H_В = w F;                                          (4.9)

где w – удельное давление ветра, w = 0,5 кН/м²;

F – площадь боковой проекции кузова на вертикальную продольную плоскость симметрии вагона, F=6 м²;

H_В =0,5 · 6 = 3 кН, где h_Ц, h_В – вертикальные расстояния от точки приложения силы Р_Б до точек приложения сил Н_Ц и Н_В соответственно, h_Ц=1,500 м, h_В=2,500м;

2b – расстояние между осями скользуна и подпятника, 2b =  0,762 м.

Тогда

 кН.

Продольная сила инерции при торможении, кН

Т_и = ּР_бр,                                               (4.10)

где – коэффициент, принимаемый равным 0,2 – при нормальных и повышеннах скоростях движения и отсутсвии соударения.

Т_и = 0,2·920 = 184кН.

Вертикальная от продольных сил инерции

 кН

В горизонтальной плоскости расчетной силой является Т_и, а в вертикальной плоскости:

при движении по прямому участку пути

Р = Р_ст + Р_д + Р_И = 430 + 184 + 42,3 = 656,3 кН;

при движении в кривой – Р и Р_Б.

4.2  Изгибающие моменты в сечениях балки

При движении вагона по прямому участку пути:

– в вертикальной плоскости

М_Вi = R_A∙l_i                                                                            (4.11)

– в горизонтальной плоскости

М_Гi = Т_A∙l_i                                                   (4.12)

где l_i – расстояние от точки приложения реакции R_А до рассматриваемого i-го сечения: l₁=1,018 м,  l₂=0,826 м, l₃=0,528 м,  l₄=0,218 м,  l₅=0,102  м, a=0,256 м, c=0,572 м, d=0,342 м, 2b=0,702 м.

R_A, Т_А – соответственно вертикальная и горизонтальная реакции в опоре А балки на рессорный комплект, кН;

R_A = 0,5 ∙ Р = 0,5∙656,3 = 328,2 кН.

Т_A = 0,5∙Т_И = 0,5∙184 = 92кН.

Тогда по формуле (4.11)

М_В1 = R_A∙l₁ = 328,2 ∙1,028 = 337,4 кНּм;

М_В2 = R_A∙l₂ = 328,2  ∙0,826 = 271,1 кНּм;

М_В3 = R_A∙l₃ = 328,2  ∙0,598 = 196,3 кНּм;

М_В4 = R_A∙l₄ = 328,2  ∙0,218 = 71,5 кНּм;

М_В5 = R_A∙l₅ = 328,2  ∙0,102 = 33,5кНּм.

По формуле (4.12)

М_Г1 = Т_A∙l₁ = 92∙1,028 = 95,4 кНּм;

М_Г2 = Т_A∙l₂ = 92∙0,826 = 76,6кНּм;

М_Г3 = Т_A∙l₃ = 92∙0,598 = 55,5 кНּм;

М_Г4 = Т_A∙l₄ = 92∙0,218 = 20,2 кНּм;

М_Г5 = Т_A∙l₅ = 92∙0,102 = 9,5 кНּм.

При движении вагона по кривому участку пути:

– в вертикальной  плоскости

М_В1=R_A∙l₁ - Р_Б(l₁ - a)=328,2∙1,028 – 45,6(1,018 - 0,256)=302,6 кНּм

М_В2=R_A∙l₂ - Р_Б(l₂ - a)= 328,2∙0,826 – 45,6 (0,826 - 0,256)=245,1 кНּм

М_В3=R_A∙l₃ - Р_Б(l₃ - a)= 328,2∙0,598 – 45,6 (0,598 - 0,256)=180,6 кНּм

М_В4=R_A∙l₄ - Р_Б(l₄ - a)= 328,2∙0,218 – 45,6 (0,218 - 0,256)=73,3 кНּм

М_В5=R_A∙l₅ - Р_Б(l₅ - a)= 328,2∙0,102 – 45,6 (0,102 - 0,256)=40,4 кНּм

– в горизонтальной плоскости – изгибающие моменты останутся такими же что и при движении по прямому участку пути, т.е. М_Гi=Т_A∙l_i.

4.3  Определение геометрических характеристик расчетных сечений надрессорной балки с использованием ЭВМ

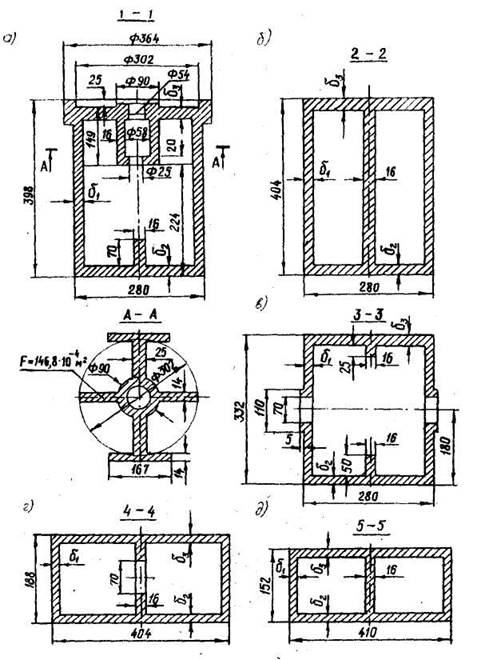
Рис 4.2 – Расчетные сечения надрессорной балки тележки грузового вагона с осевой нагрузкой Р₀<245 кН

Линейные размеры расчетных сечений для осевых нагрузок 220-244 кН приведены в таблице 4.1.

Таблица 4.1 – Линейные размеры расчетных сечений

Расчет геометрических характеристик выполняем с помощью программы на ЭВМ разработанной на кафедре “Вагоны”, результаты вычислений сводим в таблицу 4.1.

Таблица 4.1 – Геометрические характеристики сечений надрессорной балки тележки модели 18-100 грузового вагона

4.4 Вычисление напряжений в расчетных сечениях балки и сравнение их с допускаемыми

Данная надрессорная  балка  изготовлена из стали марки 20ГФЛ