Математические модели локомотивов в расчетах на ЭВМ. Понятие математической модели. Этапы математического моделирования

предметного моделирования принципиально отличается идеальное моделирование, которое основано не на материальной аналогии объекта и модели, а на аналогии идеальной, мысленной.

Идеальное моделирование носит теоретический характер. Различают два вида идеального моделирования: интуитивное и знаковое.

Под интуитивным понимают моделирование, основанное на интуитивном представлении об объекте исследования, не поддающемся формализации либо не нуждающемся в ней. Так жизненный опыт каждого человека можно считать его интуитивной моделью окружающего мира.

Знаковым называют моделирование, использующее в качестве моделей знаковые преобразования какого-либо вида: схемы, графики, чертежи, формулы, наборы символов и т.д., а также включающее совокупность законов, по которым можно оперировать с выбранными знаковыми образованиями и их элементами.

Важнейшим видом знакового моделирования является математическое моделирование, при котором исследование объекта осуществляется посредством модели, сформулированной на языке математики с использованием тех или иных математических методов. 

Моделирование как способ познания, получило особенно широкое распространение с внедрением в практику научных исследований ЭВМ. Большие возможности вычислительных машин позволили существенно расширить рамки математического моделирования, сущность которого заключается в решении сложных и громоздких систем уравнений или логических задач, описывающих поведение изучаемого объекта и его модели.

Задача решается посредством формализации (детерминированной или вероятностно-статистической) основных свойств объекта процессов и явлений. Варьируя параметрами модели можно определить влияние отдельных параметров на свойства реальных изучаемых объектов, наглядно наблюдать изменения этих свойств в выбранном масштабе времени. Машинное моделирование применяют в тех случаях, когда непосредственное исследование или натурное (физическое) моделирование невозможно или нецелесообразно.

При моделировании необходимо обосновать аналогию между моделью и реальным физическим явлением и только на этой основе результаты, полученные на модели, переносят на изучаемое явление. Без этого обоснования моделирование теряет познавательное значение, перестает быть достоверным источником информации о реальных явлениях.

В математическом моделировании в отличие от других форм моделирования предполагается замена объекта его математическим описанием. Правомерность такой замены и качество принимаемых по результатам моделирования решений связаны с понятием адекватности модели. Обычно говорят, что модель адекватна объекту, если результаты моделирования находят прямое или косвенное практическое подтверждение и, таким образом, могут служить основой для прогнозирования свойств изучаемых объектов. При этом адекватность модели зависит как от цели моделирования, так и от принятых критериев оценки его результатов.

Пусть на ЭВМ необходимо смоделировать некоторый процесс. Для этого предварительно проводят его математическое описание или,  иначе говоря, строят его математическую модель. Далее математическую модель используют для программирования на ЭВМ,  получая, таким образом, ее "машинную копию",  т.е. вычислительную модель. Реализация на ЭВМ вычислительной модели дает результаты, которые оценивают и переносят на моделируемый процесс. В виде объекта изучения можно представить и весь процесс, и отдельные его составляющие.

При математическом моделировании процессов обычно используют системный подход, когда объект моделирования с одной стороны рассматривается как элемент, решающий самостоятельную задачу и связанный с другими элементами, а с другой - как сложная система, которая может быть представлена как совокупность других более простых процессов и явлений. Состояние объекта моделирования может быть описано некоторым множеством размерных величин x₁, x₂, ... , x_n, y₁, y₂, ... , y_m, a₁, a₂, ... , a_k, ... , a_p. Целесообразно  разделить эти величины на две группы: переменные процесса x_i, y_i (числовые значения которых в ходе процесса могут меняться) и параметры a_k,  которые в данном процессе постоянны, но могут иметь другое значение в аналогичных процессах. В свою очередь, переменные процесса могут быть условно разделены на входные x_i и выходные y_i. Определение конкретного вида соотношения между входными и выходными переменными для данного процесса

                                                 (1.1)

в частности, и является одной из задач моделирования. Для решения этой задачи предварительно необходимо знать:

- перечень переменных, которыми с достаточной полнотой характеризуется изучаемый объект;

- необходимую степень детализации уравнений (или точности решения).

Пример

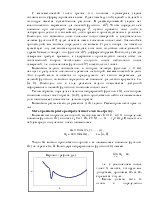
Расход топлива грузовым тепловозом за поездку определяется выражением